初中数学5.1函数与它的表示法精品课件ppt

这是一份初中数学5.1函数与它的表示法精品课件ppt，共20页。PPT课件主要包含了水位和时间，≤x≤21，图像法，表示函数关系的方法，1图象法，2列表法，3解析法，列表法，解析法，图象法等内容，欢迎下载使用。

你还记得什么是函数吗？
在现实生活中，函数关系是处处存在的。你知道表示函数关系的方法通常有哪几种吗？
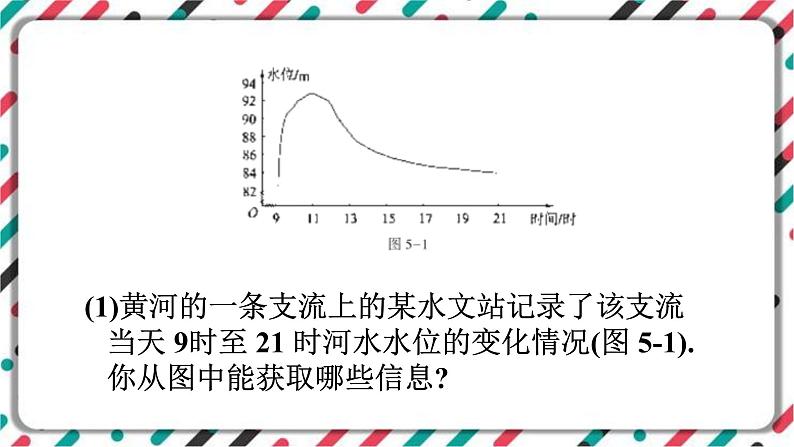
(1)黄河的一条支流上的某水文站记录了该支流当天 9时至 21 时河水水位的变化情况(图 5-1).你从图中能获取哪些信息?
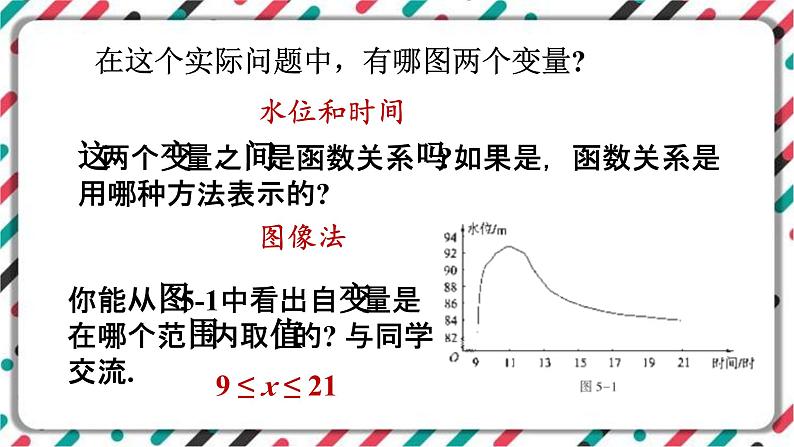
在这个实际问题中，有哪图两个变量?
这两个变量之间是函数关系吗?如果是，函数关系是用哪种方法表示的?
你能从图5-1中看出自变量是在哪个范围内取值的? 与同学交流.
在这个实际问题中，弹簧长度y与拉力x之间是函数关系吗? 如果是，函数关系是用哪种方法表示的?其中，自变量是在哪个范围内取值的?
（2）一根弹原长 15 cm，在弹一端所受到的拉力不超过 40 N的弹性限度内，每增加10N的拉力，弹簧就伸长 2 cm，请你填写下表:
在这个实际问题中，物体距地面的高度h 与物体下落的时间t之间是函数关系吗?如果是，它们之间的函数关系是用哪种方法表示的?其中，自变量是在哪个范围内取值的?
（3）物体从 490 m的高度处自由下落，物体距地面的高度h(m)与物体下落的时间t(s)之间的关系满足表达式h=490-4.9t2 .
（1）用数学式子表示函数的方法叫做解析法
（2）用表格表示函数关系的方法叫做列表法
（3）用图象表示函数关系的方法叫做图象法
用来表达函数关系的数学式子叫做函数解析式或函数关系式
上述的例子中，（1）（2）（3）分别是哪种表示函数的方法呢？
用描点法画函数图象时用到了函数关系的哪几种表示方法？
不能准确由自变量的值确定函数值
由自变量的值直接查出函数值
只能表示出自变量的有限个离散值及其函数值，不易发现趋势
全面、准确、方便，自变量在可取值范围内的每一个值都可以通过表达式求出它的函数值
不够形象直观，并不是每一个函数都可以写出它的解析式
如图 5-2,它的图象是以A(0,15)和B(40,23)为端点的一条线段.由此可设函数的表达式为y= kx + 15(k是常数，0(5)利用问题(2)表中给出的数据，画出y与x的函数图象你发现弹管的长度y是拉力x的一次函数吗?为什么?写出y与x的表达式.
将x=40，y=23代入上式，得23 = 40k + 15.解得 k=所以这个函数的表达式为y =x + 15 (0 ≤ x ≤ 40)
根据函数的表达式和自变量可以取值的范围，列出下面的表格:
(6)你会用描点法画出问题 (3) 中的函数图象吗?由问题(3)的实际意义和函数表达式h=490-4.9t2先确定自变量t可以取值的范围是0≤t ≤10.
以时间t为横轴、高度h为纵轴画出直角坐标系(根据该问题的实际背景，横轴和纵轴选取不同的单位长度 )，然后以上表中的每一个有序实数对 (t，h) 为坐标，在直角坐标系中描出相应的各点，用一条平滑的曲线按自左向右的顺序顺次连接它们，便得函数h=490-4.9t2 （ 0≤t ≤10 ）的图象它是一段曲线(图5-3).
1.一辆汽车在一段行驶过程中，速度v随行驶时间t变化的情况如图所示.(1)在这个问题中，速度v与行驶时间t之间的函数关系是用哪种方法表示的?
(2)这个过程中汽车共行驶了多少分钟?在哪个时间段内，汽车行驶速度最大?最大速度是多少?
(3)在哪个时间段内汽车的行驶速度逐渐增加?在哪个时间段内行驶速度逐渐减少?在哪个时间段内汽车按匀速运动行驶?按匀速运动行驶时，速度是多少?
当0≤t≤10、 20≤t≤40时， v逐渐增加；
当80≤t≤100时， v逐渐减少；
当10≤t≤20时、 40≤t≤80 、 100≤t≤120， v逐渐减少；
(4)根据图象，填写下表：
2.如图，正三角形ABC内接于圆O，设圆的半径为r。你能写出图中阴影部分的面积S与半径r的函数关系吗？你认为用哪种方法表示他们之前的函数关系比较方便？