2022-2023学年北京市朝阳区高二（下）期末数学试卷(含详细答案解析)

这是一份2022-2023学年北京市朝阳区高二（下）期末数学试卷(含详细答案解析)，共15页。试卷主要包含了单选题，填空题，解答题等内容，欢迎下载使用。

1.已知集合A={−1,0,1,2}，集合B={x|−1≤x<1}，则A∩B=( )
A. {0,1}B. {−1,1}C. {−1,0}D. {−1,0,1}
2.已知α∈(π2,π)，且sin(π−α)=13，则csα=( )
A. −2 23B. −23C. 23D. 2 23
3.已知不等式x2+ax+4<0的解集为空集，则实数a的取值范围是( )
A. (−∞,−4)∪(4,+∞)B. (−∞,−4]∪[4,+∞)
C. (−4,4)D. [−4,4]
4.从集合{2,3,4,5,6,7,8}中任取两个不同的数，则取出的两个数中恰有一个是奇数的概率为( )
A. 27B. 37C. 47D. 67
5.已知a=lg13，b=30.1，c=sin3，则( )
A. a>b>cB. b>c>aC. b>a>cD. c>b>a
6.设a，b∈R，则“(a−b)a2<0”是“aA. 充分而不必要条件B. 必要而不充分条件
C. 充要条件D. 既不充分也不必要条件
7.某学校4名同学到3个小区参加垃圾分类宣传活动，每名同学只能去1个小区，且每个小区至少安排1名同学，则不同的安排方法种数为( )
A. 6B. 12C. 24D. 36
8.已知函数f(x)=sin(2x−π3)，则下列结论正确的是( )
A. 函数f(x+π)的一个周期为π2
B. 函数f(x+π)的一个零点为π6
C. y=f(x)的图象可由y=sin2x的图象向右平移π3个单位长度得到
D. y=f(x)的图象关于直线x=3π2对称
9.某工厂将产生的废气经过过滤后排放，已知过滤过程中的污染物的残留数量P(单位：毫克/升)与过滤时间t(单位：小时)之间的函数关系为P=P0⋅e−kt(t≥0)，其中k为常数，k>0，P0为原污染物数量.该工厂某次过滤废气时，若前4个小时废气中的污染物恰好被过滤掉90%，那么再继续过滤2小时，废气中污染物的残留量约为原污染物的( )
A. 1%B. 2%C. 3%D. 5%.
10.已知定义在R上的函数f(x)满足：
①f(2+x)+f(−x)=0；
②f(−1+x)=f(−1−x)；
③当x∈[−1,1]时，f(x)=csπ2x,x∈[−1,0],1−x,x∈(0,1],
则函数g(x)=f(x)+12在区间[−5,3]上的零点个数为( )
A. 3B. 4C. 5D. 6
二、填空题：本题共6小题，每小题5分，共30分。
11.二项式(x+2x)6的展开式中的常数项是______.(用数字作答)
12.某中学高一、高二、高三年级的学生人数分别为1200，1000，800，为迎接运动会的到来，按照各年级人数所占比例进行分层抽样，选出30名志愿者，则高二年级应选出的人数为______.
13.当x>−1时，函数y=x+4x+1−2的最小值为______，此时x=______.
14.已知a>0，则关于x的不等式x2−4ax−5a2<0的解集是______.
15.若函数y=cs2x的图象在区间(−π4,m)上恰有两个极值点，则满足条件的实数m的一个取值为______.
16.已知集合M为非空数集，且同时满足下列条件：
(ⅰ)2∈M；
(ⅱ)对任意的x∈M，任意的y∈M，都有x−y∈M；
(ⅲ)对任意的x∈M且x≠0，都有1x∈M.
给出下列四个结论：
①0∈M；
②1∉M；
③对任意的x，y∈M，都有x+y∈M；
④对任意的x，y∈M，都有xy∈M.
其中所有正确结论的序号是______.
三、解答题：本题共5小题，共70分。解答应写出文字说明，证明过程或演算步骤。
17.(本小题13分)
设函数f(x)=2sinωxcsωx+m(ω>0,m∈R)，从条件①、条件②、条件③这三个条件中选择两个作为已知，使函数f(x)唯一确定.
(Ⅰ)求ω和m的值；
(Ⅱ)设函数g(x)=f(x−π6)，求g(x)在区间[0,π2]上的最大值.
条件①：f(0)=1；
条件②：f(x)的最小值为0；
条件③：f(x)的图象的相邻两条对称轴之间的距离为π2.
18.(本小题14分)
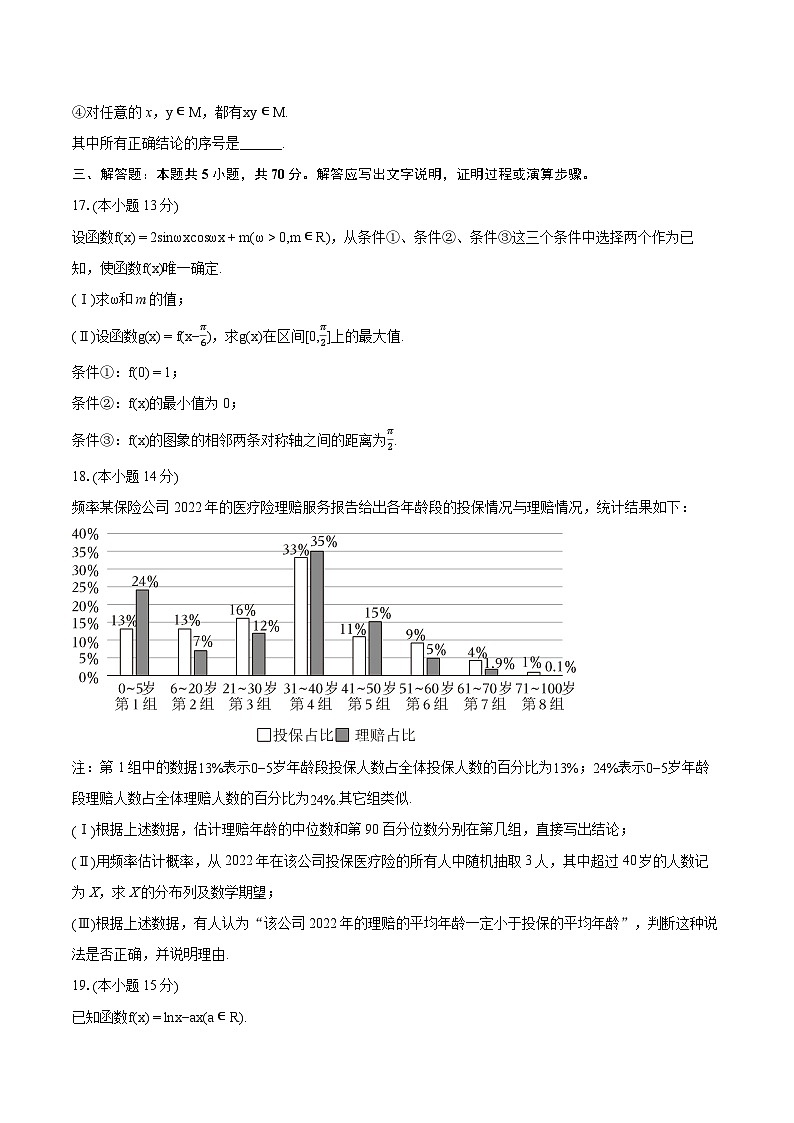
频率某保险公司2022年的医疗险理赔服务报告给出各年龄段的投保情况与理赔情况，统计结果如下：
注：第1组中的数据13%表示0−5岁年龄段投保人数占全体投保人数的百分比为13%；24%表示0−5岁年龄段理赔人数占全体理赔人数的百分比为24%.其它组类似.
(Ⅰ)根据上述数据，估计理赔年龄的中位数和第90百分位数分别在第几组，直接写出结论；
(Ⅱ)用频率估计概率，从2022年在该公司投保医疗险的所有人中随机抽取3人，其中超过40岁的人数记为X，求X的分布列及数学期望；
(Ⅲ)根据上述数据，有人认为“该公司2022年的理赔的平均年龄一定小于投保的平均年龄”，判断这种说法是否正确，并说明理由.
19.(本小题15分)
已知函数f(x)=lnx−ax(a∈R).
(Ⅰ)当a=3时，求曲线y=f(x)在点(1,f(1))处的切线方程；
(Ⅱ)若x=2是f(x)的一个极值点，求f(x)的单调递增区间；
(Ⅲ)是否存在a，使得f(x)在区间(0,e]上的最大值为−2？若存在，求出a的值；若不存在，说明理由.
20.(本小题13分)
已知函数f(x)=e2x，g(x)=m(2x+1)(m∈R).
(Ⅰ)当m=1时，证明f(x)≥g(x)；
(Ⅱ)若直线y=g(x)是曲线y=f(x)的切线，设h(x)=f(x)−g(x)，求证：对任意的a>b，都有h(a)−h(b)a−b<2e2a−2.
21.(本小题15分)
若有穷整数数列A：a1，a2，⋯，an满足1≤ai≤n(i=1,2,⋯,n)，且各项均不相同，则称A为Pn数列.对Pn数列A：a1，a2，⋯，an，设λ1=0，λi=j=1i−1ai−aj|ai−aj|(i=2,3,⋯,n)，则称数列λ(A)：λ1，λ2，⋯，λn为数列A的导出数列.
(Ⅰ)分别写出P4数列2，1，4，3与3，1，4，2的导出数列；
(Ⅱ)是否存在P6数列A使得其导出数列λ(A)的各项之和为0？若存在，求出所有符合要求的P6数列；若不存在，说明理由；
(Ⅲ)设Pn数列A：a1，a2，⋯，an与A′：a′1，a′2，⋯，a′n的导出数列分别为λ(A)：λ1，λ2，⋯，λn与λ(A′)：λ′1，λ′2，⋯，λ′n，求证：ai=a′i(i=1,2,⋯,n)的充分必要条件是λi=λ′i(i=1,2,⋯,n).
答案和解析
1.【答案】C
【解析】解：∵集合A={−1,0,1,2}，集合B={x|−1≤x<1}，
∴A∩B={−1,0}.
故选：C.
直接根据集合的交集运算即可得到答案．
本题主要考查了集合的交集运算，属于基础题．
2.【答案】A
【解析】解：∵sin(π−α)=13，∴sinα=13，
∵α∈(π2,π)，∴csα=− 1−(13)2=−2 23.
故选：A.
由已知和诱导公式求出sinα，再由同角三角函数的关系求出csα.
本题考查三角函数求值，考查同角三角函数的关系和诱导公式的应用，属于基础题．
3.【答案】D
【解析】解：根据题意，不等式x2+ax+4<0的解集为空集，
则有Δ=a2−16≤0，解可得−4≤a≤4，即a的取值范围为[−4,4].
故选：D.
根据题意，由二次函数的性质可得Δ=a2−16≤0，解可得答案．
本题考查一元二次不等式的解法，注意结合二次函数的性质分析，属于基础题．
4.【答案】C
【解析】解：从集合{2,3,4,5,6,7,8}中任取两个不同的数有C72=21种方法，
其中取出的两个数中恰有一个是奇数的有C31C41=12种方法，
∴取出的两个数中恰有一个是奇数的概率为P=1221=47.
故选：C.
先求出任取两个不同的数的方法数，再求出两个数中恰有一个是奇数的方法数，再利用古典概型的概率公式能求出取出的两个数中恰有一个是奇数的概率．
本题考查古典概型的概率公式等基础知识，考查运算求解能力，是基础题．
5.【答案】B
【解析】解：∵a=lg1330=1，0∴b>c>a.
故选：B.
由对数函数的性质，指数函数的性质，正弦函数的有界限可得a，b，c的范围，从而可得出a，b，c的大小关系．
本题考查了对数函数和指数函数的单调性，考查了计算能力，属于基础题．
6.【答案】A
【解析】【分析】
本题考查了不等式，充分必要条件的定义，属于容易题．根据充分必要条件定义判断，结合不等式求解．
【解答】
解：∵a，b∈R，(a−b)a2<0，
∴a由a所以，根据充分必要条件的定义可判断得：
a，b∈R，则“(a−b)a2<0”是a故选A.
7.【答案】D
【解析】解：根据题意，分2步进行分析：
①将4人分为3组，有C42=6种分组方法，
②将分好的3组安排到3个小区，有A33=6种情况，
则有6×6=36种安排方法．
故选：D.
根据题意，分2步进行分析：①将4人分为3组，②再将分好的3组安排到3个小区，由分步计数原理计算可得答案．
本题考查排列组合的应用，涉及分步计数原理的应用，属于基础题．
8.【答案】B
【解析】解：f(x)=sin(2x−π3)，f(x+π)=sin[2(x+π)−π3]=sin(2x−π3)，
最小正周期为π，故A错误；
f(x+π)=sin(2x−π3)，将x=π6代入得y=sin0=0，B正确；
C项，f(x)=sin(2x−π3)=sin2(x−π6)，
则f(x)的图象可由y=sin2x的图象向右平移π6个单位长度得到，故C错误；
D项，f(3π2)=sin(3π−π3)=sinπ3= 32，没有取到最值，故D错误．
故选：B.
将f(x+π)表示出来，可判断A，B项；对应y=sinx的性质，判断D项；根据平移变换规律可得C项．
本题考查三角函数的性质，属于基础题．
9.【答案】C
【解析】解：由题意得，当x=4时，P=P0⋅e4k=10%P0，所以ek=0.114，
则当x=6时，P=P0⋅e6k=P0⋅(ek)6=P0⋅0.132=0.1 10P0，
因为3.1< 10<3.2，所以P≈0.03P0，
即再继续过滤2小时，废气中污染物的残留量约为原污染物的3%.
故选：C.
由题意得，当x=4时，P=P0⋅e4k=10%P0，求得k，再将x=6代入即可得出答案．
本题考查函数模型的运用，考查学生的计算能力，属于中档题．
10.【答案】B
【解析】解：由f(2+x)+f(−x)=0可知，f(x)的图象关于点(1,0)对称，
由f(−1+x)=f(−1−x)可知，f(x)的图象关于直线x=−1对称，
又因为当x∈[−1,1]时，f(x)=csπ2x,x∈[−1,0]1−x,x∈(0,1],
所以画出f(x)在区间[−5,3]上的图象，如图所示：
函数g(x)=f(x)+12在区间[−5,3]上的零点个数，即为函数y=f(x)的图象与直线y=−12在区间[−5,3]上的交点个数，
由图象可知，函数y=f(x)的图象与直线y=−12在区间[−5,3]上的交点个数为4个．
故选：B.
由f(2+x)+f(−x)=0可知，f(x)的图象关于点(1,0)对称，由f(−1+x)=f(−1−x)可知，f(x)的图象关于直线x=−1对称，再结合f(x)在[−1,1]上的解析式画出f(x)在区间[−5,3]上的图象，函数g(x)=f(x)+12在区间[−5,3]上的零点个数，即为函数y=f(x)的图象与直线y=−12在区间[−5,3]上的交点个数，数形结合即可求出结果．
本题主要考查了函数的对称性，考查了函数的零点与方程根的关系，同时考查了数形结合的数学思想，属于中档题．
11.【答案】160
【解析】解：因为(x+2x)6的展开式的通项为Tr+1=C6rx6−r⋅(2x)r=C6r⋅2r⋅x6−2r，
令6−2r=0，得r=3，所以展式常数项为C63⋅23=160.
故答案为：160.
将(x+2x)6的展开式的通项表示出来，令x的指数为0即可得．
本题考查二项式定理，属于基础题．
12.【答案】10
【解析】解：根据分层抽样原理知，抽选出30名志愿者时，高二年级应抽选的人数为：
30×10001200+1000+800=10.
故答案为：10.
根据分层抽样原理，求出高二年级应抽选的人数．
本题考查了分层抽样原理应用问题，是基础题．
13.【答案】1 1
【解析】解：当x>−1时，
函数y=x+4x+1−2=(x+1)+4x+1−3
≥2 (x+1)⋅4x+1−3=1，
当且仅当x+1=4x+1即x=1时等号成立，有最小值1.
故答案为：1；1.
根据基本不等式的凑配法即可求出y=x+4x+1−2的最小值．
本题考查基本不等式的解法，属于基础题．
14.【答案】(−a,5a)
【解析】解：不等式x2−4ax−5a2<0，a>0，
因式分解为(x+a)(x−5a)<0，
对应方程的实数根为−a和5a；
因为a>0，所以5a>−a，
所以关于x的不等式x2−ax−5a2<0的解集为：(−a,5a).
故答案为：(−a,5a).
利用因式分解求出对应方程的实数根，再比较两根的大小，从而写出不等式的解集．
本题考查了含有字母系数的不等式的解法与应用问题，是基础题．
15.【答案】π(答案不唯一)
【解析】解：∵函数y=cs2x的图象在区间(−π4,m)上恰有两个极值点，
又2x∈(−π2,2m)，
∴π<2m≤2π，即π2则满足条件的实数m的一个取值为π.
故答案为：π(答案不唯一).
由题意，利用余弦函数的图象和性质，求出m的范围．
本题主要考查余弦函数的图象和性质，属于基础题．
16.【答案】①③④
【解析】[分析]
本题考查元素与集合的关系，实际上涉及到有理数集对加减乘除运算的封闭性，难点是命题④的推导，其关键点由已知推导出x2∈M，然后由代数式运算得出xy∈M.
①利用条件(ⅰ)和(ⅱ)推理可得；
②利用(ⅰ)，(ⅲ)得12∈M，再结合(ⅱ)可判断；
③首先得出−y∈M，然后由条件(ⅱ)可得结论；
④由已知得出2x∈M，得x2∈M，推导1x−1−1x∈M得出x2∈M，从而有x2，y2，(x+y)22，x2+y22∈M，再由条件(ⅱ)可判断．
[解答]
解：①∵2∈M，∴2−2∈M，即0∈M，①正确；
②∵2∈M，∴12∈M，∴2−12=32∈M，32−12=1∈M，②错；
③∵x，y∈M，又0∈M，∴0−y=−y∈M，所以x−(−y)=x+y∈M，③正确；
④x∈M，1x∈M.由③1x+1x=2x∈M，∴x2∈M，
由②知1∈M，∴x−1∈M，∴1x∈M,1x−1∈M，1x−1−1x=1x(x−1)∈M，∴x(x−1)∈M，
由③得x2=x(x−1)+x∈M，
∴当x，y∈M时，x2，y2，(x+y)22，x2+y22∈M，
∴xy=(x+y)22−x2+y22∈M，④正确，
综上，①③④正确．
故答案为：①③④．
17.【答案】解：(Ⅰ)选①③．
因为f(x)=2sinωxcsωx+m=sin2ωx+m，
由f(0)=1，得m=1.
因为f(x)的图象的相邻两条对称轴之间的距离为π2，
所以T2=π2.
所以T=2π|2ω|=π.
因为ω>0，所以ω=1.
选②③．
因为f(x)=2sinωxcsωx+m=sin2ωx+m，
由f(x)的最小值为0，得m=1.
因为f(x)的图象的相邻两条对称轴之间的距离为π2，
所以T2=π2.
所以T=2π|2ω|=π.
因为ω>0，所以ω=1.
选①②不成立，理由如下：
因为f(x)=2sinωxcsωx+m=sin2ωx+m，
由f(0)=1，得m=1.
由f(x)的最小值为0，得m=1.
无法确定ω的值，故f(x)不是唯一确定，故选①②不成立．
(Ⅱ)由(Ⅰ)可知f(x)=sin2x+1.
g(x)=f(x−π6)=sin(2x−π3)+1.
因为x∈[0,π2]，所以2x−π3∈[−π3,2π3].
所以当2x−π3=π2，即x=5π12时，
g(x)在区间[0,π2]上取得最大值g(5π12)=2.
【解析】(Ⅰ)选①③：由f(0)=1及f(x)的图象的相邻两条对称轴之间的距离为π2求得m，ω的值；
选②③：由f(x)的最小值为0及f(x)的图象的相邻两条对称轴之间的距离为π2求得m，ω的值；
(Ⅱ)g(x)=sin(2x−π3)+1，当x∈[0,π2]时求出2x−π3的范围，从而求得g(x)的最大值．
本题主要考查三角函数的图象与性质，考查运算求解能力，属于中档题．
18.【答案】解：(Ⅰ)由图可知，理赔年龄的中位数在第4组，理赔年龄的第90百分位数在第5组．
(Ⅱ)由图可知，从投保医疗险的人中随机抽取1人超过40岁的概率为14，
X的所有可能取值为0，1，2，3，
P(X=0)=C30(14)0(34)3=2764，
P(X=1)=C31(14)1(34)2=2764，
P(X=2)=C32(14)2(34)1=964，
P(X=3)=C33(14)3(34)0=164，
故X的分布列为：
所以E(X)=0×2764+1×2764+2×964+3×164=34.
(Ⅲ)不正确，
比如理赔的年龄比较靠近每一组区间的右端点，
投保的年龄比较接近每一组区间的左端点，
这样估计的结果就是理赔的平均年龄较大．
用区间的右端点估计理赔的平均年龄为5×0.24+20×0.07+30×0.12+40×0.35+50×0.15+60×0.05+70×0.019+100×0.00=32.13，
用区间的左端点估计投保的平均年龄为0×0.13+6×0.13+21×0.16+31×0.33+41×0.11+51×0.09+61×0.04+71×0.01=26.62，
因为32.13>26.62，所以说法不正确．
【解析】(Ⅰ)根据中位数和百分位数的概念，即可得出结论；
(Ⅱ)求得X的可能取值及对应概率，完成分布列，根据期望公式求解即可；
(Ⅲ)求得该公司2022年的理赔的平均年龄和投保的平均年龄，比较即可得出结论．
本题考查离散型随机变量的分布列和期望，是中档题．
19.【答案】解：(Ⅰ)已知f(x)=lnx−ax，定义域为(0,+∞)，
可得f′(x)=1x−a，
当a=3时，f(x)=lnx−3x，
可得f′(x)=1x−3，
所以f′(1)=−2，
又f(1)=−3，
所以曲线y=f(x)在点(1,f(1))处的切线方程为y+3=−2(x−1)，
即2x+y+1=0；
(Ⅱ)若x=2是f(x)的一个极值点，
所以f′(2)=12−a=0，
解得a=12，
此时f′(x)=1x−12，
当00，f(x)单调递增；
当x>2时，f′(x)<0，f(x)单调递减，
所以当x=2时，函数f(x)取得极大值，满足条件，
则f(x)的单调递增区间为(0,2)；
(Ⅲ)假设存在a，使得f(x)在区间(0,e]上的最大值为−2，
当a≤1e时，
因为x∈(0,e],
所以f′(x)=1x−a≥1e−a≥0，
则f(x)在区间(0,e]上单调递增，
此时f(x)max=f(e)=lne−ae=1−ae，
若1−ae=−2，
解得a=3e，不满足条件；
当a>1e，即0<1a当00，f(x)单调递增；
当1a此时f(x)max=f(1a)=ln1a−1，
若ln1a−1=−2，
解得a=e，满足条件，
综上，当a=e时，f(x)在区间(0,e]上的最大值为−2.
【解析】(Ⅰ)由题意，将a=3代入函数f(x)解析式中，对f(x)进行求导，得到f′(1)，f(1)，代入切线方程中即可求解；
(Ⅱ)若x=2是f(x)的一个极值点，可得f′(2)=0，列出等式求出a的值，再将a代入函数解析式中，利用导数的几何意义即可得到函数f(x)的单调性；
(Ⅲ)假设存在a，使得f(x)在区间(0,e]上的最大值为−2，对a≤1e和a>1e这两种情况进行分析，利用导数的几何意义得到函数f(x)的单调性和最值，再进行检验，进而可得满足条件的a的值．
本题考查利用导数研究函数的单调性和极值，考查了逻辑推理、转化思想、分类讨论和运算能力．
20.【答案】证明：(Ⅰ)当m=1时，设φ(x)=f(x)−g(x)=e2x−2x−1，
则φ′(x)=2e2x−2，令φ′(x)=2e2x−2>0，解得x>0，令φ′(x)=2e2x−2<0，解得x<0，
故φ(x)在区间(−∞,0)上单调递减，在区间(0,+∞)上单调递增；
故φ(x)≥φ(0)=0，故f(x)≥g(x)成立．
(Ⅱ)由已知得f′(x)=2e2x，设切点为P(x0,e2x0)，
则2e2x0=2m且m(2x0+1)=e2x0，解得：x0=0，m=1，
所以g(x)=2x+1，h(x)=e2x−2x−1，
要证h(a)−h(b)a−b<2e2a−2，
即证e2a−2a−e2b+2ba−b<2e2a−2，
即证e2a−e2ba−b<2e2a，即证1−e2b−2a<2(a−b)，
令2a−2b=t，t>0，原不等式等价于1−e−t1，
设F(t)=t+e−t，则F′(t)=1−e−t>0，
所以F(t)在区间(0,+∞)上单调递增，
所以F(t)>F(0)=1，所以t+e−t>1成立，
所以对任意a>b，都有h(a)−h(b)a−b<2e2a−2.
【解析】(Ⅰ)代入m的值，设φ(x)=f(x)−g(x)，求出函数的导数，根据函数的单调性求出函数的单调区间，从而证明结论成立；
(Ⅱ)设切点为P(x0,e2x0)，求出m的值，从而求出h(x)的解析式，问题转化为证1−e2b−2a<2(a−b)，令2a−2b=t，t>0，原不等式等价于1−e−t1，
设F(t)=t+e−t，求出函数的导数，结合函数的单调性证明即可．
本题考查了函数的单调性，最值问题，考查导数的应用以及切线方程问题，考查不等式的证明以及转化思想，是难题．
21.【答案】解：(Ⅰ)2，1，4，3的导出数列为0，−1，2，1，
3，1，4，2的导出数列为0，−1，2，−1；
(Ⅱ)不存在，理由如下：
设A：a1，a2，a3，a4，a5，a6，
则λ1=0，λ2=a2−a1|a2−a1|，λ3=a3−a1|a3−a1|+a3−a2|a3−a2|，λ4=a4−a1|a4−a1|+a4−a2|a4−a2|+a4−a3|a4−a3|，λ5=a5−a1|a5−a1|+a5−a2|a5−a2|+a5−a3|a5−a3|+a5−a4|a5−a4|，λ6=a6−a1|a6−a1|+a6−a2|a6−a2|+a6−a3|a6−a3|+a6−a4|a6−a4|+a6−a5|a6−a5|，
∵ai−aj|ai−aj|∈{−1,1}(i≠j)，
∴λ2∈{−1,1}；λ3∈{−2,0,2}；λ4∈{−3,−1,1,3}；λ5∈{−4,−2,0,2,4}；λ6∈{−5,−3,−1,1,3,5}，
若λ1+λ2+λ3+λ4+λ5+λ6=0，这与λ2，λ4，λ6共三个奇数，λ1+λ2+λ3+λ4+λ5+λ6是奇数相矛盾，
∴λ1+λ2+λ3+λ4+λ5+λ6不可能为0；
证明：(Ⅲ)必要性：
若ai=a′i(i=1,2,⋯,n)，则λ1=λ′1=0，
λi=j=1i−1ai−aj|ai−aj|=j=1i−1a′i−a′j|a′i−a′j|=λ′i(i=2,3,⋯,n)，
充分性：下面用反证法证明，
假设存在i∈{1,2,⋯,n}，使得ai≠a′i，
若an≠a′n，令k=n，
若an=a′n，an−1=a′n−1，⋯，aj+1=a′j+1，aj≠a′j，令k=j，
∵{a1,a2,⋯,an}={a′1,a′2,⋯,a′n}，
∴{a1,a2,⋯,ak}={a′1,a′2,⋯,a′k}，
设a1，a2，⋯，ak−1中有l项比ak小，则有k−l−1项比ak大，
∴λk=l−(k−l−1)=2l−k+1，
设a′1，a′2，⋯，a′k−1中有l′项比a′k小，则有k−l′−1项比a′k大，
∴λ′k=l′−(k−l′−1)=2l′−k+1，
∵{a1,a2,⋯,ak}={a′1,a′2,⋯,a′k}且ak≠a′k，∴l≠l′，
∴λk≠λ′k，矛盾，
∴ai=a′i(i=1,2,⋯,n)，
∴ai=a′i(i=1,2,⋯,n)的充分必要条件是λi=λ′i(i=1,2,⋯,n).
【解析】(Ⅰ)根据导出数列的定义求解；
(Ⅱ)设A：a1，a2，a3，a4，a5，a6，则λ1=0，根据定义分别求出λ2，λ3，λ4，λ5，λ6，再结合ai−aj|ai−aj|∈{−1,1}(i≠j)判断λ2，λ3，λ4，λ5，λ6的奇偶性，从而得到结果；
(Ⅲ)先根据题意证明必要性，再利用反证法证明充分性．
本题主要考查了数列的新定义问题，考查了学生的逻辑推理能力，属于中档题．X
0
1
2
3
P
2764
2764
964
164