统考版2024高考数学二轮专题复习第三篇关键能力为重专题六函数与导数第4讲导数的综合应用课件文

展开

这是一份统考版2024高考数学二轮专题复习第三篇关键能力为重专题六函数与导数第4讲导数的综合应用课件文，共44页。PPT课件主要包含了考点一，考点二，考点三，afxmin，a≤fxmin，所有的，快审题等内容，欢迎下载使用。

考点一　利用导数研究函数的零点
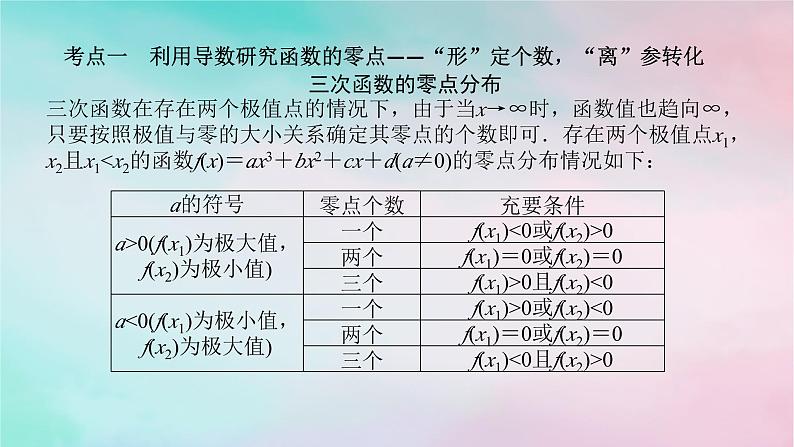
考点一　利用导数研究函数的零点——“形”定个数，“离”参转化三次函数的零点分布三次函数在存在两个极值点的情况下，由于当x→∞时，函数值也趋向∞，只要按照极值与零的大小关系确定其零点的个数即可．存在两个极值点x1，x2且x1由(1)知，h′(x)≤－1，所以h(x)在(0，＋∞)上单调递减．又h(1)＝0，所以当x∈(0，1]时，h(x)≥0；当x∈(1，＋∞)时，h(x)<0.则当x∈(0，1]时，g′(x)≤0；当x∈(1，＋∞)时，g′(x)<0.所以g(x)在(0，＋∞)上单调递减．又当x→0时，g(x)→＋∞，当x→＋∞时，g(x)→0，所以a∈(0，＋∞)．
归纳总结利用导数研究函数零点问题的思路(1)构建函数g(x)(要求g′(x)易求，g′(x)＝0可解)，转化为确定g(x)的零点个数问题求解，利用导数研究该函数的单调性、极值，并确定定义区间端点值的符号(或变化趋势)等，画出g(x)的图象草图，数形结合求解．(2)利用零点存在性定理：先用该定理判断函数在某区间上有零点，然后利用导数研究函数的单调性、极值(最值)及区间端点值符号，进而判断函数在该区间上零点的个数．
对点训练[2020·全国卷Ⅰ]已知函数f(x)＝ex－a(x＋2).(1)当a＝1时，讨论f(x)的单调性；(2)若f(x)有两个零点，求a的取值范围．
考点二　利用导数证明不等式
例 2 [2023·湖北二模]已知函数f(x)＝xex－1，g(x)＝a(ln x＋x)．(1)若不等式f(x)≥g(x)恒成立，求正实数a的值；(2)证明：x2ex>(x＋2)ln x＋2sin x．
所以h(x)min＝a－a ln a－1≥0，设F(a)＝a－a ln a－1(a>0)，因为F′(a)＝1－(1＋ln a)＝－ln a，所以F(a)在(0，1)上单调递增，(1，＋∞)上单调递减，所以F(a)≤F(1)＝0，而依题意必有F(a)≥0，所以F(a)＝0，此时a＝1，所以若不等式f(x)≥g(x)恒成立，则正实数a的值为1.
归纳总结用导数证明不等式的方法(1)利用单调性：若f(x)在[a，b]上是增函数，则①∀x∈[a，b]，则f(a)≤f(x)≤f(b)；②对∀x1，x2∈[a，b]，且x1解析：(1)由题意得y＝xf(x)＝x ln (a－x)，则y′＝ln (a－x)＋x[ln (a－x)]′.因为x＝0是函数y＝xf(x)的极值点，所以y′|x＝0＝ln a＝0，所以a＝1.
考点三　利用导数解决不等式恒(能)成立问题
[f(x)－g(x)]max<0
[f(x)－g(x)]max>0
③对∀x1∈D1，∃x2∈D2，使得f(x1)g(x2)成立，等价于f(x)max>g(x)min.其等价转化思想是：函数f(x)的某一个函数值大于函数g(x)的某一个函数值，即只要有这样的函数值即可，并不要求________函数值．
2．不等式能成立问题的解题关键
[高考5个大题] 解题研诀窍(六) 函数与导数综合问题巧在“转”、难在“分” [思维流程——找突破口]
[技法指导——迁移搭桥]函数与导数问题一般以函数为载体，以导数为工具，重点考查函数的一些性质，如含参函数的单调性、极值或最值的探求与讨论，复杂函数零点的讨论，函数不等式中参数范围的讨论，恒成立和能成立问题的讨论等，是近几年高考试题的命题热点．对于这类综合问题，一般是先转化(变形)，再求导，分解出基本函数，分类讨论研究其性质，再根据题意解决问题．
[典例]　已知函数f(x)＝eln x－ax(a∈R)．(1)讨论f(x)的单调性；(2)a＝e时，证明：xf(x)－ex＋2ex≤0.

相关课件更多