2022-2023学年黑龙江省哈尔滨市香坊区风华中学八年级（下）开学数学试卷（2月份）（五四学制）（含解析）

这是一份2022-2023学年黑龙江省哈尔滨市香坊区风华中学八年级（下）开学数学试卷（2月份）（五四学制）（含解析），共25页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
1.下列图案是轴对称图形的是( )
A. B.
C. D.
2.下列式子中不是分式的是( )
A. 3xB. a2C. x+yxyD. 14mn
3.下列二次根式中是最简二次根式的是( )
A. 7B. 2.5C. 20D. 212
4.下列因式分解错误的是( )
A. x3+xy=x(x2+y)B. 4x2+4x+1=(2x+1)2
C. x2+y2=(x+y)2D. 9x2−y2=(3x+y)(3x−y)
5.下列计算正确的是( )
A. a2⋅a3=a6B. (b3)2=b5C. (ab2)3=a3b6D. c6÷c2=c3
6.已知a+1a=3，则a2+1a2的值是( )
A. 9B. 7C. 5D. 3
7.一辆列车在最近的铁路大提速后，时速提高了20千米/时，则该列车行驶400千米所用的时间比原来少用了30分钟，若该列车提速前的速度是x千米/时，则可列方程为( )
A. 400x−400x−20=30B. 400x−400x+20=0.5
C. 400x+20−400x=0.5D. 400x−20−400x=0.5
8.如图，已知a/​/b，直线l与直线a、b分别交于点A、B，分别以点A、B为圆心，大于12AB的长为半径画弧，两弧相交于点M、N，作直线MN，交直线b于点C，连接AC，若∠ACB=110°，则∠1的度数是( )
A. 55°
B. 50°
C. 40°
D. 35°
9.下列命题中正确的是( )
A. 形如“ a”的式子叫做二次根式
B. 到三角形的三个顶点距离相等的点是三角形三条角平分线的交点
C. 两个数的和与这两个数的差的积等于这两个数的平方差
D. 等腰三角形的高、中线、角平分线互相重合
10.如图，在△ABC中，∠BAC=90°，AC=AB，以AB为边，在△ABC外构造等边△ABD，连接CD，在CD上取一点E，使得∠AEC=45°，DE=2.则下列说法中正确的有个．( )
①∠ACD=15°；②2∠BDC=∠BAC；③EA平分∠BAD；④AE⊥BD；⑤BC=4．
A. 2B. 3C. 4D. 5
二、填空题：本题共10小题，每小题3分，共30分。
11.使代数式 x−1有意义的x的取值范围是 ．
12.将0.000034用科学记数法表示为______．
13.计算： 14÷ 27的结果是______．
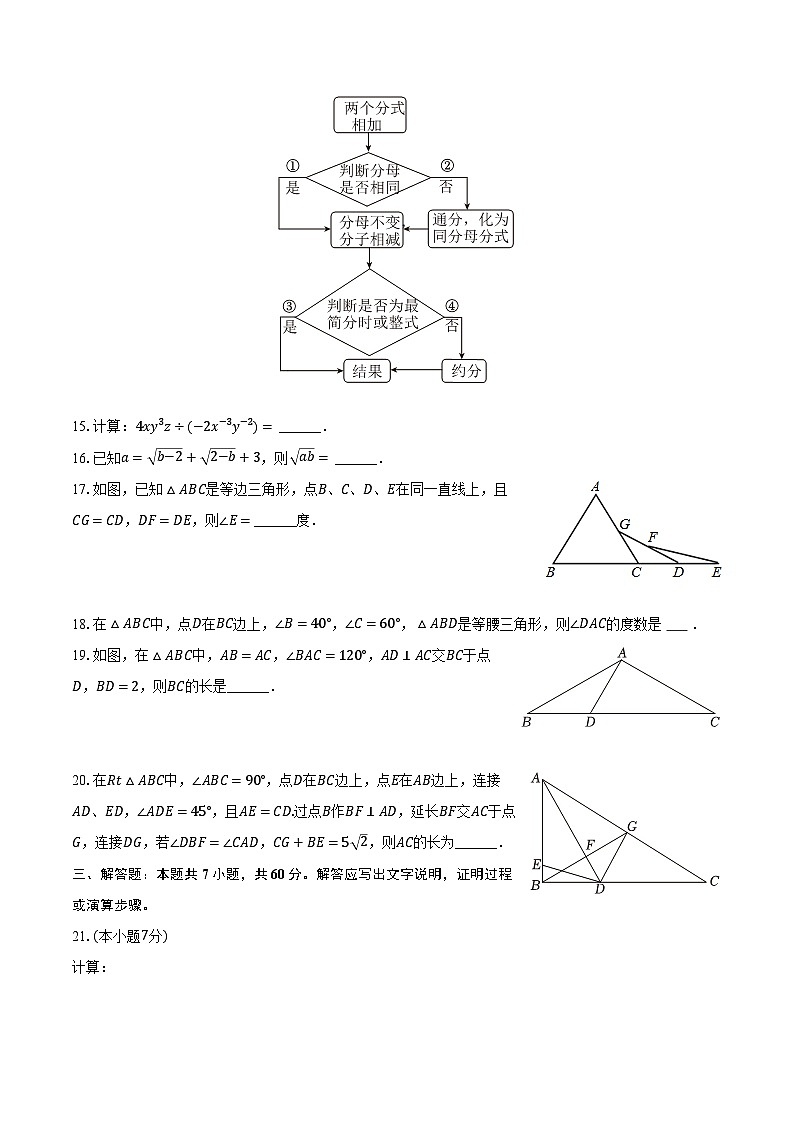
14.学习分式运算过程中，老师布置了一个任务：依据如图的流程图，计算aa+b+2aba2−b2时需要经历的路径是______．
15.计算：4xy3z÷(−2x−3y−2)= ______．
16.已知a= b−2+ 2−b+3，则 ab= ______．
17.如图，已知△ABC是等边三角形，点B、C、D、E在同一直线上，且CG=CD，DF=DE，则∠E=______度．
18.在△ABC中，点D在BC边上，∠B=40°，∠C=60°，△ABD是等腰三角形，则∠DAC的度数是 ．
19.如图，在△ABC中，AB=AC，∠BAC=120°，AD⊥AC交BC于点D，BD=2，则BC的长是______．
20.在Rt△ABC中，∠ABC=90°，点D在BC边上，点E在AB边上，连接AD、ED，∠ADE=45°，且AE=CD.过点B作BF⊥AD，延长BF交AC于点G，连接DG，若∠DBF=∠CAD，CG+BE=5 2，则AC的长为______．
三、解答题：本题共7小题，共60分。解答应写出文字说明，证明过程或演算步骤。
21.(本小题7分)
计算：
(1)(x+1)(x−3)；
(2)计算： 6÷ 13×( 12+ 50)．
22.(本小题7分)
先化简，再求值：xx2−1÷(1−1x+1)，其中x= 2+1．
23.(本小题8分)
如图，在平面直角坐标系中，已知△ABC的三个顶点坐标分别是A(0,2)，B(3,1)，C(1,4)．
(1)画出△ABC关于y轴对称的△AB1C1，并写出点B1的坐标；
(2)在x轴上找出一点E使AE+BE的和最小，写出点E的坐标，并画出确定痕迹；
(3)连接B1E、BE，直接写出四边形B1ABE的面积．
24.(本小题8分)
在①AD=AE，②∠ABE=∠ACD，③FB=FC这三个条件中选择其中一个，补充在下面的问题中，并完成问题的解答．
问题：如图，在△ABC中，∠ABC=∠ACB，点D在AB边上(不与点A，点B重合)，点E在AC边上(不与点A，点C重合)，连接BE，CD，BE与CD相交于点F.若______，求证：BE=CD．
注：如果选择多个条件分别作答，按第一个解答计分．
25.(本小题10分)
某超市准备购进足球和篮球进行销售.每个足球的进价比每个篮球的进价少10元，且用800元购买足球的数量与用1000元购买篮球的数量相同．
(1)求每个足球和篮球的进价分别是多少元；
(2)已知该超市本次购进足球的数量比篮球的数量的2倍少5个，每个足球的销售价是75元，每个篮球的销售价是80元，由于足球的销售量不好，足球售出10个后超市决定将剩余的足球按八折出售，最终将本次购进的足球和篮球全部售出，若使销售的总利润不低于1450元，超市至少购进篮球多少个？
26.(本小题10分)
已知：△ABC中，AB=AC，点D为AC上一点，连接BD并延长至点E，连接AE、CE，使∠BEC=∠BAC．

(1)如图1，当∠BAC=60°时，求证：AE+CE=BE；
(2)如图2，当∠BAC=90°时，(1)中结论是否成立？若成立，请给予证明；若不成立，请直接写出结论：______；
(3)如图3，在(2)的条件下，在BE上截取BF=CE，连接CF，点G在EF上，连接AG，且∠EAG=75°，∠BAG=∠ACF，CF=4 3，求AG的长．
27.(本小题10分)
已知，在平面直角坐标系中，点A(0,m)在x轴的正半轴上，点B(n,m)在第一象限，且a、b满足等式m2−12m+36+ n−6=0，连接AB、OB．

(1)如图1，求m，n的值；
(2)如图2，点C在x轴负半轴上一点，且其横坐标为t，过点C作CD⊥AC，CD=AC，连接AD、OD.设△OCD的面积为S，求S与t之间的关系式(不需要写出t的取值范围)；
(3)如图3，在(2)的条件下，作AE⊥BD，垂足为点E，连接CE交OB于点F，连接DF，交x轴于点G，当DF/​/y轴时，求△ODF的面积．
答案和解析
1.【答案】B
【解析】解：A、不是轴对称，不符合题意；
B、是轴对称图形，符合题意；
C、不是轴对称，不符合题意；
D、不是轴对称，不符合题意；
故选：B．
根据轴对称图形的概念即可求解．在平面内，一个图形沿一条直线折叠，直线两旁的部分能够完全重合的图形为轴对称图形．
本题考查了轴对称图形，能找准对称轴是本题的关键．
2.【答案】B
【解析】解：选项A、C、D的分母中都含有未知数，故它们都是分式；a2是整式．所以不是分式的是B．
故选：B．
根据分式的定义，逐个判断得结论．
本题考查了分式的定义．分式需同时满足三个条件：(1)AB的形式；(2)分子、分母都是整式；(3)分母中含有字母．
3.【答案】A
【解析】解：A、 7是最简二次根式，符合题意；
B、 2.5= 52= 102，不是最简二次根式，不合题意；
C、 20=2 5，不是最简二次根式，不合题意；
D、 212= 102，不是最简二次根式，不合题意．
故选：A．
直接利用最简二次根式的定义分析得出答案即可．
本题主要考查了最简二次根式，正确把握定义：(1)被开方数不含分母；(2)被开方数中不含能开得尽方的因数或因式是解题关键．
4.【答案】C
【解析】解：A、x3+xy=x(x2+y)，因式分解正确，故不符合题意；
B、4x2+4x+1=(2x+1)2，因式分解正确，故不符合题意；
C、x2+y2不能进行因式分解，因式分解不正确，故符合题意；
D、9x2−y2=(3x+y)(3x−y)，因式分解正确，故不符合题意；
故选：C．
根据提公因式法、公式法进行因式分解，逐项判断即可．
本题考查了因式分解；熟练掌握提公因式法和公式法正确进行因式分解是解题的关键．
5.【答案】C
【解析】解：A、a2⋅a3=a5，原式计算错误，故本选项错误；
B、(b3)2=b6，原式计算错误，故本选项错误；
C、(ab2)3=a3b6，计算正确，故本选项正确；
D、c6÷c2=c4，原式计算错误，故本选项错误；
故选：C．
结合选项分别进行同底数幂的乘法和除法、幂的乘方，积的乘方等运算，然后选择正确选项．
本题考查了同底数幂的乘法和除法、幂的乘方，积的乘方等运算，解答本题的关键是掌握各知识点的运算法则．
6.【答案】B
【解析】解：∵a+1a=3，
∴(a+1a)2=9，
∴a2+2+1a2=9，
∴a2+1a2=7，
故选：B．
将题目中的式子完全平方再展开，然后变形即可得到所求式子的结果，本题得以解决．
本题考查完全平方式，解题的关键是明确题意，找出所求问题需要的条件，利用完全平方式解答．
7.【答案】B
【解析】解：∵该列车提速前的速度是x千米/时，
∴提速后的速度是(x+20)千米/时．
∵该列车行驶400千米所用的时间比原来少用了30分钟，
∴可列方程为400x−400x+20=0.5．
故选：B．
由题意可得出提速后的速度是(x+20)千米/时，进而由该列车行驶400千米所用的时间比原来少用了30分钟，即可列出关于x的分式方程．
本题考查分式方程的实际应用．读懂题意，找出等量关系，列出等式是解题关键．
8.【答案】D
【解析】解：∵a/​/b，∠ACB=110°，
∴∠CAD=180°−110°=70°，
根据作图可知，MN垂直平分线段AB，
∴AC=BC，
∴∠ABC=∠BAC，
∵a/​/b，
∴∠ABC=∠1，
∴∠1=∠CAB，
∵∠1+∠CAB=∠CAD=70°，
∴∠1=12×70°=35°，故D正确．
故选：D．
根据a/​/b，∠ACB=110°，得出∠CAD=180°−110°=70°，根据垂直平分线的性质得出AC=BC，根据等腰三角形的性质，得出∠ABC=∠BAC，根据平行线的性质，得出∠ABC=∠1，从而得出∠1=∠CAB，即可求出∠1=12×70°=35°．
本题主要考查了平行线的性质，垂直平分线的性质，等腰三角形的性质，解题的关键是熟练掌握平行线的性质，两直线平行，内错角相等；两直线平行，同旁内角互补．
9.【答案】C
【解析】解：A、形如“ a(a≥0)”的式子叫做二次根式，故不符合题意；
B、到三角形的三个顶点距离相等的点是三角形三条垂直平分线的交点，故不符合题意；
C、两个数的和与这两个数的差的积等于这两个数的平方差，故符合题意；
D、等腰三角形底边上的高、底边上的中线、顶角的角平分线互相重合，故不符合题意；
故选：C．
根据二次根式的定义、三角形的外心、平方差、等腰三角形的性质判断求解即可．
本题考查命题与定理，解题的关键是掌握教材上相关的概念和定理．
10.【答案】D
【解析】解：①∵△ABD为等边三角形，
∴AB=AD=BD，∠ABD=∠ADB=∠BAD=60°，
∵AC=AB，∠BAC=90°，
∴AD=AC，∠DAC=60°+90°=150°，
∴∠ADC=∠ACD=12(180°−150°)=15°，故①正确；
②∵∠BDC=∠BDA−∠ADC=60°−15°=45°，∠BAC=90°，
∴2∠BDC=∠BAC，故②正确；
③∵∠AEC=45°，∠ADC=15°，
∴∠DAE=∠AEC−∠ADC=45°−15°=30°，
∵∠BAD=60°，
∴∠BAE=∠BAD−∠DAE=30°，
∴∠DAE=∠BAE，
∴EA平分∠BAD，故③正确；
④延长AE交BD于点F，如图所示：
∵△ABD是等边三角形，AE平分∠BAD，
∴AE⊥BD，故④正确；
⑤∵∠DFE=90°，∠DEF=∠AEC=45°，
∴∠EDF=90°−45°=45°，
∴∠EDF=∠DEF，
∴DF=EF，
∵DF2+EF2=DE2，
∴2DF2=22，
解得：DF= 2或DF=− 2(舍去)，
∵△ABD是等边三角形，AE平分∠BAD，
∴BD=2DF=2 2，
∴AB=AC=2 2，
∴BC= AB2+AC2=4，故⑤正确；
综上分析可知，正确的有5个，故D正确．
故选：D．
①根据等边三角形的性质和等腰直角三角形的性质，得出∠ACD=15°，可以判定①；
②求出∠BDC=45°，即可得出②正确；
③求出∠DAE=∠BAE，即可得出③正确；
④根据等边三角形的性质，即可得出④正确；
⑤根据勾股定理求出BC=4，即可得出⑤正确．
本题主要考查了等边三角形的性质，勾股定理，等腰三角形的判定和性质，解题的关键是熟练掌握等边三角形和等腰三角形的性质．
11.【答案】x≥1
【解析】【分析】
根据二次根式有意义的条件：被开方数为非负数求解即可．
【解答】
解：因为代数式 x−1有意义，
所以x−1≥0，
解得：x≥1．
故答案为：x≥1．
【点评】
本题考查了二次根式有意义的条件，掌握被开方数为非负数是解题关键．
12.【答案】3.4×10−5
【解析】解：0.000034=3.4×10−5，
故答案为：3.4×10−5．
科学记数法的形式是：a×10n，其中1≤|a|