

2023-2024学年江苏省泰州市泰兴市七年级(上)期末数学试卷(含解析)
展开这是一份2023-2024学年江苏省泰州市泰兴市七年级(上)期末数学试卷(含解析),共18页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
1.−2的倒数是( )
A. −2B. −12C. 12D. 2
2.下列各组数中,互为相反数的是( )
A. −(+2)和+(−2)B. −(−3)2和−9C. −(−3)和−(+3)D. −(+6)和−|−6|
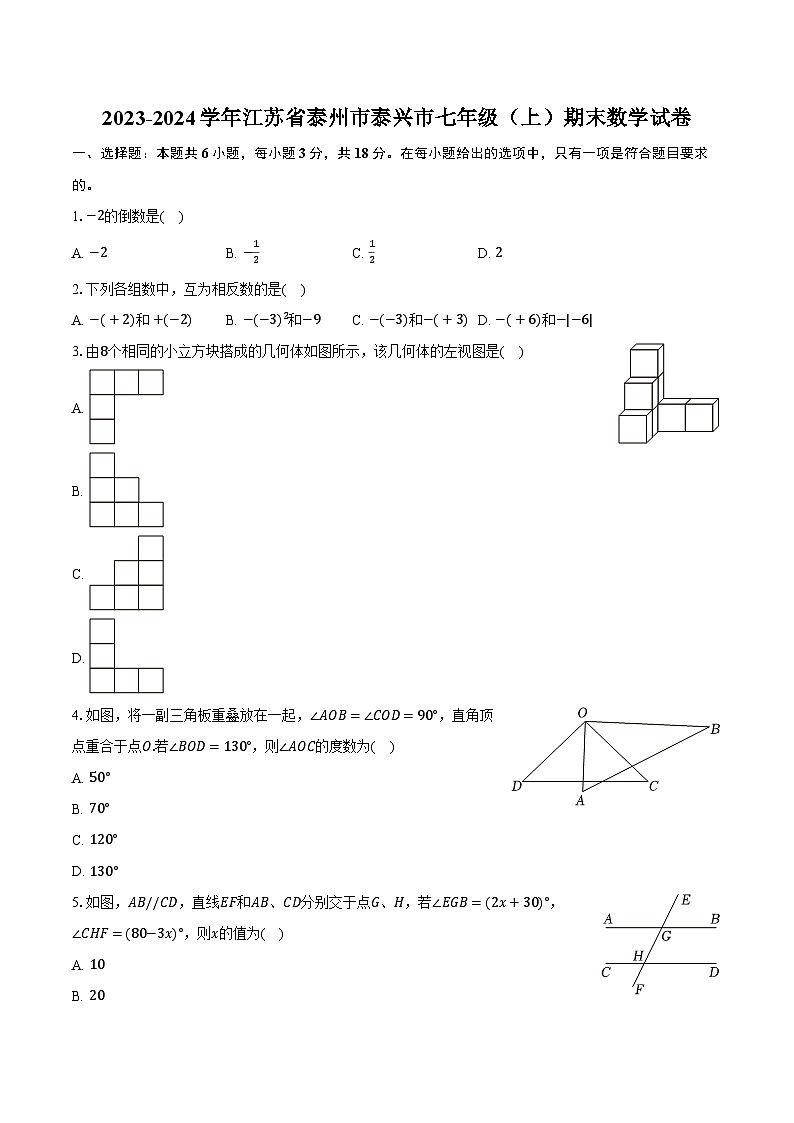
3.由8个相同的小立方块搭成的几何体如图所示,该几何体的左视图是( )
A.
B.
C.
D.
4.如图,将一副三角板重叠放在一起,∠AOB=∠COD=90°,直角顶点重合于点O.若∠BOD=130°,则∠AOC的度数为( )
A. 50°
B. 70°
C. 120°
D. 130°
5.如图,AB//CD,直线EF和AB、CD分别交于点G、H,若∠EGB=(2x+30)°,∠CHF=(80−3x)°,则x的值为( )
A. 10
B. 20
C. 100
D. 110
6.已知a为常数,且无论k取何值,关于x的方程ak−2x=kx−4的解总是x=2,则a的值为( )
A. −1B. 1C. −2D. 2
二、填空题:本题共10小题,每小题3分,共30分。
7.一个数的平方等于81,则这个数是______.
8.地球与月球的平均距离为384000km,将384000这个数用科学记数法表示为________.
9.若一个棱柱有12个顶点,则这个棱柱有______个面.
10.已知∠A=44°35′,则∠A的余角的度数为______.
11.已知关于x的方程ax+3=5的解为x=4,则a的值为______.
12.元旦节前夕,班主任为学生们准备了若干块糖果,若每人分4块,则多32块,若每人分5块,则还差8块.设班级有x人,根据题意列方程得______.
13.如果a=b,那么称a与b互为“平等数”,若4m2−2n与n+2互为“平等数”,则代数式8m2−6n+2024= ______.
14.已知摄氏温度(℃)与华氏温度(T)之间的转换关系是:tC=59(tF−32)或tF=95tC+32(tC表示t摄氏度,tF表示t华氏度).某天同一时刻A地的气温是86T,B地气温是25℃,则这一时刻气温较高的是______地(填“A”或“B”).
15.已知,如图,点C在线段AB上,且AB=16cm,BC=4cm,点M、N分别是AB、BC的中点,则线段MN的长度为______cm.
16.如图,分别过直线AB上的点C和点D作射线CF、DE,∠BCF=60°,∠EDB=90°,射线DG从DE开始绕着点D以6度/秒的速度顺时针旋转,射线CH从CF开始绕着点C以1度/秒的速度顺时针旋转,在射线DG旋转一周的过程中,经过______秒,射线DG、射线CH所在的直线互相垂直.
三、解答题:本题共10小题,共102分。解答应写出文字说明,证明过程或演算步骤。
17.(本小题10分)
计算:
(1)(−49)+(−59)−(−9);
(2)(56−12−712)+(−124).
18.(本小题10分)
解方程:
(1)3(2x−1)−2(2−3x)=41;
(2)x−42=3x+57−2.
19.(本小题8分)
先化简,再求值:(2xy2−3x2y)−2(3x2y+xy2−1),其中x=2,y=14.
20.(本小题8分)
如图,点C、A、F在一条直线上,AD⊥BC于点D,FE⊥BC于点E,交AB于点G,若AD平分∠BAC,则∠F与∠5相等吗?为什么?请把下面的解题过程补充完整并在括号内填写依据.
解:相等.
∵AD⊥BC于点D,FE⊥BC于点E,
∴∠1=∠2=90°.
∴ ______// ______(同位角相等,两直线平行),
∴∠4=∠5(______),
∠3=∠F(______).
∵AD平分∠BAC,
∴ ______=∠ ______.
∴∠F=∠5.
21.(本小题10分)
如图,直线AB、CD相交于点O,OE平分∠AOC,若∠EOD=146°,求∠DOB的度数.
22.(本小题10分)
利用网格仅用无刻度直尺按照要求完成作图并回答问题.
(1)过点A作射线OB的垂线,垂足为点C;
(2)过点A作射线OA的垂线,交射线OB于点D;
(3)比较AC和OD的大小,并说明理由.
23.(本小题10分)
折纸是进一步理解直线平行的条件和平行线的性质,发展推理能力的一种有效的方法.
(1)如图1,四边形ABCD是长方形纸片,AB//CD,折叠纸片,折痕为EF,AE和CD交于点G.探究∠A′EF和∠CFE的数量关系,并说明理由;
(2)如图2,在(1)中折叠的基础上,再将纸片折叠,使得C′G经过点E,折痕为GH.探究两次折痕EF和GH的位置关系,并说明理由.
24.(本小题10分)
某校七年级组织数学知识竞赛,共设20道选择题,各题分值相同,每题必答.下表记录了3个参赛者的得分情况.
(1)观察表格数据并填空,参赛者答对1道题得______分,答错1道题得______分;
(2)参赛者D得80分,他答对了几道题?
(3)参赛者E说他得了68分,你认为可能吗?为什么?
25.(本小题12分)
如图是某长方体包装盒的展开图,具体数据如图所示,且长方体盒子的长是高的2倍.
(1)展开图的6个面分别标有如图所示的序号,则原包装盒与①相对的面是______(填序号);
(2)若设长方体的高为x cm,则:
①长方体的宽为______cm(用含x的式子表示);
②求长方体包装盒的体积.
26.(本小题14分)
已知点A、B、C、D在数轴上,点A和点C表示的数分别为−8、2,点B在点A的右侧,点D在点C的右侧,且AB=4,CD=2.
(1)直接写出点B和点D表示的数分别为:______、______;
(2)若线段AB沿着数轴向右以2个单位长度/秒的速度运动,同时线段CD沿着数轴向左以1个单位长度/秒的速度运动,设运动的时间为t(秒),t>0.
①若B和D重合,则t的值为______,若A和C重合,则t的值为______;
②若线段AB和线段CD重叠部分为1个单位长度,求运动时间t的值;
③当83
1.【答案】B
【解析】【分析】
根据倒数的定义:乘积是1的两个数互为倒数.
本题主要考查倒数的定义,解决本题的关键是熟记乘积是1的两个数互为倒数.
【解答】
解:因为−2×(−12)=1.
所以−2的倒数是−12,
故选:B.
2.【答案】C
【解析】解:A、−(+2)=−2,+(−2)=−2,所以−(+2)和+(−2)相等,故此选项不符合题意;
B、−(−3)2=−9,所以−(−3)2和−9相等,故此选项不符合题意;
C、−(−3)=3,−(+3)=−3,所以−(−3)和−(+3)互为相反数,故此选项符合题意;
D、−(+6)=−6,−|−6|=−6,所以−(+6)和−|−6|相等,故此选项不符合题意;
故选:C.
根据相反数、绝对值、有理数的乘方计算,然后得出答案即可.
本题考查了相反数、绝对值、有理数的乘方,熟练掌握这些知识点是解题的关键.
3.【答案】B
【解析】解:这个几何体的左视图为:.
故选:B.
根据左视图的定义判断即可.
本题考查简单组合体的三视图,解题的关键是理解三视图的定义.
4.【答案】A
【解析】解:∵∠AOB=∠COD=90°,
∴∠AOC+∠BOC=90°,
即∠BOC=90°−∠AOC,
∵∠BOD=130°,
∴∠COD+∠BOC=90°+90°−∠AOC=130°,
∴∠AOC=50°,
故选:A.
由∠AOB=90°得出∠AOC+∠BOC=90°,由∠BOD=130°得出∠COD+∠BOC=130°,从而求出∠AOC的度数.
本题考查了余角和补角,熟练掌握余角的性质是解题的关键.
5.【答案】A
【解析】解:∵AB//CD,
∴∠EGB=∠EHD,
∵∠EHD=∠CHF,
∴∠EGB=∠CHF,
∵∠EGB=(2x+30)°,∠CHF=(80−3x)°,
∴2x+30=80−3x,
解得x=10,
故选:A.
根据平行线的性质和对顶角的性质,可以得到∠EGB和∠CHF的关系,然后即可求得x的值.
本题考查平行线的性质、对顶角的性质,解答本题的关键是明确题意,利用数形结合的思想解答.
6.【答案】D
【解析】解:把x=2代入方程ak−2x=kx−4,得ak−4=2k−4,
ak−2k=−4+4,
(a−2)k=0,
∵a为常数,且无论k取何值,关于x的方程ak−2x=kx−4的解总是x=2,
∴a−2=0,
∴a=2.
故选:D.
把x=2代入方程ak−2x=kx−4得出ak−4=2k−4,求出(a−2)k=0,根据方程的解总是x=2得出a−2=0,再求出a即可.
本题考查了一元一次方程的解,能得出关于a的方程a−2=0是解此题的关键.
7.【答案】±9
【解析】解:92=81,(−9)2=81,
所以平方等于81的数是±9.
则这个数是±9.
根据平方的定义.
平方是正数的数有两个且互为相反数.
8.【答案】3.84×105
【解析】【分析】
此题考查科学记数法的表示方法.科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数,表示时关键要正确确定a的值以及n的值.科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值>1时,n是正数;当原数的绝对值<1时,n是负数.
【解答】解:将384000这个数用科学记数法表示为3.84×105,
故答案为:3.84×105.
9.【答案】8
【解析】解:因为棱柱有12个顶点,
所以这个棱柱是六棱柱,
所以六棱柱有8个面,
故答案为:8.
根据棱柱的顶点数、面数、棱数之间的关系得出答案.
本题考查认识立体图形,掌握棱柱的特征是正确判断的前提.
10.【答案】45°25′
【解析】解:∵∠A=44°35′,
∴∠A的余角的度数=90°−∠A=89°60′−44°35′=45°25′,
故答案为:45°25′.
根据余角的定义,以及度分秒的进制进行计算,即可解答.
本题考查了余角和补角,度分秒的换算,准确熟练地进行计算是解题的关键.
11.【答案】12
【解析】解:把x=4代入方程ax+3=5,得4a+3=5,
4a=5−3,
4a=2,
a=12.
故答案为:12.
把x=4代入方程ax+3=5得出4a+3=5,再根据等式的性质求出方程的解即可.
本题考查了一元一次方程的解,能得出关于a的方程4a+3=5是解此题的关键.
12.【答案】4x+32=5x−8
【解析】解:根据题意,得4x+32=5x−8.
故答案为:4x+32=5x−8.
根据糖果的数量相同列一元一次方程即可.
本题考查了由实际问题抽象出一元一次方程,解题的关键是找出题目中的相等关系,有的题目所含的等量关系比较隐藏,要注意仔细审题,耐心寻找.
13.【答案】2028
【解析】解:∵4m2−2n与n+2互为“平等数”,
∴4m2−2n=n+2,
∴n=4m2−23,
∴8m2−6n+2024
=8m2−6×4m2−23+2024
=8m2−2(4m2−2)+2024
=2028,
故答案为:2028.
根据4m2−2n=n+2,将n用关于m的代数式表示出来,并代入8m2−6n+2024计算求值即可.
本题考查代数式求值,将一个字母用含另一个字母的代数式表示出来是本题的关键.
14.【答案】A
【解析】解:令tF=86,
则tC=59×(86−32)=59×54=30(°C),
∵30>25,
∴这一时刻气温较高的是A地,
故答案为:A.
令tF=86,代入tC=59(tF−32)中即可求出A地的摄氏温度,与B地的摄氏温度比较即可.
本题考查了代数式求值,有理数的大小比较,求出A地的摄氏温度是解题的关键.
15.【答案】6
【解析】解:∵点M、N分别是AB、BC的中点,
∴AM=BM=12AB=8cm,BN=CN=12BC=2cm,
∴MN=BM−BN=8−2=6(cm).
故答案为:6.
根据线段中点的定义以及图形中线段的和差关系进行计算即可.
本题考查两点间的距离,掌握线段中点的定义以及图形中线段的和差关系是正确解答的关键.
16.【答案】12或48
【解析】解:(1)如图:
∴∠GDB=∠EDB−∠EDG=90°−6t°,
∴∠CDP=∠GDB=90°−6t°,
又∠CPD=∠DCF+∠FCH=60°+t°,
∠CPD=90°,
∴(90−6t)°+(60+t)°=90°,
t=12(秒).
如图:
∴∠GDE=360°−6t°,
∴∠ADG=90°−∠GDE=90°−(360−6t)°=6t°−270°.
又∠HCB=∠HCF+∠FCB=60°+t°,
∴60°+t°=90°+(6t°−270°),
∴t=48(秒).
故答案为:12或48.
情况一:如图:∠GDB=∠EDB−∠EDG=90°−6t°,∠CDP=∠GDB=90°−6t°,又∠CPD=∠DCF+∠FCH=60°+t°,列式为(90−6t)°+(60+t)°=90°,故t=12(秒).
情况二:如图:∠GDE=360°−6t°,∠ADG=90°−∠GDE=90°−(360−6t)°=6t°−270°,列式为60°+t°=90°+(6t°−270°),故t=48(秒).
本题考查了一元一次方程的运用,在旋转中把角度表示出来是解题关键.
17.【答案】解:(1)(−49)+(−59)−(−9)
=−49+(−59)+9
=−1+9
=8;
(2)(56−12−712)+(−124)
=(1012−612−712)+(−124)
=−14+(−124)
=−724.
【解析】(1)根据有理数的加减运算法则计算即可;
(2)先算括号里面的,然后根据有理数的加法法则计算即可.
本题考查了有理数的加减运算,熟练掌握有理数的加减运算法则是解题的关键.
18.【答案】解:(1)3(2x−1)−2(2−3x)=41,
6x−3−4+6x=41,
6x+6x=41+3+4,
12x=48,
x=4;
(2)x−42=3x+57−2,
7(x−4)=2(3x+5)−28,
7x−28=6x+10−28,
7x−6x=10−28+28,
x=10.
【解析】(1)按照解一元一次方程的步骤:去括号,移项,合并同类项,系数化为1进行计算,即可解答;
(2)按照解一元一次方程的步骤:去分母,去括号,移项,合并同类项,系数化为1进行计算,即可解答.
本题考查了解一元一次方程,熟练掌握解一元一次方程的步骤是解题的关键.
19.【答案】解:原式=2xy2−3x2y−6x2y−2xy2+2
=2xy2−2xy2−3x2y−6x2y+2
=−9x2y+2,
当x=2,y=14时,
原式=−9×22×14+2
=−9×4×14+2
=−9+2
=−7.
【解析】先根据去括号法则和合并同类项法则进行化简,然后把x,y的值代入化简后的式子进行计算即可.
本题主要考查了整式的化简求值,解题关键是熟练掌握去括号法则和合并同类项法则.
20.【答案】AD EF 两直线平行,内错角相等 两直线平行,同位角相等 ∠3 4
【解析】解:相等.理由如下:
∵AD⊥BC于点D,FE⊥BC于点E,
∴∠1=∠2=90°,
∴AD//EF(同位角相等,两直线平行),
∴∠4=∠5(两直线平行,内错角相等),
∠3=∠F(两直线平行,同位角相等),
∵AD平分∠BAC,
∴∠3=∠4,
∴∠F=∠5,
故答案为:AD,EF;两直线平行,内错角相等;两直线平行,同位角相等;∠3,4.
先证AD//EF,则∠4=∠5,∠3=∠F,再由角平分线定义得∠3=∠4,即可得出结论.
本题考查了平行线的判定与性质以及角平分线定义,熟练掌握平行线的判定与性质是解题的关键.
21.【答案】解:∵∠EOD=146°,
∴∠EOC=180°−146°=34°,
∵OE平分∠AOC,
∴∠DOB=∠AOC=2∠EOC=68°.
【解析】根据平角的定义,角平分线的定义以及对顶角相等进行计算即可.
本题考查对顶角、邻补角,角平分线,掌握角平分线的性质以及对顶角、邻补角的定义是正确解答的前提.
22.【答案】解:(1)如图,直线AC即为所求;
(2)如图,直线AD即为所求;
(3)∵AC=3,OD=6,
∴AC
【解析】(1)根据要求画出图形;
(20根据要求画出图形;
(3)根据AC,OD的长度判断即可.
本题考查作图−应用与设计作图,垂线等知识,解题的关键是掌握网格特征,正确作出图形.
23.【答案】解:(1)结论:∠A′EF=∠CFE.
理由:∵AB//CD,
∴∠CFE=∠AEF,
由翻折变换的性质可知∠AEF=∠A′EF,
∴∠A′EF=∠CFE;
(2)结论:EF//GH.
理由:∵AB//CD,
∴∠AEG=∠CGE,
由翻折变换的性质可知∠FEG=12∠AEG,∠HGE=12∠CGE,
∴∠FEG=∠HGE,
∴EF//GH.
【解析】(1)结论:∠A′EF=∠CFE.利用平行线的性质翻折变换的性质证明;
(2)结论:EF//GH,证明∠FEG=∠HGE即可.
本题考查翻折变换,平行线的性质,解题的关键是理解题意,掌握翻折变换的性质.
24.【答案】6 −2
【解析】解:(1)由A参赛者知:对一题得120÷20=6(分),
由B参赛者知:112−19×6=−2(分),
故答案为:答对1道题得6分,答错1道题得−2分;
(2)设参赛者D答对了x道题,
∴6x−2(20−x)=80,
∴x=15.
故答案为:答对了15道题.
(3)设参赛者E答对了m道题,
∴6m−2(20−m)=68,
∴m=272,
∵m为整数,
故答案为:不可能.
(1)由A参赛者得对一题的得分,由B参赛者得错一题的得分;
(2)设参赛者D答对了x道题,列出方程6x−2(20−x)=80,然后进行计算;
(3)设参赛者E答对了m道题,列出方程6m−2(20−m)=68,得到结果不为整数即可判断.
本题考查了一元一次方程的应用,根据题意列出等式是解题关键.
25.【答案】⑥ 35−4x2或20−x2
【解析】解:(1)根据长方体表面展开图的“相间、Z端是对面”可知,面①与面⑤是对面,
故答案为:⑥;
(2)①设长方体的高为x cm,长方体盒子的长是高的2倍.
所以长方体的长为2x cm,
所以长方体的宽为35−4x2cm或20−x2cm,
故答案为:35−4x2或20−x2;
②长方形的长为2x cm,高为xcm,则长方体的宽为:35−4x2或20−x2 cm,由题意得,
35−4x2=20−x2,
解得x=5,
即长方体的长为10cm,宽为152cm,
∴长方体的体积为10×5×152=375(cm3),
答:这个长方体的纸盒的体积为375cm3.
(1)根据长方体表面展开图的“相间、Z端是对面”进行判断即可;
(2)根据展开图中长、宽、高的关系列方程求出长、宽、高,再由体积的计算方法进行计算即可.
本题考查正方体相对两个面上的文字,一元一次方程,掌握正方体表面展开图的特征,列出一元一次方程是正确解答的关键.
26.【答案】−4 4 83 103 ①
【解析】解:(1)点A表示的数为−8,点B在点A的右侧,且AB=4,
∴点B表示的数为−8+4=−4,
∵点C表示的数为2,点D在点C的右侧,CD=2,
∴点D表示的数为2+2=4,
故答案为:−4,4.
(2)①若B和D重合,则(2+1)t=4−(−4),
∴t=83;
若A和C重合,则(2+1)t=2−(−8),
∴t=103;
故答案为:83,103.
②当B点超过C点1个单位长度时,此时,线段AB和线段CD重叠部分为1个单位长度,
∴(2+1)t=2−(−4)+1,
∴t=73;
当A点超过C点3个单位长度时,此时,线段AB和线段CD重叠部分为1个单位长度,
∴(2+1)t=4−(−8)+1,
∴t=133;
故答案为:t=73分钟或133分钟;
③答:①BC+AD是定值,定值是6.
解:当t=83和103时,点B表示的数为−4+2×83=43和−4+2×103=83,
故当83
故当83
当t=83和103时,点A表示的数为−8+2×83=−83和−8+2×103=−43,
故当83
故当83
∴BC+AD=−6+4t+12−4t=6,
故答案为:①,6.
(1)点A表示的数为−8,且AB=4,得到点B表示的数;点C表示的数为2,CD=2,得到点D表示的数.
(2)①由B和D重合,得(2+1)t=4−(−4),可求t,由A和C重合,得(2+1)t=2−(−8),可求t.
②当B点超过C点1个单位长度时,可得(2+1)t=2−(−4)+1,可求t,当A点超过C点3个单位长度时,可得(2+1)t=4−(−8)+1,可求t.
③根据t=83和103时,求出点B和点C表示的数的范围,同理求出点A和点D表示的数的范围,再判断定值即可.
本题考查了数轴的知识,根据题意列出方程是解题关键.参赛者
答对题数
答错题数
得分
A
20
0
120
B
19
1
112
C
18
2
104
相关试卷
这是一份2022-2023学年江苏省泰州市泰兴市九年级(上)期末数学试卷(含详细答案解析),共23页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
这是一份2023-2024学年江苏省泰州市泰兴市七年级(上)期中数学试卷(含解析),共20页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
这是一份2023-2024学年江苏省泰州市泰兴市八年级(上)期中数学试卷(含解析),共27页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。












