浙江省2024年初中学业水平评价适应性考试数学试卷

这是一份浙江省2024年初中学业水平评价适应性考试数学试卷，共6页。试卷主要包含了 计算2024的结果是， 在浙江，环境保护早已深入人心， 《孙子算经》中有一道题等内容，欢迎下载使用。

（试卷满分120分 考试时间120分钟）
一．选择题：本大题有10小题，每小题3分，共30分．请选出每小题中一个最符合题意的选
项，不选、多选、错选，均不给分．
1． 作为中国东南沿海地区的重要省份，浙江省拥有丰富的人口资源和经济发展活力．2024年1月，浙江省统计局发布数据：2023年浙江省生产总值约为82500亿元，总量迈上了新台阶．数据82500亿用科学计数法表示为（ ）
A. 8.25×1011 B. 8.25×1012 C. 8.25×1013 D. 82.5×1011
2． 计算(－1)2024的结果是（ ）
A. 1 B. －1 C. 2024 D. －2024
3． 在浙江，环境保护早已深入人心．为了倡导这一价值理念，某中学举行“五水共治”知识
竞赛，共有四组题目．两位同学一起参赛，抽中同一组题目的概率为（ ）
A. B. C. D.
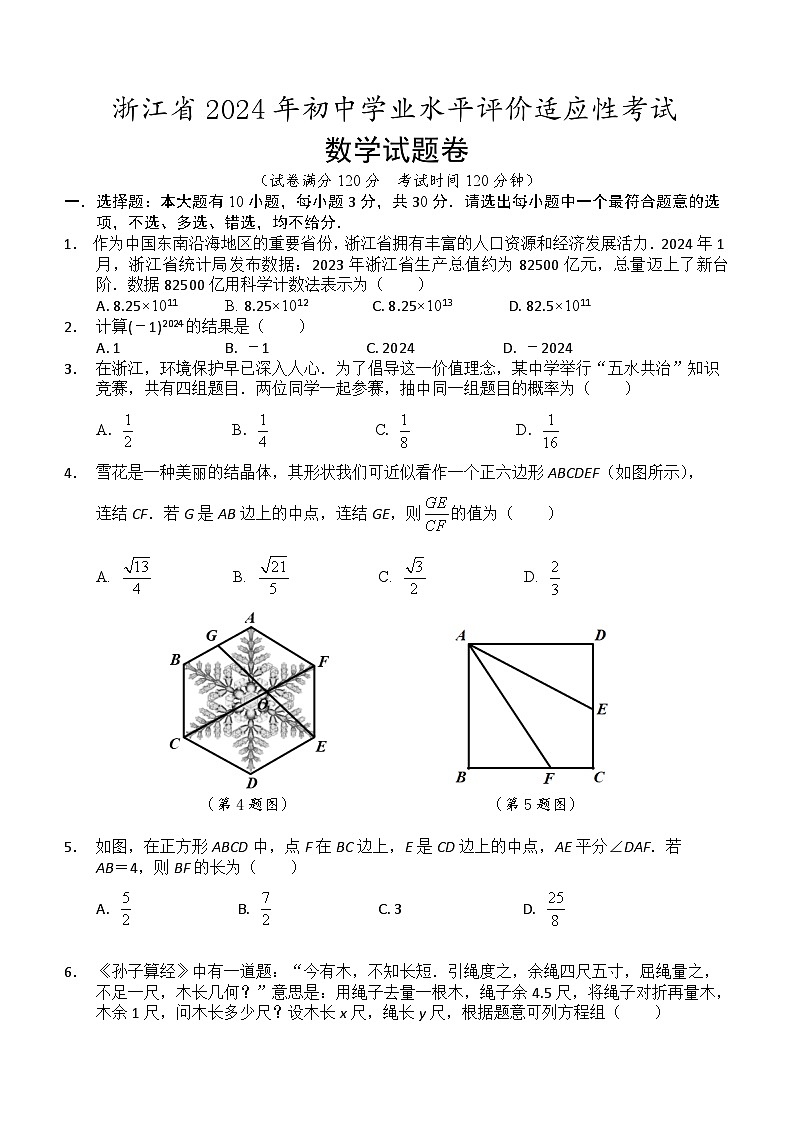
4． 雪花是一种美丽的结晶体，其形状我们可近似看作一个正六边形ABCDEF（如图所示），
连结CF．若G是AB边上的中点，连结GE，则的值为（ ）
A. B. C. D.

（第4题图） （第5题图）
5． 如图，在正方形ABCD中，点F在BC边上，E是CD边上的中点，AE平分∠DAF．若
AB＝4，则BF的长为（ ）
A. B. C. 3 D.
6． 《孙子算经》中有一道题：“今有木，不知长短．引绳度之，余绳四尺五寸，屈绳量之，
不足一尺，木长几何？”意思是：用绳子去量一根木，绳子余4.5尺，将绳子对折再量木，木余1尺，问木长多少尺？设木长x尺，绳长y尺，根据题意可列方程组（ ）
A. B. C. D.
7． 小江在某数学读物上看到了如下问题：“在△ABC中，AB＝3，AC＝5，BC＝6，求BC边上的中线长．”你可能不会求解，但你可以根据所学知识，帮助小江推断下面答案可能的一项是（ ）
A. B. 2 C. D. 3
8． 如图，在四边形ABCD中，AB＝AD＝3，BD⊥CD．记∠CBD＝α，∠BAD＝β．若4α＝β，
tanα＝，则BC的长为（ ）
A. B. C. D.

（第8题图） （第9题图）
9． 如图，在菱形ABCD中，∠ABC＝60°，AB＝8，连结对角线AC、BD交于点O．M是BD
的三等分点，N是OC的中点，则MN的长为（ ）
A. B. C. D.
10．有5个外观完全相同的小球，其中一个质量不合格，但不知是偏轻还是偏重．若要用天平找出这个小球，则至少应称量的次数为（天平平衡即为称量一次）（ ）
A. 1 B. 2 C. 3 D. 4
二．填空题：本大题有6小题，每小题4分，共24分．
11．已知实数x，y（x＞y）满足x2＋y2＝12，x2y＋xy2＝8，则x－y的值为__________．
12．小江参加了射击比赛，总共7轮，成绩分别为9环、7环、9环、8环、7环、8环、8环，
在这一组数据中，平均数为__________环，众数为__________环．
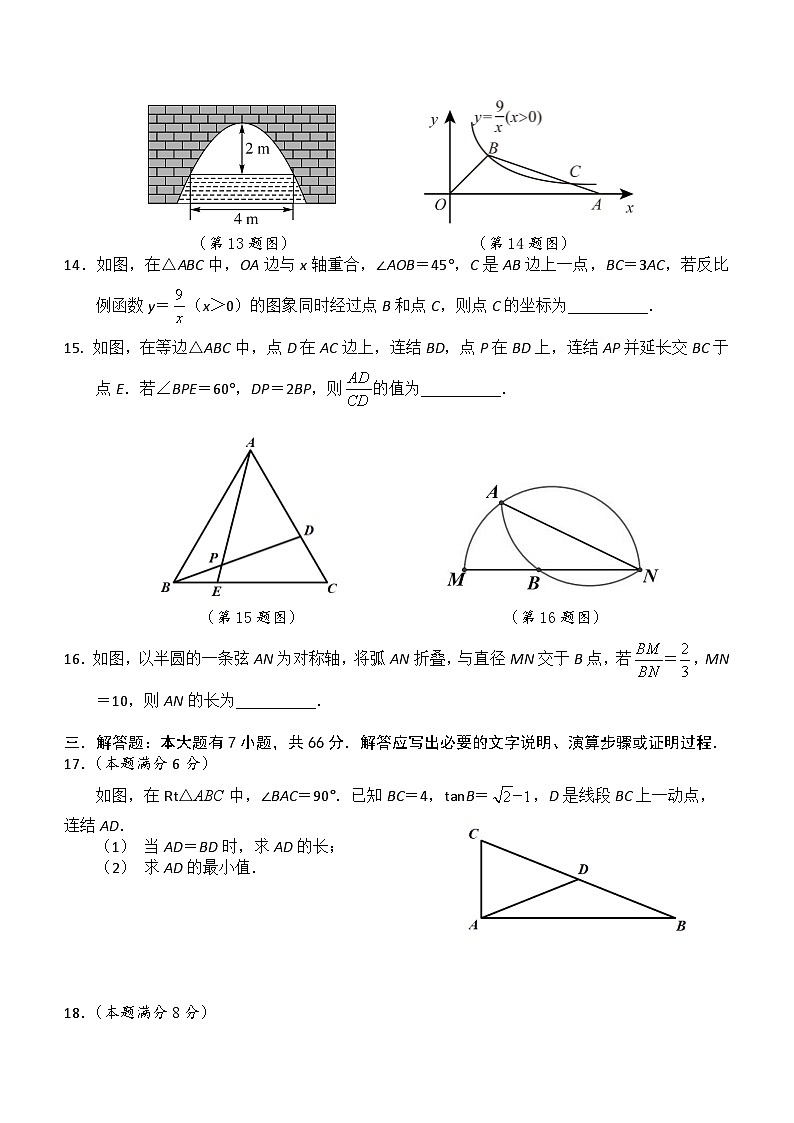
13．如图为一座抛物线形拱桥，当桥顶离水面2 m时，水面宽4 m．若水面下降1 m，则水面的宽度为__________．

（第13题图） （第14题图）
14．如图，在△ABC中，OA边与x轴重合，∠AOB＝45°，C是AB边上一点，BC＝3AC，若反比例函数y＝（x＞0）的图象同时经过点B和点C，则点C的坐标为__________．
15. 如图，在等边△ABC中，点D在AC边上，连结BD，点P在BD上，连结AP并延长交BC于点E．若∠BPE＝60°，DP＝2BP，则的值为__________．

（第15题图） （第16题图）
16．如图，以半圆的一条弦AN为对称轴，将弧AN折叠，与直径MN交于B点，若，MN＝10，则AN的长为__________．
三．解答题：本大题有7小题，共66分．解答应写出必要的文字说明、演算步骤或证明过程．
17．（本题满分6分）
如图，在Rt△ABC中，∠BAC＝90°．已知BC＝4，tanB＝，D是线段BC上一动点，
连结AD．
（1） 当AD＝BD时，求AD的长；
（2） 求AD的最小值．
18．（本题满分8分）
某校正在举行“传承吴越文化，弘扬勾践精神”主题活动，为获悉同学们对于吴越文化的
了解程度，学校随机问卷调查了若干名学生，设置：非常了解、了解、了解很少、不了解四个选项，要求每名学生只选其中一项，并根据调查结果绘制了如下两种不完整的统计图．

（1） 求此次调查的学生人数，并求出图2中“非常了解”对应的扇形圆心角度数；
（2） 若全校共有800名学生，调查结果为“不了解”的学生需要接受文化培训，请你
估计全校总共有多少学生要接受培训？
19．（本题满分8分）
如图，小江一家乘汽车从家出发，前往景区游玩，经2.5小时到达目的地．下面是他们离家的距离y（千米）关于汽车行驶时间x（小时）的函数图象．
（1） 小江家到景区的距离为__________千米；
（2） 出发1.5小时内，汽车行驶的速度为__________千米/时；
（3） 求AB段的解析式；出发2小时后，离景区还有多远？
20．（本题满分10分）
如图，在矩形ABCD中，AB＝3，AD＝4．点M、N分别是AD、CD边上的动点，连结MN，将△DMN沿MN翻折，D的对应点为E．
（1） 当MN与AC重合时，求BE的长；
（2） 当MN＝，|DM－DN|＝2时，问：
①求CE的长；
②求∠MBN的度数．
21．（本题满分10分）
用小立方块搭一个几何体，使它从正面和上面看到的形状如下图所示，从上面看到形状图
中小正方形中的字母表示在该位置上小立方块的个数，请解答下列问题：
（1） a＝__________，b＝__________，c＝__________；
（2） 这个几何体最少由__________个小立方块搭成；
（3） 请在网格图中画出小立方块最多时几何体的左视图．
22．（本题满分12分）
在平面直角坐标系中，二次函数y＝x2＋(a－3)x＋c的图象与y轴的交点为(0，3)．
（1） 求c的值；
（2） 若二次函数的图象经过点(1，2)，求a的值；
（3） 已知点A，B的坐标分别为(1，0)和(2，0)，若二次函数的图象与线段AB恰有一个
交点，直接写出a的取值范围．
23．（本题满分12分）
如图，在半径为5的⊙O中，点C在弦AB上运动，作AC的垂直平分线交AB上方的圆弧
于点D，连结AD、CD．
（1） 若圆心O到弦AB的距离为3，M是AD的中点，求：
①弦AB的长；
②AD的取值范围；
③BM的最小值；
若∠AOB＝90°，CD恰好经过圆心O，求AC的长．

备用图 备用图