（决胜中考）2024年江苏省中考数学常考题模拟卷（一）

这是一份（决胜中考）2024年江苏省中考数学常考题模拟卷（一），共29页。试卷主要包含了请将答案正确填写在答题卡上，窗棂即窗格等内容，欢迎下载使用。

注意事项：
1．答题前填写好自己的姓名、班级、考号等信息
2．请将答案正确填写在答题卡上
一、单选题
1．下列四个选项中，为无理数的是（ ）
A．0B．C．D．﹣3
2．下列运算正确的是（ ）
A．B．
C．D．
3．窗棂即窗格（窗里面的横的、竖的或斜的格）是中国传统木构建筑的框架结构设计，窗棂上雕刻有线槽和各种化纹，构成种类繁多的优美图案，下列表示我国古代窗棂样式结构图案中，既是轴对称图形又是中心对称图形的是（ ）
A．B．C．D．
4．某小组在一次“在线测试”中做对的题数分别是，对于这组数据，下列判断错误的是（ ）
A．众数是B．中位数是C．平均数是D．方差是
5．如图，点D在的边的延长线上，且，若，， 则的度数是（ ）
A．B．C．D．
6．如图，为测楼房BC的高，在距离楼房30米的A处测得楼顶的仰角为α，则楼高BC为（ ）
A．30tanα米B．米C．30sinα米D．米
7．东南环立交是苏州中心城区城市快速内环道路系统的重要节点，也是江苏省最大规模的城市立交．左图是该立交桥的部分道路示意图（道路宽度忽略不计），A为立交桥入口，D、G为出口，其中直行道为、、，且；弯道是以点O为圆心的一段弧，且、、所对的圆心角均为．甲、乙两车由A口同时驶入立交桥，均以的速度行驶，从不同出口驶出，期间两车到点O的距离y（m）与时间x（s）的对应关系如右图所示，结合题目信息，下列说法错误的是（ ）
A．该段立交桥总长为672 mB．从G口出比从D口出多行驶192m
C．甲车在立交桥上共行驶22sD．甲车从G口出，乙车从D口出
8．如图，已知矩形的一边长为12，点P为边上一动点，连接、，且满足，则的值可能是（ ）
A．6B．6.8C．D．
二、填空题
9．春暖花开，科学兴趣小组发现一种花瓣的花粉颗粒的直径约为，将数据0.00065用科学记数法表示为 ．
10．开始进行中考数学一轮复习课前，李浩同学将七（上）、七（下）、八（上）3本数学教科书随机摞放在课桌上，七（上）、七（下）数学教科书相邻的概率是 ．
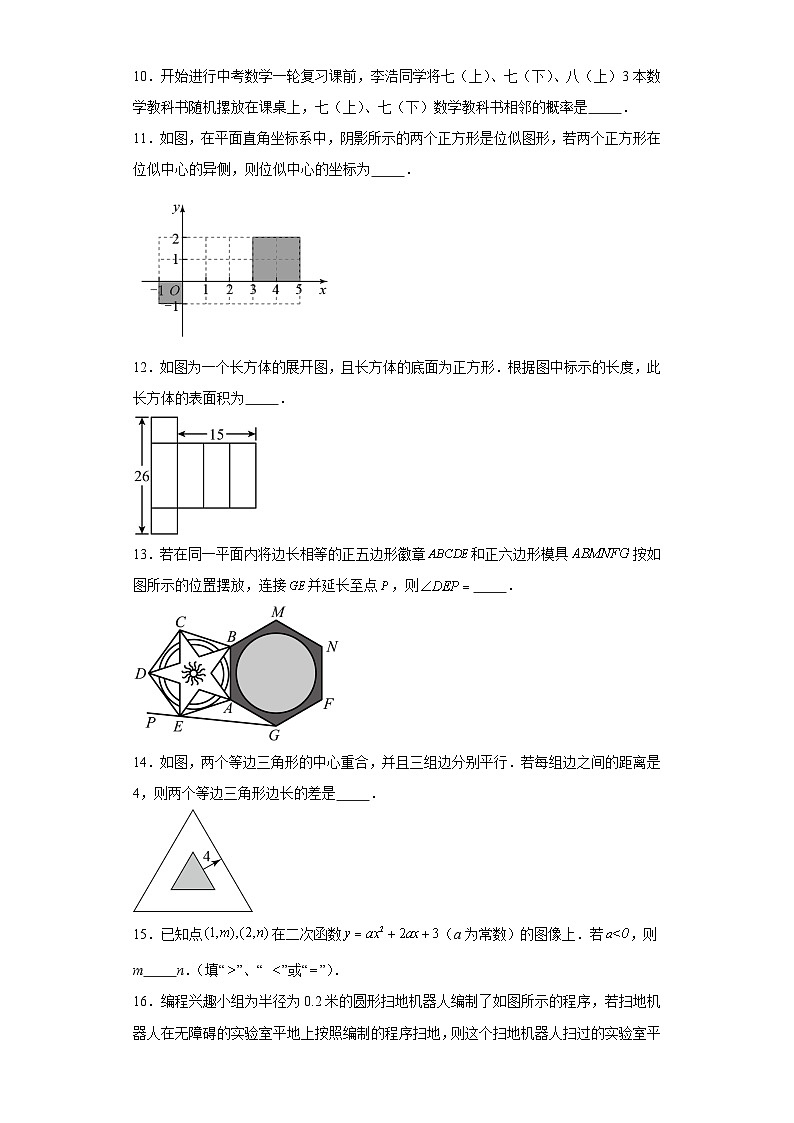
11．如图，在平面直角坐标系中，阴影所示的两个正方形是位似图形，若两个正方形在位似中心的异侧，则位似中心的坐标为 ．
12．如图为一个长方体的展开图，且长方体的底面为正方形．根据图中标示的长度，此长方体的表面积为 ．
13．若在同一平面内将边长相等的正五边形徽章和正六边形模具按如图所示的位置摆放，连接并延长至点，则 ．
14．如图，两个等边三角形的中心重合，并且三组边分别平行．若每组边之间的距离是4，则两个等边三角形边长的差是 ．
15．已知点在二次函数（a为常数）的图像上．若，则m n．（填“”、“ ”或“”）．
16．编程兴趣小组为半径为0.2米的圆形扫地机器人编制了如图所示的程序，若扫地机器人在无障碍的实验室平地上按照编制的程序扫地，则这个扫地机器人扫过的实验室平地的面积是 米．
三、解答题
17．计算：．
18．解不等式组：．
19．先化简、再求值：，其中．
20．已知：如图，在△ABC中，∠ABC、∠ACB的平分线相交于点O，且MN∥BC，分别交AB、AC于点M、N．求证：MN＝BM+CN．
21．“微信运动”被越来越多的人关注和喜爱，某兴趣小组随机抽取部分教师某日微信运动中的步数情况并进行统计整理，将他们的日步行步数（步数单位：万步）进行统计后分为A，B，C，D，E五个等级，并绘制了如图所示不完整的统计图表，请根据信息，解答下列问题：
教师日行走步数频数表
（1）这次抽样调查的样本容量是 ；在扇形统计图中，D组所对应的扇形圆心角度数为 ．
（2）补全频数分布直方图；
（3）若该市约有40000名教师，估计日行走步数超过1.2万步（包含1.2万步）的教师约有多少名？
22．“漏壶”是一种古代计时器，在社会实践活动中，某小组同学根据“漏壶”的原理制作了如图①所示的液体漏壶，漏壶是由一个圆锥和一个圆柱组成的，中间连通，液体可以从圆锥容器中匀速漏到圆柱容器中，实验开始时圆柱容器中已有一部分液体．
【实验观察】（1）下表是实验记录的圆柱体容器液面高度（厘米）与时间（小时）的数据：
在如图②所示的直角坐标系中描出上表的各点，用光滑的线连接；
【探索发现】（2）请你根据表中的数据及图象，用所学过的一次函数、二次函数、反比例函数的知识确定与之间的函数解析式；
【结论应用】（3）如果本次实验记录的开始时间是上午，那么当圆柱体容器液面高度达到12厘米时是几点？
23．如图，在中，，，．点P从点A出发，以的速度沿运动：同时，点Q从点B出发，以的速度沿运动．当点Q到达点C时，P、Q两点同时停止运动．设动点运动的时间为t（s）．
(1)当t为何值时，的面积为；
(2)求四边形面积的最小值．
24．已知：为的直径，O为圆心，点A为圆上一点，过点B作的切线交的延长线于点F，点C为上一点，且，连接交于点E．

(1)如图1，求证：；
(2)如图2，点H为内部一点，连接，．若，的半径为10，，求的长．
25．如图1，抛物线经过， 且与x轴正半轴交于点B，与y轴交于点C，点D是抛物线的顶点，连接，直线l过点B、C．
(1)填空： ； 直线l的函数表达式为： ．
(2)已知直线平行于y轴，交抛物线及x轴于点P、G．当时（如图2），直线与线段分别相交于E、F两点，试证明线段总能组成等腰三角形．
(3)在（2）的条件下，如果此等腰三角形的顶角是的2倍，请求出此时t的值．
26．在边长为8的等边三角形中，为的中点，分别为上任意一点，连接，将线段绕点顺时针旋转得到线段，连接交于点，连接．
(1)如图1，点与点重合，且的延长线过点，证明：四边形是菱形；
(2)如图2，的延长线交于点，当时，求的度数；
(3)如图3，为的中点，连接为直线上一动点，连接，将沿翻折至所在平面内，得到，连接，直接写出线段长度的最小值．
题号
一
二
三
总分
得分
组别
步数（万步）
频数
A
0≤x＜0.4
8
B
0.4≤x＜0.8
15
C
0.8≤x＜1.2
12
D
1.2≤x＜1.6
10
E
x≥1.6
b
时间（小时）
1
2
3
4
5
…
圆柱体容器液面高度（厘米）
6
10
14
18
22
…
参考答案：
1．C
【分析】根据无理数的定义判断即可．
【详解】解：0，，﹣3都是有理数，是无理数，
故选：C．
【点睛】本题考查了无理数，注意带根号的要开不尽方才是无理数，无限不循环小数为无理数．如π，，0.8080080008…（每两个8之间依次多1个0）等形式．
2．A
【分析】根据同底数幂的乘法，合并同类项，积的乘方及完全平方公式的计算法则进行计算，然后做出判断．
【详解】解：A、正确，该选项符合题意；
B、，该选项不符合题意；
C、，该选项不符合题意；
D、，该选项不符合题意；
故选：A．
【点睛】本题考查同底数幂的乘法，合并同类项，积的乘方及完全平方公式的计算，掌握计算法则正确计算是解题关键．
3．D
【分析】根据轴对称图形与中心对称图形的概念求解．
【详解】解：A选项，是轴对称图形，不是中心对称图形，故此选项不符合题意；
B选项，既不是轴对称图形，也不是中心对称图形，故此选项不符合题意；
C选项，是中心对称图形，不是轴对称图形，故此选项不符合题意；
D选项，既是轴对称图形，也是中心对称图形，故此选项符合题意；
故选：D．
【点睛】此题主要考查了中心对称图形与轴对称图形的概念．轴对称图形的关键是寻找对称轴，图形两部分折叠后可重合，中心对称图形是要寻找对称中心，旋转180度后两部分重合．
4．D
【分析】根据平均数，众数，中位数，方差的定义求解判断即可．
【详解】解：把这组数据从小到大排列为，处在最中间的数是8，
∴这组数据的中位数为8，故B不符合题意；
∵这组数据中8出现了3次，出现的次数最多，
∴这组数据的众数为8，故A不符合题意；
这组数据的平均数为，故C不符合题意；
这组数据的方差为 ，故D符合题意；
故选D．
【点睛】本题主要考查了求平均数，众数，中位数，方差，熟知平均数，众数，中位数，方差的定义是解题的关键．
5．B
【分析】根据平行线的性质求出，根据三角形外角性质得出即可．
【详解】解：∵，，
∴，
∵，
∴，
故选：B．
【点睛】此题考查三角形外角性质和平行线的性质，能熟练地运用性质进行推理是解此题的关键．
6．A
【详解】在Rt△ABC中，，∴BC＝AC·tanα，即BC＝30tanα米．
故选A．
7．C
【分析】由两车到点O的距离y（m）与时间x（s）的对应关系图，在段行驶时间是8s，在段行驶时间是（s），通过计算可判断选项A和B；14s后乙车距点O的距离越来越远，甲车距点O的距离暂未改变，可判断选项C和D．
【详解】解：由题意可得（m），
在段行驶时间是（s），（m）
，、、所对的圆心角均为
该段立交桥总长为：（m），A正确；
从G口出比从D口出多行驶：（m），B正确；
14s后乙车距点O的距离越来越远，甲车距点O的距离暂未改变，
甲车从G口出，乙车从D口出，D正确；
甲车在立交桥上行驶时间：（s），C错；
故选：C．
【点睛】本题考查行程问题，解题关键是从到一定点的距离与时间关系图中分析出实际的行程以及所用的时间，根据路程速度时间，计算各段的长度；本题的易错点是y表示车到点O的距离，若y值不变即表示绕圆心O行驶．
8．B
【分析】考虑两个临界值，点P为边上一动点，若点P与点A重合， 最小，时，求得为满足条件的最大值；若点P在中点时， 最大，时，求得为满足条件的最小值．
【详解】解：动点P在中点时， 最大；
取临界值分两种情况：
（1）当动点P与点A重合时， 最小，当时，
，即
解得，
此时是满足题意的最大值；
（2）当动点P在中点时， 最大，当时，
在和中，
在上取一点E，使，
则，
设，则，，
，即
，
此时是满足题意的最小值；
综上所述：，即
选项中，仅B符合要求；
故选：B．
【点睛】本题考查临界值，当临界值取得最小时，对应线段取得最大值，当临界值取得最大时，对应线段取得最小值，特殊角的锐角三角函数需构造等腰三角形，得到含有的直角三角形，求出对应线段．
9．
【分析】根据科学记数法和负整数指数的意义求解．
【详解】解：．
故答案为：．
【点睛】本题考查了科学记数法-表示绝对值较小的数，关键是用为负整数）表示绝对值较小的数．
10．
【分析】利用随机概率的求解方法列树状图求解即可．
【详解】解：记七（上）、七（下）、八（上）3本书分别为A、B、C，利用树状图得到从上至下排列得到摆放情况：
等可能的情况一共有6种，其中七（上）、七（下）即A、B相邻的情况有4种，故七（上）、七（下）数学教科书相邻的概率是,
故答案为：．
【点睛】本题考查随机事件种概率的求解，利用树状图或表格进行概率求解是解题的关键．
11．
【分析】连接各组对应点，它们在两个正方形之间相交于点，则点为位似中心，然后写出点坐标即可．
【详解】解：如图，点为位似中心，．
故答案为：．
【点睛】本题考查位似变换：位似的两个图形不仅是相似图形，而且对应顶点的连线相交于一点，对应边互相平行（或共线），掌握位似变换的性质是解题的关键．
12．
【分析】根据展开图，可以求得原来长方体的底面的边长和高，然后计算长方体的表面积即可．
【详解】解：设原长方体底面边长为，长方体高为，
，，
解得，，
长方体的表面积为：，
故答案为：．
【点睛】本题考查几何体的展开图，解答本题的关键是明确题意，利用数形结合的思想解答．
13．
【分析】根据正边形内角和，则正边形一个内角的度数，即可求得正五边形与正六边形每个内角的度数，由周角是可得的度数，再根据是等腰三角形可求出，最后根据平角是即可求解．
【详解】解：五边形是正五边形，
，
六边形是正六边形，
，
,
正五边形与正六边形的边长相等，
，
是等腰三角形，
，
．
故答案为：．
【点睛】本题考查了正多边形内角和公式，以及求正多边形每个内角的度数，理解并熟练记忆公式，灵活根据题意运用等腰三角形两底角相等、以及平角、周角相结合求角度是解题的关键．
14．
【分析】做辅助线如详解所示，由题意可得，由每组边之间的距离是4可求出和的长，即可求解．
【详解】解：做辅助线如图所示，则，
等边三角形的中心重合，并且三组边分别平行，
，
，
，
，
两个等边三角形边长的差是，
故答案为：．
【点睛】本题考查利用等边三角形的性质和含角的直角三角形求线段的长度，解题的关键是做辅助线构造含角的直角三角形，理解两个等边三角形边长的差即是与的和．
15．
【分析】根据二次函数的性质即可判定．
【详解】解：二次函数的解析式为，
该抛物线对称轴为，
．
当时，随的增大而减小，
，
，
故答案为：．
【点睛】本题主要考查对二次函数图象上点的坐标特征，二次函数的性质等知识点的理解和掌握，能求出对称轴和根据二次函数的性质求出正确答案是解此题的关键．
16．
【分析】简单绘制路线图，围成的几何图形每个外角都是，根据任意多边形外角和都是得出共有六条边，且长度分别为2米和1米交替出现，可得出行走路线总长度，根据半径求出扫过的面积．
【详解】解：如图所示，围成图形的每个外角都是，
扫过的面积是6个长方形面积+6个60°角的扇形面积+6个底角为60°的等腰梯形面积，
扫过的面积= （平方米），
故答案为：．
【点睛】本题主要考查根据每个外角都相等以及任意多边形外角和都是求出几何图形的边数，确定扫过的面积，解题的难点是理解扫过的面积是6个长方形面积+6个60°角的扇形面积+6个梯形面积．
17．
【分析】原式第一项利用绝对值的代数意义化简，第二项利用特殊角的三角函数值计算，第三项利用负指数幂法则计算，最后一项化为最简二次根式，计算即可得到结果．
【详解】原式
．
【点睛】本题考查了实数的运算，二次根式的加减运算，熟练掌握法则是解题关键．
18．
【分析】分别解两个不等式得到和x＜7，然后根据大大小小找不到确定不等式组的解集．
【详解】解不等式，得：，
解不等式，得：x<7，
则不等式组的解集为．
【点睛】本题考查了解一元一次不等式组：解一元一次不等式组时，一般先求出其中各不等式的解集，再求出这些解集的公共部分，利用数轴可以直观地表示不等式组的解集．解集的规律：同大取大；同小取小；大小小大中间找；大大小小找不到．
19．，．
【分析】先根据分式的混合计算法则化简，再根据得到即可得到答案．
【详解】解：
，
∵，
∴，
∴原式．
【点睛】本题主要考查了分式的化简求值，熟知分式的混合计算法则是解题的关键．
20．见解析
【分析】由∠ABC、∠ACB的平分线相交于点O，∠MBO=∠OBC，∠OCN=∠OCB，利用两直线平行，内错角相等，利用等量代换可∠MBO=∠MOB，∠NOC=∠OCN，然后即可证明．
【详解】解：∵∠ABC、∠ACB的平分线相交于点O，
∴∠MBO=∠OBC，∠OCN=∠OCB，
∵MN∥BC，
∴∠OBC=∠MOB，∠NOC=∠OCB，
∴∠MBO=∠MOB，∠NOC=∠OCN，
∴BM=MO，ON=CN，
∴MN=MO+ON，即MN=BM+CN．
【点睛】此题考查学生对等腰三角形的判定与性质和平行线性质的理解与掌握．此题关键是证明△BMO，△CNO是等腰三角形．
21．（1）50；72°；（2）见解析；（3）12000名．
【分析】（1）由B组人数及其所占百分比可得被调查的总人数，用360°乘以D组人数占被调查人数的比例即可得；
（2）根据各组人数之和等于样本容量求出E组人数，从而补全图形；
（3）用总人数乘以样本中D、E组人数和所占比例即可得．
【详解】解：（1）这次调查的样本容量为15÷30%＝50，
在扇形统计图中，D组所对应的扇形圆心角度数为360°×＝72°，
故答案为：50，72°；
（2）E组对应频数为50﹣（8+15+12+10）＝5，
补全频数分布直方图如下：
（3）40000×＝12000，
答：估计日行走步数超过1.2万步（包含1.2万步）的教师约有12000名．
【点睛】本题考查扇形统计图、条形统计图的数据分析、频数、用样本估计总体等知识，是重要考点，难度较易，掌握相关知识是解题关键．
22．（1）见解析；（2）是一次函数，一次函数的解析式为：；（3）圆柱体容器液面高度达到12厘米时对应时间为．
【分析】（1）将各点在坐标系中直接描出即可；
（2）观察发现，时间每增加1小时，圆柱体容器液面高度读数增加，发现它们位于同一直线上，利用待定系数法即可求解；
（3）当时，代入（2）中解析式即可求出时间，再结合实验开始时间为，即可求解．
【详解】解：（1）将表格中各点在直角坐标系中描出来如下图所示：
；
（2）分析表格中数据发现，时间每增加1小时，圆柱体容器液面高度读数增加，观察直角坐标系中点的特点，发现它们位于同一直线上，
设直线解析式为，代入点和点，
得到，解得，
∴直线的解析式为：；
（3）当圆柱体容器液面高度达到12厘米时，即时，代入中，
得，
解得，
∴经过小时后圆柱体容器液面高度达到12厘米，
∵实验记录的开始时间是上午，
∴圆柱体容器液面高度达到12厘米时对应的时间为，即对应时间为．
【点睛】本题考查待定系数法求一次函数的解析式、一次函数的实际应用问题，读懂题目，掌握一次函数的图形及性质是解决本题的关键．
23．(1)或时，的面积为；
(2)四边形面积的最小值为．
【分析】（1）利用两点运动的速度表示出的长，进而表示出的面积；把代入，解方程可得结论；
（2）利用配方法求出函数顶点坐标求得面积的最大值，即得四边形面积的最小值．
【详解】（1）解：由题意得：，，
；
由题意得：，
解得或，
∴或时，的面积为；
（2）解：∵且，
∵，
∴当时，的面积最大，最大值是．
此时，四边形面积取得最小值，最小值为．
【点睛】此题是三角形和二次函数的综合题，主要考查了动点运动问题，三角形的面积，二次函数的应用，难度适中，正确表示出的长是解题关键．
24．(1)见解析
(2)16
【分析】（1）由圆周角定理可得，即，再根据切线的性质可得，再由等腰三角形的性质得到，再利用等量代换即可得出结论；
（2）连接，根据平行线的判定与性质得到，再根据等腰三角形的性质得到，，再由相似三角形的性质得到，再利用勾股定理进行计算即可．
【详解】（1）证明：∵为的直径，
∴，
∴，
∵是的切线，
∴，
∴，
∴，
∵，
∴，
∵，
∴；
（2）解：如图2，连接，
∵，
∴，
∴，
∵，
∴，
∴，
即，
∴，
∵，
∴，
∴，
∵，的半径为10，
∴，，
∴．

【点睛】本题考查切线的性质、圆周角定理、相似三角形的判定与性质、等腰三角形的性质、平行线的判定与性质及勾股定理，正确识别图形是解题的关键．
25．(1)，
(2)见解析
(3)
【分析】（1）先将点代入求得a的值，进而求得点C的坐标以及对称轴，再确定点B的坐标，然后运用待定系数法即可求得直线l的解析式；
（2）先用待定系数法求得直线的解析式为，则点、点、点，进而得到、，然后再根据三角形三边关系列不等式即可证明；
（3）由、C可得、；如图线段组成等腰三角形,与（2）中的相等，H为边上的高，再结合（2）可得；由等腰三角形的顶角是的2倍，即可得，然后再根据正弦的定义方程求解即可．
【详解】（1）解：∵抛物线经过点，
∴，解得：；
∴抛物线解析式为：，
令，得：，即点C的坐标为；
∵点，对称轴为直线，
∴，
∴点B的坐标为，
设直线的解析式为：,
∴，解得：，
∴直线的解析式为：，即直线l的解析式为．
故答案为，．
（2）解：设直线的解析式为,
∴，解得：，
∴直线的解析式为：；
∴点，点，点，
∴，
∴．
，
∴，
∴当时，线段总能组成等腰三角形．
（3）解：∵，C
∴
∴
如图：线段组成等腰三角形,与（2）中的相等，H为边上的高
由（2）可得：，
∴
∵等腰三角形的顶角是的2倍
∴
∴，
∴,即，解得：．
【点睛】本题主要考查了正弦函数、求二次函数解析式、二次函数的性质、用待定系数法求一次函数解析、等腰三角形的性质、勾股定理、坐标与图形等知识点，正确求得各函数的解析式是解答本题的关键．
26．(1)见解析
(2)
(3)
【分析】（1）边三角形与旋转的性质证明是等边三角形，得到，再证明，得，，从而得是等边三角形，得到，则有，即可得出结论；
（2）过点E作，交于H，连接，证是等边三角形，得到，不规则证明，得到，然后利用等边对等角和三角形内角和与外角性质求解即可；
（3）先求出，由折叠知，，则点是在以点E为圆心，为半径的上，再由旋转可知，，所以点G在以的中点为端点，与互相垂直平分的线段上，所以的最小值为，要使最小，则最大，又点F为上的点，所以点F在点D或点A时，最大，即最大，最大值为，即可求解．
【详解】（1）证明：∵是等边三角形，
∴，，即，
由旋转可得，，，
∴是等边三角形，
∴，
∴，
∴，
∴，，
∵，，
∴
∵为的中点，是等边三角形，，
∴，，
∴，
∴
∴是等边三角形，
∴，
∴
∴四边形是菱形；
（2）解：过点E作，交于H，连接，如图，
∵是等边三角形，
∴
∵
∴，，
∴是等边三角形，
∴，
由（1）可知，，
∵为的中点，等边三角形，
∴，
∵，
∴垂直平分，
∴，
∴，
设，则，，
∴
∵，，
∴，
∴，
∵，
∴，
∴，
∴；
（3）解：解：∵点E是的中点，
∴，
∴，
由折叠知，，
∴点是在以点E为圆心，为半径的上，
由旋转可知，，
∵点F为上的点，
∴点G在以的中点为端点，与互相垂直平分的线段上，
∴的最小值为，
要使最小，则最大，
∵点F为上的点，
∴点F在点D或点A时，最大，即最大，如图，
最大值为，
∴线段长度的最小值为．
【点睛】本题考查等边三角形的性质和判定，全等三角形的判定与性质，三角形内角和与外角性质，直角 三角形的性质，勾股定理，最短路径问题，本题属三角形综合题目，有一定难度，属中考试压轴题目，需要熟练掌握三角形相关知识，分析出最小值时，点F与点的位置是解题的关键．