2022-2023学年湖南省长沙市实验中学高一下学期期中数学试题

这是一份2022-2023学年湖南省长沙市实验中学高一下学期期中数学试题，文件包含湖南省长沙市实验中学高一下学期期中数学试题原卷版docx、湖南省长沙市实验中学高一下学期期中数学试题解析版docx等2份试卷配套教学资源，其中试卷共26页， 欢迎下载使用。
注意：本试卷共4页，22题，满分150分，时量：120分钟
一、选择题：本大题共8小题，每小题5分，共40分，在每小题给出的四个选项中，只有一项是符合题目要求的．
1. 已知集合，，则（ ）
A. B. C. D.
【答案】B
【解析】
【分析】由题得，再求.
【详解】由题得，所以.
故选：B
2. 已知复数，则z在复平面内对应的点位于（ ）
A. 第一象限B. 第二象限
C. 第三象限D. 第四象限
【答案】B
【解析】
【分析】计算出，则可选出答案.
【详解】，
所以复数z在复平面内对应的点为，在第二象限.
故选：B
3. 已知向量，，则（ ）
A. B. C. D.
【答案】A
【解析】
【分析】根据平面向量的坐标运算和向量共线、垂直的条件逐项进行检验即可求解.
【详解】对于A，因为，，所以，
则，所以，故选项A正确；
对于B，因为，，所以，则不存在实数λ使得，所以与不共线，故选项B错误；
对于C，因为，，且不存在实数λ使得，所以与不共线，故选项C错误；
对于D，因为，，且，所以与不垂直，故选项D错误；
故选：A.
4. 设非零实数满足，则下列不等式中一定成立的是
A. B. C. D.
【答案】D
【解析】
【分析】根据不等式的性质可得正确的选项.
【详解】取，则，故A错.
取，则，，故B、C错.
∵，∴．
故选：D．
【点睛】本题考查不等式的性质，说明一个不等式不成立，需举出反例，本题属于基础题.
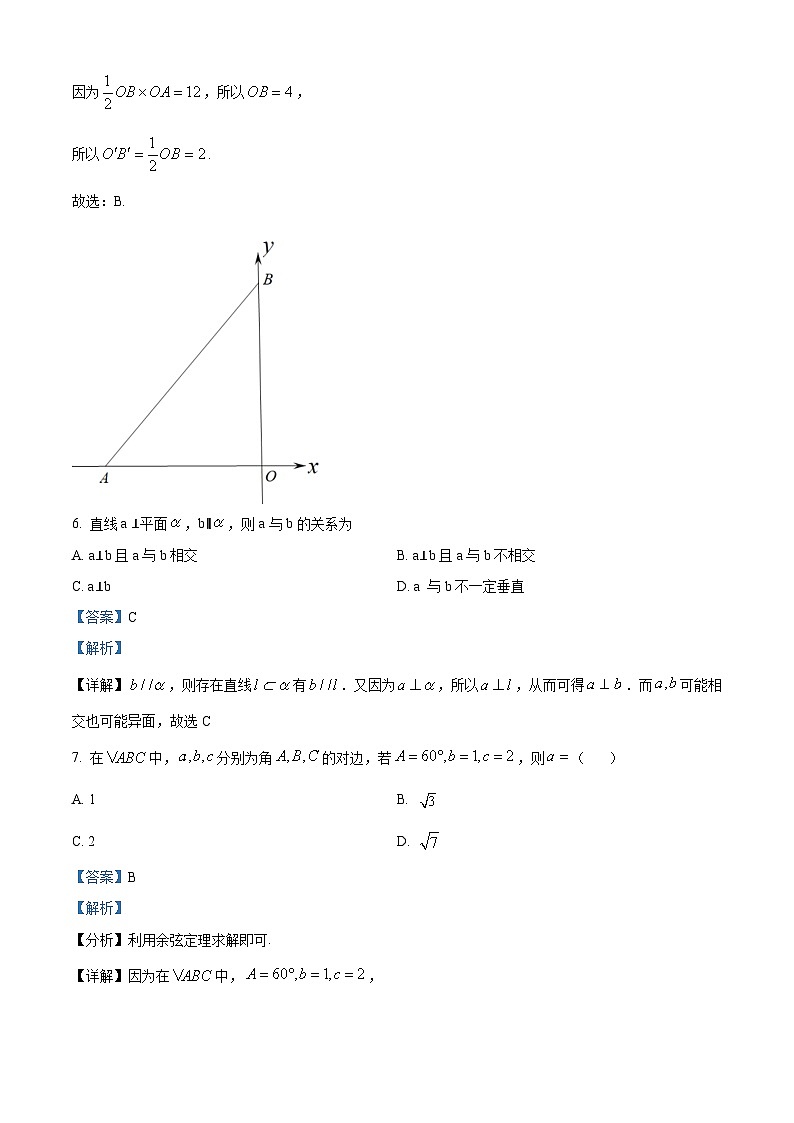
5. 如图，是水平放置的△AOB的直观图，但部分图象被茶渍覆盖，已知为坐标原点，顶点、均在坐标轴上，且△AOB的面积为12，则的长度为（ ）
A. 1B. 2C. 3D. 4
【答案】B
【解析】
【分析】画出△AOB的原图，根据三角形△AOB的面积为12可得答案.
【详解】画出△AOB的原图为直角三角形，且，
因为，所以，
所以.
故选：B.
6. 直线a ⊥平面，b∥，则a与b的关系为
A. a⊥b且a与b相交B. a⊥b且a与b不相交
C. a⊥bD. a 与b不一定垂直
【答案】C
【解析】
【详解】，则存在直线有．又因为，所以，从而可得．而可能相交也可能异面，故选C
7. 在中，分别为角的对边，若，则（ ）
A. 1B.
C. 2D.
【答案】B
【解析】
【分析】利用余弦定理求解即可.
【详解】因为在中，，
所以，解得：.
故选：B.
8. 平行四边形中，，，，点在边上，则的取值范围是（ ）
A. B. C. D.
【答案】C
【解析】
【分析】建立平面直角坐标系，设，把的取值范围转化为求二次函数的值域问题，即可求得本题答案.
【详解】作，垂足为，以点为原点，所在直线为轴，轴建立如下图的平面直角坐标系.
因为，而,所以，
在直角中，因为，，所以，，
则，设，
所以，
所以，
因为二次函数开口向上，对称轴为，且，
所以当时，取最小值，当时，取最大值，
所以的取值范围是.
故选：C
二、多选题（本题共4小题，每小题5分，共20分.在每小题给出的选项中有多项符合题目要求．全部选对的得5分，部分选对的得2分，有错选的得0分）
9. 下列关于复数的四个命题，其中为真命题的是（ ）
A. B. z的虚部为i
C. z的共轭复数为D.
【答案】AD
【解析】
【分析】根据复数的除法运算化简复数，即可结合选项逐一求解.
【详解】,故虚部为1，B错误；
其共轭复数为，C错误；
，A正确；
，故D正确，
故选：AD
10. 函数，下列说法正确的是（ ）
A. 为偶函数
B. 最小正周期为
C. 在区间上先减后增
D. 的图象关于对称
【答案】AC
【解析】
【分析】由题可得，然后结合函数的性质逐项分析即得.
【详解】由辅助角公式可得：，
对A，由题可知，为偶函数，A正确；
对B，最小正周期，故B错误；
对C，令，，在区间先减后增，故C正确；
对D，，所以关于点对称，D错误.
故选：AC．
11. 如图，在正方体中，、、分别是、、的中点，有下列四个结论正确的是（ ）
A. 与是异面直线；B. 、、相交于一点；
C. ；D. 平面.
【答案】BD
【解析】
【分析】本题首先可根据、判断出A错误，然后根据平面平面得出B正确，再然后根据得出C错误，最后根据线面平行的判定即可证得D正确.
【详解】A项：如图，连接、、，
因为、分别是、的中点，多面体是正方体，
所以，，，
因为，所以与是同一平面内的相交直线，A错误；
B项：因为平面平面，平面，平面，
所以、、相交于一点，B正确；
C项：如图，连接与交于点，连接、，
由正方体性质易知，是中点，
因为是中点，所以，，
因为，，所以，，
故四边形是平行四边形，，易知C错误；
D项：因为，平面，平面，
所以平面，D正确，
故选：BD.
12. “奔驰定理”因其几何表示酷似奔驰标志得来，是平面向量中一个非常优美的结论．奔驰定理与三角形四心（重心、内心、外心、垂心）有着神秘的关联．它的具体内容是：已知M是内一点，，，的面积分别为，，，且．以下命题正确的有（ ）
A. 若，则为的重心
B. 若为的内心，则
C. 若，，为的外心，则
D. 若为的垂心，，则
【答案】ABD
【解析】
【分析】对A，取BC的中点D，连接MD，AM，结合奔驰定理可得到，进而即可判断A；
对B，设内切圆半径为，从而可用表示出，，，再结合奔驰定理即可判断B；
对C，设的外接圆半径为，根据圆的性质结合题意可得，，，从而可用表示出，，，进而即可判断C；
对D，延长AM交BC于点D，延长BO交AC于点F，延长CO交AB于点E，根据题意结合奔驰定理可得到，，从而可设，，则，，代入即可求解，进而即可判断D．
【详解】对于A，取BC的中点D，连接MD，AM，
由，则，
所以，
所以A，M，D三点共线，且，
设E，F分别为AB，AC的中点，同理可得，，
所以为的重心，故A正确；
对于B，由为的内心，则可设内切圆半径为，
则有，，，
所以，
即，故B正确；
对于C，由为的外心，则可设的外接圆半径为，
又，，
则有，，，
所以，
，
，
所以，故C错误；
对于D，如图，延长AM交BC于点D，延长BM交AC于点F，延长CM交AB于点E，
由为的垂心，，则，
又，则，，
设，，则，，
所以，即，
所以，所以，故D正确；
故选：ABD．
【点睛】关键点点睛：解答D选项的关键是通过做辅助线（延长AM交BC于点D，延长BO交AC于点F，延长CO交AB于点E），根据题意，结合奔驰定理得到，，再设，，得到，，进而即可求解．
三、填空题（本题共4小题，每小题5分，共20分）
13. 化简： _______．
【答案】##
【解析】
【分析】利用两角差的正弦公式即可求解.
【详解】.
故答案：
14. 若一个圆锥的底面半径为1，其侧面展开图的圆心角大小为，则该圆锥的高为__________.
【答案】
【解析】
【分析】设圆锥的母线长为，由已知得，求得，由勾股定理可得解.
【详解】圆锥的底面半径为1，故圆锥的底面周长为，设圆锥的母线长为
根据圆锥的侧面展开图扇形的弧长等于圆锥底面周长可得：，解得：
所以圆锥的高
故答案为：
15. 写出使“不等式（且）对一切实数都成立”的的一个取值______．
【答案】（答案不唯一）
【解析】
【分析】由指数函数的单调性和不等式的性质，可得所求取值．
【详解】解：当时，在上单调递增，由，可得；
当时，在上单调递减，由，可得．
因为不等式对一切实数都成立，所以，
所以的取值可为．
故答案为：（答案不唯一）．
16. 如图，中，为边的中点，为线段上的任意一点（不含，），且，（x，），若恒成立，则实数a的最大值为_______．

【答案】8
【解析】
【分析】由题意易知，由此即可求出的最小值，即为a的最大值.
【详解】因为，，,三点共线，
则，
所以，
当且仅当，即时，取“=”.
所以的最大值为8.
故答案为：8
四、解答题（本题共6小题，共70分．解答应写出必要的文字说明、证明过程及演算步骤．）
17. 若函数的部分图象如下图所示.

（1）求函数的解析式；
（2）设，且，求的值.
【答案】（1），
（2）．
【解析】
【分析】（1）根据图象结合正弦函数图象及性质，即可求出；
（2）根据同角三角函数之间的关系求，再利用角的变换技巧，利用两角和的正弦公式即可求出.
【小问1详解】
由图得，．
，解得，
于是由，得．
所以，
因为函数图象过点，
所以
所以，
所以 ，即
又，所以，
所以．
【小问2详解】
因为，
所以，即，
因为，所以，
所以．
所以
=．
18. 在中，角所对的边分别为，且满足，．
（Ⅰ）求的面积；
（Ⅱ）若，求的值．
【答案】（1）；（2）.
【解析】
【分析】（1）利用二倍角公式由已知可得；根据向量的数量积运算，由得，再由三角形面积公式去求的面积；（2）由（1）知，又，解方程组可得或，再由余弦定理去求的值．
【详解】（1）因为，所以
又，所以，
由，得，所以
故的面积
（2）由，且，得或
由余弦定理得，故
考点：（1）二倍角公式及同角三角函数基本关系式；（2）余弦定理．
19. 如图，AB是半圆O的直径，C是半圆上一点，M是PB的中点，平面ABC，且，，.
（1）求证:平面PAC；
（2）求三棱锥M—ABC体积.
【答案】（1）证明见解析（2）2
【解析】
【分析】（1）依题意可得，再由平面，得到，即可证明平面；
（2）连接，可证，即可得到平面，为三棱锥的高，再根据锥体的体积公式计算可得；
【详解】（1）证明:因为是半圆的直径，所以.
因为平面，平面，所以，
又因为平面，平面，且
所以平面.
（2）解:因为，，所以，.连接.因为、分别是，的中点，所以，.又平面.所以平面.因此为三棱锥的高.所以.
【点睛】本题考查线面垂直的证明，锥体的体积的计算，属于中档题.
20. 如图所示，四边形EFGH为空间四边形ABCD的一个截面，若截面为平行四边形.
（1）求证：AB∥平面EFGH；
（2）若AB＝4，CD＝6，求四边形EFGH周长的取值范围.
【答案】（1）证明见解析
（2）(8，12)
【解析】
【分析】（1）通过证明平面，证得，由此证得平面.
（2）设，求得四边形周长的表达式，由此求得四边形周长的取值范围.
【小问1详解】
∵四边形EFGH为平行四边形，
∴EF∥HG.
∵HG⊂平面ABD，EF⊄平面ABD，
∴EF∥平面ABD.
又∵EF⊂平面ABC，平面ABD∩平面ABC＝AB，
∴EF∥AB，又∵AB⊄平面EFGH，EF⊂平面EFGH，
∴AB∥平面EFGH.
【小问2详解】
设，
∵EF∥AB，FG∥CD，∴，
则＝＝＝1－，∴.
∵四边形EFGH为平行四边形，
∴四边形EFGH的周长l＝2＝12－x.
又∵0