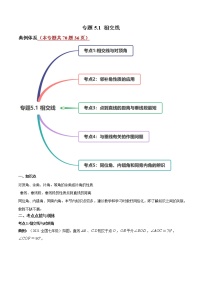
初中数学人教版七年级下册5.1.2 垂线练习题

这是一份初中数学人教版七年级下册5.1.2 垂线练习题，共12页。
理解垂直作为两条直线相交的特殊情形，掌握垂直的定义及性质；
理解并运用“垂线段最短”解决实际问题；
3.理解点到直线的距离的概念，并会度量点到直线的距离；
4.能依据对顶角、邻补角及垂直的概念与性质，进行简单的计算.
【知识要点】
1．垂线的定义：两条直线相交所成的四个角中，有一个角是直角时，就说这两条直线互相垂直，其中一条直线叫做另一条直线的垂线，它们的交点叫垂足．
特别说明：
(1)记法：直线a与b垂直，记作：；
直线AB和CD垂直于点O，记作：AB⊥CD于点O.
(2) 垂直的定义具有二重性，既可以作垂直的判定，又可以作垂直的性质，即有：
CD⊥AB．
2．垂线的画法：过一点画已知直线的垂线，可通过直角三角板来画，具体方法是使直角三角板的一条直角边和已知直线重合，沿直线左右移动三角板，使另一条直角边经过已知点，沿此直角边画直线，则所画直线就为已知直线的垂线(如图所示)．
特别说明：
(1)如果过一点画已知射线或线段的垂线时，指的是它所在直线的垂线，垂足可能在射线的反向延长线上，也可能在线段的延长线上．
(2)过直线外一点作已知直线的垂线，这点与垂足间的线段为垂线段．
3．垂线的性质：
（1）在同一平面内，过一点有且只有一条直线与已知直线垂直．
（2）连接直线外一点与直线上各点的所有线段中，垂线段最短．简单说成：垂线段最短．
特别说明：
（1）性质（1）成立的前提是在“同一平面内”，“有”表示存在，“只有”表示唯一，“有且只有”说明了垂线的存在性和唯一性．
（2）性质（2）是“连接直线外一点和直线上各点的所有线段中，垂线段最短．”实际上，连接直线外一点和直线上各点的线段有无数条，但只有一条最短，即垂线段最短．在实际问题中经常应用其“最短性”解决问题．
4．点到直线的距离：
定义：直线外一点到这条直线的垂线段的长度，叫做点到直线的距离．
特别说明：
点到直线的距离是垂线段的长度，是一个数量，不能说垂线段是距离；
（2）求点到直线的距离时，要从已知条件中找出垂线段或画出垂线段，然后计算或度量垂线段的长度．
【典型例题】
类型一、垂线➽➼定义的理解➼➻垂直✬✬直角
1．如图，直线，相交于点，下列条件：；；，其中能说明的有（ ）
A．B．或C．或D．或或
【答案】B
【分析】根据垂直定义“当两条直线相交所成的四个角中，有一个角是直角时，就说这两条直线互相垂直”进行判定即可．
解：，可以得出，故符合题意；
，，故符合题意，
，可以得出；
，不能得到，故不符合题意；
故能说明的有．
故选：B．
【点拨】此题主要考查了垂直定义，关键是通过条件计算出其中一个角为．
举一反三：
【变式1】如图，同一平面内的三条直线交于点O，，，AB与CD的关系是（ ）
A．平行B．垂直C．重合D．以上均有可能
【答案】B
【分析】由图知，∠1+∠2+∠AOC=180°，再由已知可得∠AOC=90°，从而可得AB与CD的位置关系．
∵∠1+∠2+∠AOC=180°，且，，
∴∠AOC=90°，
∴AB⊥CD，
∴AB与CD的位置关系是垂直．
故选：B．
【点拨】本题考查了垂直的定义，结合图形得到∠1+∠2+∠AOC=180°是本题的关键．
【变式2】如图，，则的度数是（ ）
A．B．C．D．
【答案】C
【分析】根据图象可得：∠1+∠2=90°，代入求解即可得出结果．
解：∵∠1+∠2+90°=180°，
∴∠1+∠2=90°，
∵∠1=20°，
∴∠2=70°，
故选：C．
【点拨】题目主要考查角度计算，从图中得出∠1+∠2=90°是解题关键．
类型二、垂线➽➼垂线的画法
2．如图，在纸片上有一直线l，点A在直线l上，过点A作直线l的垂线、嘉嘉使用了量角器，过90°刻度线的直线a即为所求；淇淇过点A将纸片折叠，使得以A为端点的两条射线重合，折痕a即为所求，下列判断正确的是（ ）
A．只有嘉嘉对B．只有淇淇对
C．两人都对D．两人都不对
【答案】C
【分析】根据垂直的定义即可解答．
解：嘉嘉利用量角器画90°角，可以画垂线，方法正确；
淇淇过点A将纸片折叠，使得以A为端点的两条射线重合，折痕a垂直直线l，方法正确，
故选：C．
【点拨】本题主要考查了作图、垂线的定义，掌握垂直的定义是解答本题的关键．
举一反三：
【变式1】 下列用三角板过点P画AB的垂线CD，正确的是（ ）
A．B．C．D．
【答案】D
【分析】根据垂线的作法，用直角三角板的一条直角边与重合，另一条直角边过点后沿直角边画直线即可．
解：根据分析可得，用直角三角板的一条直角边与重合，另一条直角边过点后沿直角边画直线，
选项的画法正确，
故选：．
【点拨】此题主要考查了垂线的画法，在平面内，过一点有且只有一条直线与已知直线垂直．
【变式2】过一条线段外一点，作这条线段的垂线，垂足在( )
A．这条线段上B．这条线段的端点处
C．这条线段的延长线上D．以上都可以
【答案】D
【分析】画一条线段的垂线就是画线段所在直线的垂线，进而得出答案.
解答：由垂线的定义知，画一条线段的垂线，垂足可以在线段上，可以是线段的端点，也可以在线段的延长线上.故选D.
【点拨】本题主要考查线段垂线的画法，正确把握垂线的定义是关键.
类型三、垂线➽➼点到直线的距离✬✬垂线段画法
3．如图，，P是OB上的一点，用刻度尺分别度量点P到直线OA和到直线OC的距离．
【答案】点P到直线OA的距离约为2cm，点P到直线OC的距离约为1.1cm
【分析】过点P作，用刻度尺分别度量PO和PD的长度，即可得到点P到直线OA和到直线OC的距离．
【详解】解：过点P作，用刻度尺分别度量，可得点P到直线OA的距离约为2cm，点P到直线OC的距离约为1.1cm．
【点拨】本题考查了点到直线的距离，解题的关键是清楚点到直线的距离是垂线段的长度．
举一反三：
【变式1】如图，、、相交于点，平分，，．
(1)线段______的长度表示点到的距离；
(2)比较与的大小（用“＜”号连接）：____________，并说明理由：____________；
(3)求的度数．
【答案】(1)；(2)，是因为垂线段最短；(3)
【分析】（1）根据点到直线的距离求解即可；
（2）根据垂线段最短求解即可；
（3）根据垂直的定义和角之间的关系求解即可．
（1）解：线段的长度表示点到的距离，
故答案为：；
（2）解：比较与的大小为：，是因为垂线段最短，
故答案为：，是因为垂线段最短；
（3）解：，平分，
，
．
【点拨】本题考查了点到直线的距离、角平分线、垂线段最短，解题的关键是掌握点到直线的距离．
【变式2】已知：点是直线外一点，点、、是直线上三点，分别连接、、．
（1）通过测量的方法，比较、、的大小，直接用“”连接；
（2）在直线上能否找到一点，使的长度最短？如果有，请在图中作出线段，并说明它的理论依据；如果没有，请说明理由．
【答案】（1）；（2）见解析，垂线段最短
【分析】(1)直接测量，比较大小即可；(2)作MN的垂线，垂足为D，PD即所求．
解：（1）通过测量可知，cm，cm，cm，
故；
（2）过点作，则最短．理由：垂线段最短

【点拨】本题考查了垂线段最短的性质，解题关键是能熟练的测量线段的长度，知道垂线段最短．
类型四、垂线➽➼点到直线的距离✬✬垂线段的长
4．如图，在中，，，，，点从点出发，沿射线以的速度运动，点从点出发，沿线段以的速度运动，、两点同时出发，当点运动到点时、停止运动，设点的运动时间为秒．
（1）当______时，；
（2）当______时，；
（3）画于点，并求出的值；
（4）当______时，有．
【答案】（1） （2）4或 （3）画图见解析； （4）
【分析】利用列方程得到，然后解方程即可；
利用列方程得到或，然后解方程即可；
先根据三角形高的定义画图，然后利用面积法求的长；
根据三角形面积公式得到，然后解方程即可．
解： 根据题意得，
解得；
故答案为：；
根据题意得或，
解得或；
故答案为：或；
如图，

，；
；
，
，
解得．
故答案为：．
【点拨】本题考查了三角形的面积以及求解一元一次方程，三角形的面积等于底边长与高线乘积的一半，能结合条件列出方程是解题的关键．
举一反三：
【变式1】 如图，点A、点B是直线l上两点，AB＝10，点M在直线l外，MB＝6，MA＝8，∠AMB＝90°，若点P为直线l上一动点，连接MP，则线段MP的最小值是____．
【答案】4.8
【分析】根据垂线段最短可知：当MP⊥AB时，MP有最小值，利用三角形的面积可列式计算求解MP的最小值．
解：当MP⊥AB时，MP有最小值，
∵AB＝10，MB＝6，MA＝8，∠AMB＝90°，
∴AB•MP＝AM•BM，
即10MP＝6×8，
解得MP＝4.8．
故答案为：4.8．
【点拨】本题主要考查垂线段最短，三角形的面积，找到MP最小时的P点位置是解题的关键．
【变式2】如图，在三角形ABC中，AC＝5，BC＝6，BC边上的高AD＝4，若点P在边AC上（不与点A，C重合）移动，则线段BP最短时的长为_________________．

【答案】
【分析】根据点到直线的连线中，垂线段最短，得到当BP垂直于AC时，BP的长最小，利用面积法即可求出此时BP的长．
解：根据垂线段最短可知，当BP⊥AC时，BP最短，
∵S△ABC＝×BC×AD＝×AC×BP，
∴6×4＝5BP，
∴PB＝，
即BP最短时的值为：．
故答案为：．
【点评】此题考查了垂线段最短，三角形的面积，熟练掌握线段的性质是解本题的关键．
中考真题专练
4．（2022·江苏常州·中考真题）如图，斑马线的作用是为了引导行人安全地通过马路．小丽觉得行人沿垂直马路的方向走过斑马线更为合理，这一想法体现的数学依据是（ ）
A．垂线段最短
B．两点确定一条直线
C．过一点有且只有一条直线与已知直线垂直
D．过直线外一点有且只有一条直线与已知直线平行
【答案】A
【分析】根据垂线段最短解答即可．
解：行人沿垂直马路的方向走过斑马线，体现的数学依据是垂线段最短，
故选：A．
【点拨】本题考查垂线段最短，熟知垂线段最短是解答的关键．
举一反三：
【变式1】 （2022·河南·中考真题）如图，直线AB，CD相交于点O，EO⊥CD，垂足为O．若∠1＝54°，则∠2的度数为（ ）
A．26°B．36°C．44°D．54°
【答案】B
【分析】根据垂直的定义可得，根据平角的定义即可求解．
解： EO⊥CD，
，
，
．
故选：B ．
【点拨】本题考查了垂线的定义，平角的定义，数形结合是解题的关键．
【变式2】（2021·北京·中考真题）如图，点在直线上，．若，则的大小为（ ）

A．B．C．D．
【答案】A
【分析】由题意易得，，进而问题可求解．
解：∵点在直线上，，
∴，，
∵，
∴，
∴；
故选A．
【点拨】本题主要考查垂直的定义及邻补角的定义，熟练掌握垂直的定义及邻补角的定义是解题的关键．
【变式3】（2021·浙江杭州·中考真题）如图，设点是直线外一点，，垂足为点，点是直线上的一个动点，连接，则（ ）
A．B．C．D．
【答案】C
【分析】根据垂线段距离最短可以判断得出答案．
【详解】解：根据点是直线外一点，，垂足为点，
是垂线段，即连接直线外的点与直线上各点的所有线段中距离最短，
当点与点重合时有，
综上所述：，
故选：C．
【点拨】本题考查了垂线段最短的定义，解题的关键是：理解垂线段最短的定义．