第5章 二次函数复习 苏科版九年级数学下册课件

这是一份第5章 二次函数复习 苏科版九年级数学下册课件，共28页。
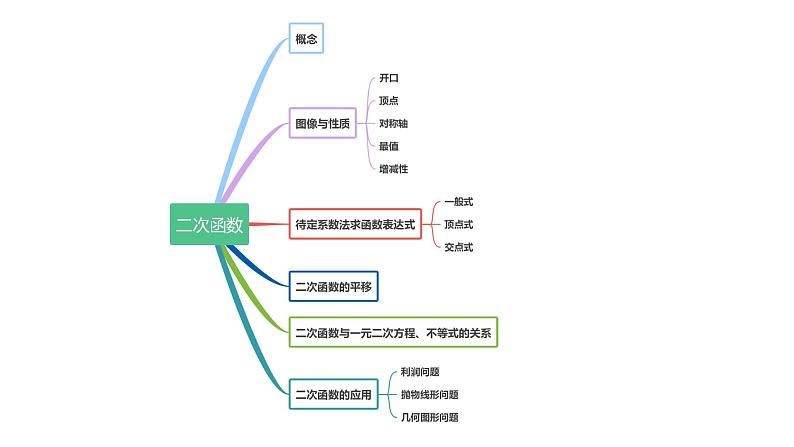
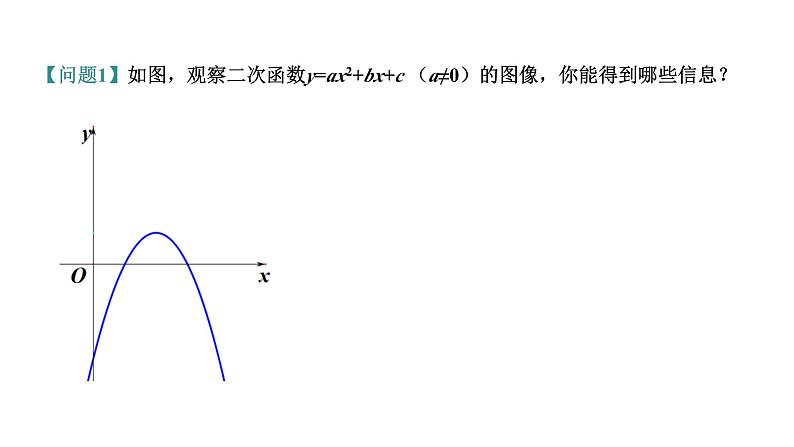
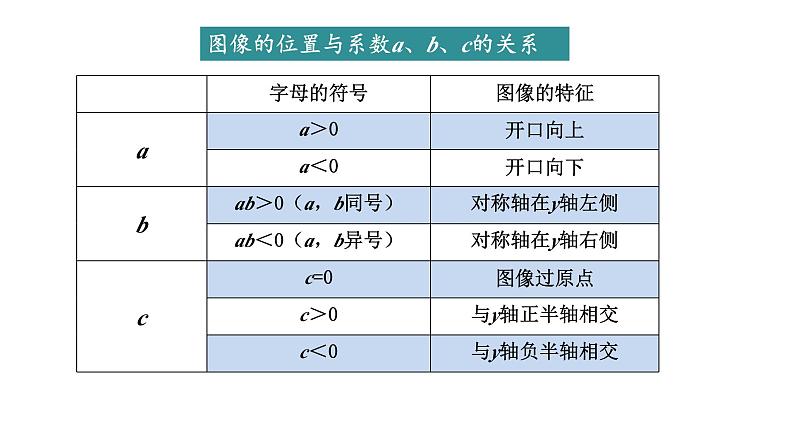
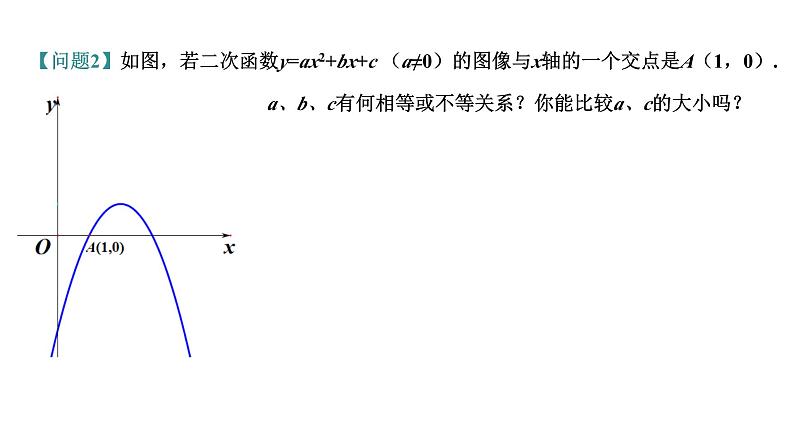
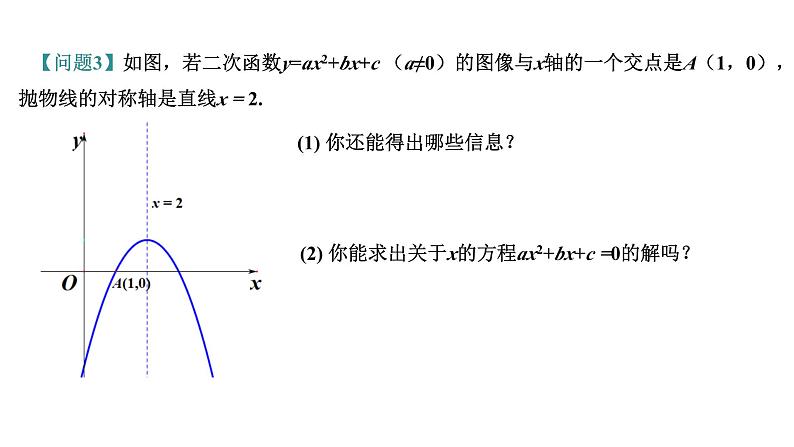
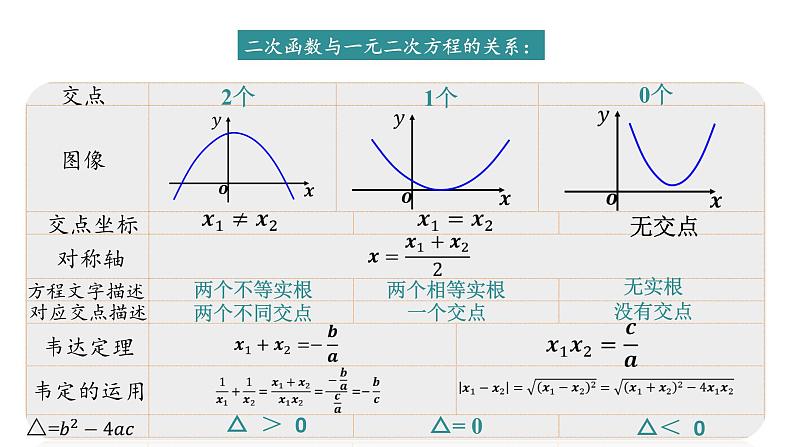
二次函数单元复习 【问题1】如图，观察二次函数y=ax2+bx+c （a≠0）的图像，你能得到哪些信息？图像的位置与系数a、b、c的关系 【问题2】如图，若二次函数y=ax2+bx+c （a≠0）的图像与x轴的一个交点是A（1，0）.a、b、c有何相等或不等关系？你能比较a、c的大小吗？ 【问题3】如图，若二次函数y=ax2+bx+c （a≠0）的图像与x轴的一个交点是A（1，0），抛物线的对称轴是直线x = 2. (1) 你还能得出哪些信息？(2) 你能求出关于x的方程ax2+bx+c =0的解吗？交点图像交点坐标对称轴方程文字描述对应交点描述韦达定理韦定的运用 2个1个0个  无交点 两个不等实根两个相等实根无实根两个不同交点一个交点没有交点    △ ＞ 0△= 0△＜ 0二次函数与一元二次方程的关系： (3)若点C(－3, y1)，D(－1, y2)，E(4, y3)，F(5, y4)是函数图像上的四个点，试比较y1、 y2、 y3、y4的大小关系. (4)若x ＜a时，y随x的增大而增大，求 a的取值范围. 【问题3】如图，若二次函数y=ax2+bx+c （a≠0）的图像与x轴的一个交点是A（1，0），抛物线的对称轴是直线x = 2.二次函数的图像与性质 【问题4】如图，若二次函数y=ax2+bx+c （a≠0）的图像与x轴的一个交点是A（1，0）,抛物线的对称轴是直线x = 2，抛物线与y轴的交点是C（0，－3）. (1) 你能求出二次函数的表达式吗？待定系数法求函数表达式基本步骤：函数表达式的选择：【问题5】如图，若二次函数y=ax2+bx+c （a≠0）的图像与x轴的一个交点是A（1，0）,抛物线的对称轴是直线x = 2，抛物线与y轴的交点是C（0，－3）. (1) 当0＜x＜1时，求y的取值范围. (2) 当1＜x＜4时，求y的取值范围. (3) 当y＞0时，求x的取值范围. (4) 当y＜-3时，求x的取值范围.二次函数与不等式 根的判别式△图像举例      2个1个无    无解无解二次函数与不等式的关系【问题6】如图，若二次函数y=ax2+bx+c （a≠0）的图像与x轴的一个交点是A（1，0）,抛物线的对称轴是直线x = 2，抛物线与y轴交于点C（0，－3）,直线l与抛物线交于点B、C. (1) 你能求出直线BC的表达式吗？ 【问题6】如图，若二次函数y=ax2+bx+c （a≠0）的图像与x轴的一个交点是A（1，0）,抛物线的对称轴是直线x = 2,抛物线与y轴的交点是C（0,－3）,直线l与抛物线交于点B、C. (2)若点P为直线BC上一点，点P到A 、 B两点的距离相等，将该抛物线向左（或向右）平移，得到一条新抛物线，并且新抛物线经过点P，求新抛物线的顶点坐标.二次函数的平移 (3) 若点M是线段BC上的一点，过点M作x轴的垂线，交抛物线于点N，求线段MN的最大值.二次函数中的最值【问题6】如图，若二次函数y=ax2+bx+c （a≠0）的图像与x轴的一个交点是A（1，0）,抛物线的对称轴是直线x = 2，抛物线与y轴交于点C（0，－3）,直线l与抛物线交于点B、C. (4) 若点M是线段BC上的一点，过点M作x轴的垂线，交抛物线于点N，过点N作NH⊥BC，求线段NH的最大值.二次函数中的最值【问题6】如图，若二次函数y=ax2+bx+c （a≠0）的图像与x轴的一个交点是A（1，0）,抛物线的对称轴是直线x = 2，抛物线与y轴交于点C（0，－3）,直线l与抛物线交于点B、C.化斜为直 (5) 若点M是线段BC上的一点，过点M作x轴的垂线，交抛物线于点N，过点N作NH⊥BC，求△MNH周长的最大值.二次函数中的最值【问题6】如图，若二次函数y=ax2+bx+c （a≠0）的图像与x轴的一个交点是A（1，0）,抛物线的对称轴是直线x = 2，抛物线与y轴交于点C（0，－3）,直线l与抛物线交于点B、C. (1) 抛物线是否存在点N使得△NBC面积与△ABC的面积相等？若存在，求出点N的坐标.二次函数中的面积【问题7】如图，若二次函数y=ax2+bx+c （a≠0）的图像与x轴的一个交点是A（1，0）,抛物线的对称轴是直线x = 2，抛物线与y轴交于点C（0，－3）,直线l与抛物线交于点B、C. (2) 若点N是直线BC上方抛物线上一点，求△NBC面积的最大值.二次函数中的面积【问题7】如图，若二次函数y=ax2+bx+c （a≠0）的图像与x轴的一个交点是A（1，0）,抛物线的对称轴是直线x = 2，抛物线与y轴交于点C（0，－3）,直线l与抛物线交于点B、C. (2) 若点N是直线BC上方抛物线上一点，求△NBC面积的最大值.二次函数中的面积【问题7】如图，若二次函数y=ax2+bx+c （a≠0）的图像与x轴的一个交点是A（1，0）,抛物线的对称轴是直线x = 2，抛物线与y轴交于点C（0，-3）,直线l与抛物线交于点B、C. 若点N是直线BC上方抛物线上一点，是否存在点N使得△NBC是以BC为底的等腰三角形？若存在，求出点N的坐标.二次函数中的等腰三角形存在性【问题8】如图，若二次函数y=ax2+bx+c （a≠0）的图像与x轴的一个交点是A（1，0）,抛物线的对称轴是直线x = 2，抛物线与y轴交于点C（0，－3）,直线l与抛物线交于点B、C.二次函数中的平行四边形存在性 过点C作x轴的平行线，交抛物线于点D，点 M在抛物线上，点 N在抛物线在对称轴上，是否存在以A、D、M、N为顶点的四边形是平行四边形？若存在，直接写出所有符合条件的点M的坐标.【问题9】如图，若二次函数y=ax2+bx+c （a≠0）的图像与x轴的一个交点是A（1，0）,抛物线的对称轴是直线x = 2，抛物线与y轴交于点C（0，－3）,直线l与抛物线交于点B、C.二次函数中的等角存在性 M为抛物线上一点，是否存在∠ACM = ∠OCB ？若存在，求出点M的坐标.【问题10】如图，若二次函数y=ax2+bx+c （a≠0）的图像与x轴的一个交点是A（1，0）,抛物线的对称轴是直线x = 2，抛物线与y轴交于点C（0，－3）,直线l与抛物线交于点B、C.二次函数中的等角存在性 M为抛物线上一点，是否存在∠ACM = ∠OCB ？若存在，求出点M的坐标.【问题10】如图，若二次函数y=ax2+bx+c （a≠0）的图像与x轴的一个交点是A（1，0）,抛物线的对称轴是直线x = 2，抛物线与y轴交于点C（0，－3）,直线l与抛物线交于点B、C.二次函数中的等角存在性 M为抛物线上一点，是否存在∠ACM = ∠OCB ？若存在，求出点M的坐标.【问题10】如图，若二次函数y=ax2+bx+c （a≠0）的图像与x轴的一个交点是A（1，0）,抛物线的对称轴是直线x = 2，抛物线与y轴交于点C（0，－3）,直线l与抛物线交于点B、C.同学们，再见！