




还剩11页未读,
继续阅读
第5章 走进图形世界 苏科版数学七年级上册课件
展开
这是一份第5章 走进图形世界 苏科版数学七年级上册课件,共19页。
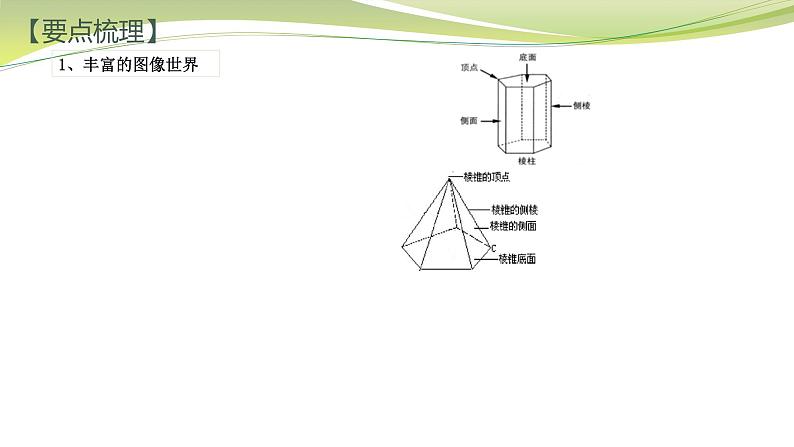
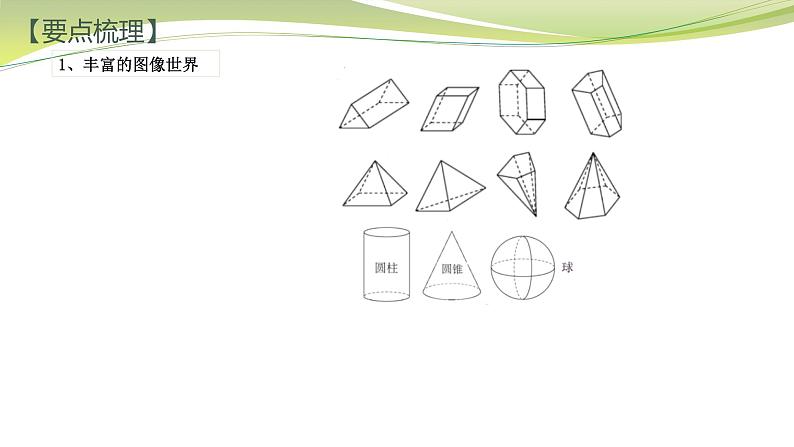
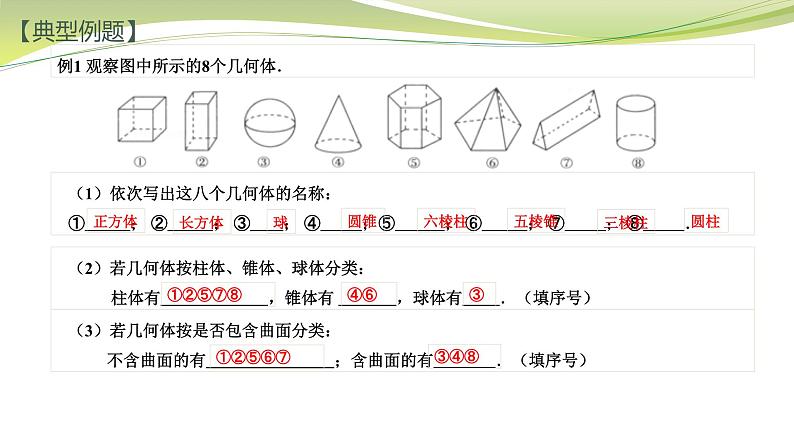
走进图形世界【要点梳理】1、丰富的图像世界【要点梳理】1、丰富的图像世界【要点梳理】3、展开与折叠 立体图形与平面图形之间的关系:有些立体图形可以按不同的方式展开成平面图形,有些平面图形也可以折叠成立体图形.4、三视图 从正面看到的图形称为主视图;从左面看到的图形称为左视图;从上面看到的图形称为俯视图.2、图形的运动点动成线,线动成面,面动成体.图形的运动:平移、旋转、翻折.运用平移、旋转、翻折,让图形“动”起来,是研究图形性质的重要方法.【典型例题】例1 观察图中所示的8个几何体.(1)依次写出这八个几何体的名称:① ; ② ; ③ ; ④ ;⑤ ; ⑥ ; ⑦ ; ⑧ .(2)若几何体按柱体、锥体、球体分类: 柱体有 ,锥体有 ,球体有 .(填序号)(3)若几何体按是否包含曲面分类: 不含曲面的有 ;含曲面的有 .(填序号)正方体长方体球圆锥六棱柱五棱锥圆柱三棱柱①②⑤⑦⑧④⑥③①②⑤⑥⑦③④⑧【典型例题】例2 (1)如图所示的五棱柱有多少个面?多少条棱?多少个顶点?十棱柱有几个面?几条棱?几个顶点?解:(1)五棱柱有7个面,15条棱,10个顶点; 十棱柱有12个面,30条棱,20个顶点.【典型例题】例2 (1)如图所示的五棱柱有多少个面?多少条棱?多少个顶点?十棱柱有几个面?几条棱?几个顶点?(2)若如图所示的是直五棱柱,它的底面边长都是5cm,侧棱长12cm,则它的所有侧面的面积之和是多少?解:(2)直五棱柱所有侧面的面积之和是:5×12×5=300(cm2).答:直五棱柱所有侧面的面积之和是300cm2.【典型例题】例2 (3)①三棱锥有 条棱,四棱锥有 条棱,五棱锥有 条棱. ② 棱锥有30条棱. ③若一个棱锥有100棱,则这个棱锥是 棱锥,共有 个面.解:(3)①三棱锥侧面有3条棱,底面有3条棱,共有6条棱,6 四棱锥侧面有4条棱,底面有4条棱,共有8条棱,8 五棱锥侧面有5条棱,底面有5条棱,共有10条棱;10 ②若一个棱锥有30条棱,则底面有15条棱,是十五棱锥;十五 ③若一个棱锥有100条棱,则底面有50条棱,为五十棱锥,共有51个面.五十51【典型例题】例3 如图所示,依次写出展开后的5种平面图对应的几何体的名称. (1) ;(2) ;(3) ;(4) ;(5) .正方体长方体三棱柱四棱锥圆柱【典型例题】例4某综合实践小组进行废物再利用的环保小卫士行动.他们准备用废弃的宣传单制作装垃圾的无盖纸盒.(1)若准备制作一个无盖的正方体形纸盒,图1中经过折叠能围成无盖正方体形纸盒的图形是( )C(2)如图2是小明的设计图,把它折成无盖正方体形纸盒后与“保”相对的字是 ;卫 如图是图1中的C图,折成无盖正方体形纸盒后与“保”相对的字是 ;士【典型例题】例4某综合实践小组进行废物再利用的环保小卫士行动.他们准备用废弃的宣传单制作装垃圾的无盖纸盒.(3)如图3,有一张边长为20cm的正方形废弃宣传单,小华准备将其四角各剪去一个小正方形,折成无盖长方体形纸盒. ①请你在图3中画出示意图,用实线表示剪切线,虚线表示折痕.解:(3)①如图所示:②若四角各剪去了一个边长为xcm的小正方形,用含x的代数式表示这个纸盒的高为 cm,底面积 为 cm2,当小正方形边长为4cm时,求纸盒的容积. ②当小正方形边长为4cm,即x=4时, 纸盒的容积为x(20﹣2x)2=4×(20﹣2×4)2=4×122=576(cm3).x(20﹣2x)2【典型例题】例5 (1)由若干个相同的小立方体搭成的一个几何体的主视图和俯视图如图所示,俯视图的方格中的字母和数字表示该位置上小立方体的个数,则x+y= .解:(1)根据俯视图上所标出的数字,结合主视图,可得x=1或x=2,而y=3, 因此 x+y=1+3=4 或 x+y=2+3=5.4或5【典型例题】例5 (1)由若干个相同的小立方体搭成的一个几何体的主视图和俯视图如图所示,俯视图的方格中的字母和数字表示该位置上小立方体的个数,则x+y= .4或5 (2)如图,这是一个由一些相同的小正方体搭成的几何体俯视图,小正方形中的数字表示该位置的小立方块的个数.请你画出它的主视图和左视图.解:(2)如图所示: 【典型例题】例5 (3)如图,是由若干个棱长为1的小正方体组成的一个几何体.①请画出这个几何体的从左面看和从上面看到的形状图(用阴影表示)解:(3)①如图所示:【典型例题】例5 (3)如图,是由若干个棱长为1的小正方体组成的一个几何体.③再用与原来一样的小正方体在旁边搭一个几何体,使所搭几何体恰好与图2中的几何体拼成一个无缝隙的大长方体(不改变原来几何体的形状),那么至少还需要 个小正方体,所搭几何体的表面积为 .1748解:由题可知,最小的大正方体是由小方块组成的3×3×3的大正方体, 根据题意得到题中堆积体的俯视图,并进行标数: 所以按照要求搭几何体至少需要27﹣10=17个小立方体. 由图中的俯视图可知,能将其补充为完整的3×3×3的大正方体的剩余部分的俯视图为: 由此可得,所做堆积体的三视图,主、左、俯三视图面积皆为8, 所以所搭几何体的表面积为(8+8+8)×2=48,【课后检测】例6(1)用小立方体搭成一个几何体,使它的主视图和俯视图如图所示.搭建这样的几何体,最多 要 个小立方体,最少要 个小立方体.解:(1)由主视图可知,它自下而上共有3列:第一列3块,第二列3块,第三列1块; 由俯视图可知,它自左而右共有3列:第一列3块,第二列3块,第三列1块,从空中俯视 的块数只要最低层有一块即可. 因此,综合两图可知这个几何体的形状不能确定,并且最少时为第一列中有一个三层, 其余为一层,第二列中有一个三层,另一个为一层,第三列一层,共11块,如图;1711 最多要17块,如图.【课后检测】例6(2)如图为一个用正方体积木搭成的几何体的三视图,俯视图中方格上的数字表示该位置上积 木累积的个数.若保证正视图和左视图成立,则a+b+c+d的最大值为 .解:(2)由正视图第1列和左视图第1列可知a最大为3, 由正视图第2列和左视图第2列可知b最大为3, 由正视图第3列和左视图第1列和第2列可知c最大为4,d最大为3, 则 a+ b+ c+ d的最大值为3+3+4+3=13.13【课后检测】例6(3)已知一个物体由x个相同的小正方体堆成,它的正视图和左视图如图所示,那么x的最大值 与最小值的差是 .解:(3)底面最多有9个小正方体,第二层最多有2个小正方体,那么x的最大值应该是9+2=11;5 底面最少有4个小正方体,第二层最少有2个小正方体,那么x的最小值应该是4+2=6. 故 x的最大值与最小值的差是11﹣6=5.谢谢收看!
走进图形世界【要点梳理】1、丰富的图像世界【要点梳理】1、丰富的图像世界【要点梳理】3、展开与折叠 立体图形与平面图形之间的关系:有些立体图形可以按不同的方式展开成平面图形,有些平面图形也可以折叠成立体图形.4、三视图 从正面看到的图形称为主视图;从左面看到的图形称为左视图;从上面看到的图形称为俯视图.2、图形的运动点动成线,线动成面,面动成体.图形的运动:平移、旋转、翻折.运用平移、旋转、翻折,让图形“动”起来,是研究图形性质的重要方法.【典型例题】例1 观察图中所示的8个几何体.(1)依次写出这八个几何体的名称:① ; ② ; ③ ; ④ ;⑤ ; ⑥ ; ⑦ ; ⑧ .(2)若几何体按柱体、锥体、球体分类: 柱体有 ,锥体有 ,球体有 .(填序号)(3)若几何体按是否包含曲面分类: 不含曲面的有 ;含曲面的有 .(填序号)正方体长方体球圆锥六棱柱五棱锥圆柱三棱柱①②⑤⑦⑧④⑥③①②⑤⑥⑦③④⑧【典型例题】例2 (1)如图所示的五棱柱有多少个面?多少条棱?多少个顶点?十棱柱有几个面?几条棱?几个顶点?解:(1)五棱柱有7个面,15条棱,10个顶点; 十棱柱有12个面,30条棱,20个顶点.【典型例题】例2 (1)如图所示的五棱柱有多少个面?多少条棱?多少个顶点?十棱柱有几个面?几条棱?几个顶点?(2)若如图所示的是直五棱柱,它的底面边长都是5cm,侧棱长12cm,则它的所有侧面的面积之和是多少?解:(2)直五棱柱所有侧面的面积之和是:5×12×5=300(cm2).答:直五棱柱所有侧面的面积之和是300cm2.【典型例题】例2 (3)①三棱锥有 条棱,四棱锥有 条棱,五棱锥有 条棱. ② 棱锥有30条棱. ③若一个棱锥有100棱,则这个棱锥是 棱锥,共有 个面.解:(3)①三棱锥侧面有3条棱,底面有3条棱,共有6条棱,6 四棱锥侧面有4条棱,底面有4条棱,共有8条棱,8 五棱锥侧面有5条棱,底面有5条棱,共有10条棱;10 ②若一个棱锥有30条棱,则底面有15条棱,是十五棱锥;十五 ③若一个棱锥有100条棱,则底面有50条棱,为五十棱锥,共有51个面.五十51【典型例题】例3 如图所示,依次写出展开后的5种平面图对应的几何体的名称. (1) ;(2) ;(3) ;(4) ;(5) .正方体长方体三棱柱四棱锥圆柱【典型例题】例4某综合实践小组进行废物再利用的环保小卫士行动.他们准备用废弃的宣传单制作装垃圾的无盖纸盒.(1)若准备制作一个无盖的正方体形纸盒,图1中经过折叠能围成无盖正方体形纸盒的图形是( )C(2)如图2是小明的设计图,把它折成无盖正方体形纸盒后与“保”相对的字是 ;卫 如图是图1中的C图,折成无盖正方体形纸盒后与“保”相对的字是 ;士【典型例题】例4某综合实践小组进行废物再利用的环保小卫士行动.他们准备用废弃的宣传单制作装垃圾的无盖纸盒.(3)如图3,有一张边长为20cm的正方形废弃宣传单,小华准备将其四角各剪去一个小正方形,折成无盖长方体形纸盒. ①请你在图3中画出示意图,用实线表示剪切线,虚线表示折痕.解:(3)①如图所示:②若四角各剪去了一个边长为xcm的小正方形,用含x的代数式表示这个纸盒的高为 cm,底面积 为 cm2,当小正方形边长为4cm时,求纸盒的容积. ②当小正方形边长为4cm,即x=4时, 纸盒的容积为x(20﹣2x)2=4×(20﹣2×4)2=4×122=576(cm3).x(20﹣2x)2【典型例题】例5 (1)由若干个相同的小立方体搭成的一个几何体的主视图和俯视图如图所示,俯视图的方格中的字母和数字表示该位置上小立方体的个数,则x+y= .解:(1)根据俯视图上所标出的数字,结合主视图,可得x=1或x=2,而y=3, 因此 x+y=1+3=4 或 x+y=2+3=5.4或5【典型例题】例5 (1)由若干个相同的小立方体搭成的一个几何体的主视图和俯视图如图所示,俯视图的方格中的字母和数字表示该位置上小立方体的个数,则x+y= .4或5 (2)如图,这是一个由一些相同的小正方体搭成的几何体俯视图,小正方形中的数字表示该位置的小立方块的个数.请你画出它的主视图和左视图.解:(2)如图所示: 【典型例题】例5 (3)如图,是由若干个棱长为1的小正方体组成的一个几何体.①请画出这个几何体的从左面看和从上面看到的形状图(用阴影表示)解:(3)①如图所示:【典型例题】例5 (3)如图,是由若干个棱长为1的小正方体组成的一个几何体.③再用与原来一样的小正方体在旁边搭一个几何体,使所搭几何体恰好与图2中的几何体拼成一个无缝隙的大长方体(不改变原来几何体的形状),那么至少还需要 个小正方体,所搭几何体的表面积为 .1748解:由题可知,最小的大正方体是由小方块组成的3×3×3的大正方体, 根据题意得到题中堆积体的俯视图,并进行标数: 所以按照要求搭几何体至少需要27﹣10=17个小立方体. 由图中的俯视图可知,能将其补充为完整的3×3×3的大正方体的剩余部分的俯视图为: 由此可得,所做堆积体的三视图,主、左、俯三视图面积皆为8, 所以所搭几何体的表面积为(8+8+8)×2=48,【课后检测】例6(1)用小立方体搭成一个几何体,使它的主视图和俯视图如图所示.搭建这样的几何体,最多 要 个小立方体,最少要 个小立方体.解:(1)由主视图可知,它自下而上共有3列:第一列3块,第二列3块,第三列1块; 由俯视图可知,它自左而右共有3列:第一列3块,第二列3块,第三列1块,从空中俯视 的块数只要最低层有一块即可. 因此,综合两图可知这个几何体的形状不能确定,并且最少时为第一列中有一个三层, 其余为一层,第二列中有一个三层,另一个为一层,第三列一层,共11块,如图;1711 最多要17块,如图.【课后检测】例6(2)如图为一个用正方体积木搭成的几何体的三视图,俯视图中方格上的数字表示该位置上积 木累积的个数.若保证正视图和左视图成立,则a+b+c+d的最大值为 .解:(2)由正视图第1列和左视图第1列可知a最大为3, 由正视图第2列和左视图第2列可知b最大为3, 由正视图第3列和左视图第1列和第2列可知c最大为4,d最大为3, 则 a+ b+ c+ d的最大值为3+3+4+3=13.13【课后检测】例6(3)已知一个物体由x个相同的小正方体堆成,它的正视图和左视图如图所示,那么x的最大值 与最小值的差是 .解:(3)底面最多有9个小正方体,第二层最多有2个小正方体,那么x的最大值应该是9+2=11;5 底面最少有4个小正方体,第二层最少有2个小正方体,那么x的最小值应该是4+2=6. 故 x的最大值与最小值的差是11﹣6=5.谢谢收看!
相关资料
更多









