第7章 平面图形的认识（二）复习 苏科版数学七年级下册课件

这是一份第7章 平面图形的认识（二）复习 苏科版数学七年级下册课件，共38页。

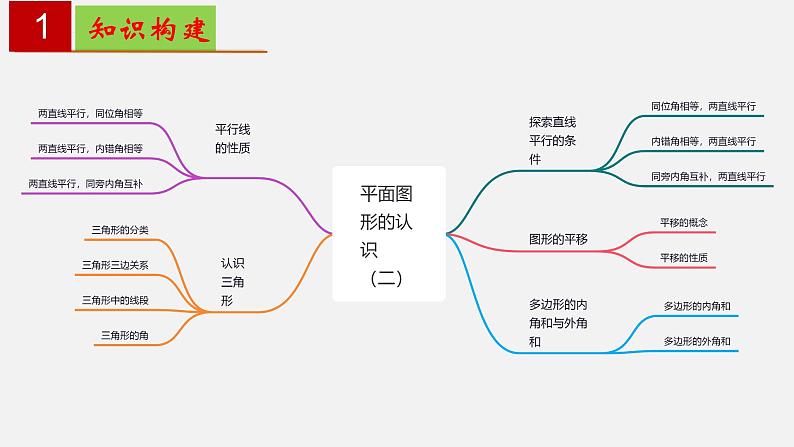
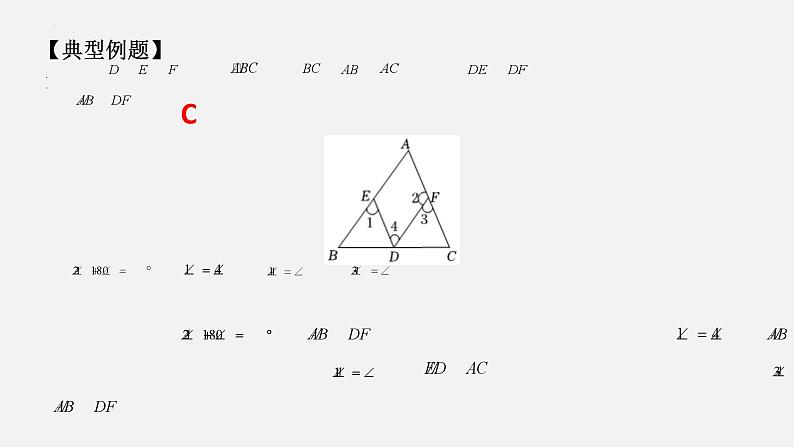
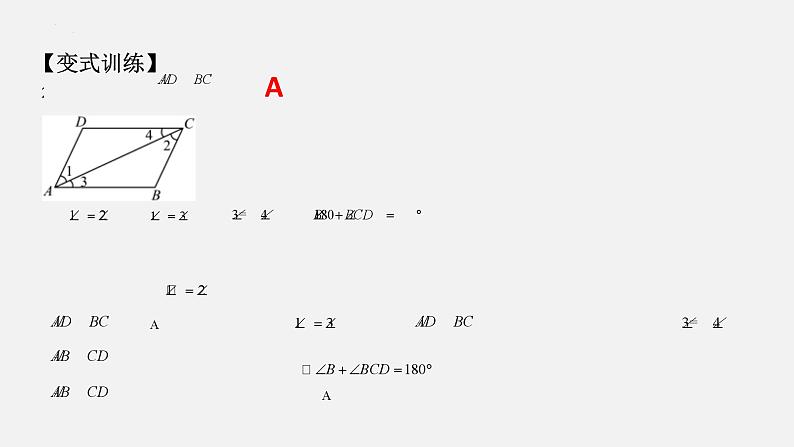
苏科版七年级下册第7章 平面图形的认识（二） 知识构建 1复习目标复习重点平行线的判定与性质，图形平移的性质以及三角形的三边关系。 复习目标 21. 区别平行线的判定与性质，并能灵活运用；2. 了解图形平移的概念及性质；3. 熟练掌握三角形的三边关系及内角和定理，并能灵活应用；4、掌握多边形的内角和公式与外角和定理． 重难点突破 3知识点一 平行线的判定与性质平行线的判定与性质平行线的判定判定方法1：同位角相等，两直线平行判定方法2：内错角相等，两直线平行判定方法3：同旁内角互补，两直线平行          根据平行线的定义和平行公理的推论，平行线的判定方法还有：平行线的定义：在同一平面内，如果两条直线没有交点（不相交），那么两直线平行.如果两条直线都平行于第三条直线，那么这两条直线平行（平行线的传递性）.在同一平面内，垂直于同一直线的两条直线平行.平行公理：经过直线外一点，有且只有一条直线与这条直线平行. 重难点突破 4知识点一 平行线的判定与性质平行线的判定与性质平行线的性质性质1：两直线平行，同位角相等；性质2：两直线平行，内错角相等；性质3：两直线平行，同旁内角互补。          根据平行线的定义和平行公理的推论，平行线的性质还有：若两条直线平行，则这两条直线在同一平面内，且没有公共点。如果一条直线与两条平行线中的一条直线垂直，那么它必与另一条直线垂直。【典型例题】C【变式训练】C【变式训练】A【典型例题】B【变式训练】B【变式训练】D知识点二 图形的平移平移的定义在平面内，将一个图形沿某个方向移动一定的距离，图形的这种移动叫做平移。决定平移的两个要素：平移的方向；平移的距离；平移的方向      平移的距离知识点二 图形的平移平移的性质：1.图形的平移不改变图形的形状与大小，只改变图形的位置．2.图形平移后，对应点的连线平行或在同一直线上且相等．3.图形经过平移，对应线段互相平行或在同一条直线上且相等，对应角相等．      【典型例题】A【变式训练】D【变式训练】A【典型例题】【变式训练】【变式训练】知识点三 认识三角形 三角形的分类锐角三角形直角三角形按角分三角形的任意两边之和大于第三边; 三角形任意两边之差小于第三边。判断给定三条线段能否构成一个三角形：看较小两边的和是否大于最长边。已知三角形的两边长,确定第三边的范围：两边之差的绝对值＜第三边＜两边之和。钝角三角形不等边三角形等边三角形按边分底和腰不等的等腰三角形等腰三角形三角形的三边关系知识点三 认识三角形 三角形的三条主要线段在三角形中，连接一个顶点与它对边中点的线段，叫做三角形的中线。三角形的三条中线交于三角形内部一点，叫做三角形的重心。在三角形中，一个内角的平分线与它的对边相交，这个角的顶点与交点之间的线段叫做三角形的角平分线，三角形的三条角平分线交于三角形内一点，叫做三角形的内心。在三角形中，从一个顶点向它的对边所在直线作垂线，顶点与垂足之间的线段叫做三角形的高线，简称三角形的高，三角形的三条高交于一点，叫做三角形的垂心。      知识点三 认识三角形 三角形的角三角形的内角和为180°。三角形的一边与他的邻边的延长线组成的角叫做三角形的外角。      1.直角三角形的两个锐角互余；2.三角形的一个外角等于与它不相邻的两内角和；3.三角形的一个外角大于任意一个不相邻的内角。【典型例题】D【变式训练】A【变式训练】B【典型例题】B【变式训练】A【变式训练】A 重难点突破 5知识点四 多边形的内角和与外角和 多边形的内角和n边形的内角和为(n-2)·180°（n≥3）内角和定理的应用：①已知多边形的边数，求其内角和；②已知多边形内角和求其边数；正多边形的每个内角都相等，都等于 多边形的外角和:任意多边形的外角和都为360°。多边形的外角和为360°．n边形的外角和恒等于360°，它与边数的多少无关.【典型例题】【变式训练】【变式训练】【典型例题】【变式训练】【变式训练】易错易混易错易混单元小结