初中数学华师大版九年级下册2. 圆的对称性教学演示课件ppt

这是一份初中数学华师大版九年级下册2. 圆的对称性教学演示课件ppt，共23页。PPT课件主要包含了情境引入，导入新课，探究归纳，用折叠的方法，圆的对称性，在同圆中探究，③ABCD，不可以如图，在等圆中探究，在同圆或等圆中等内容，欢迎下载使用。
熊宝宝要过生日了！要把蛋糕平均分成四块，你会分吗？
问题1 圆是轴对称图形吗？如果是，它的对称轴是 什么？你能找到多少条对称轴？
问题2 你是怎么得出结论的？
圆的对称性： 圆是轴对称图形，其对称轴是任意一条过圆心的直线.
问题3 将圆绕圆心旋转 180° 后，得到的图形与原图形重合吗？由此你得到什么结论呢？
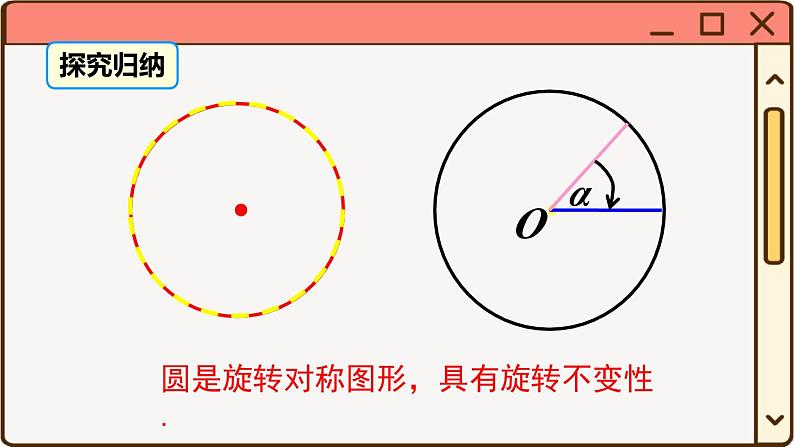
我们探索发现圆是一个旋转对称图形，绕圆心旋转 180 度还是多少度后，它都能与自身重合，对称中心即为圆心.
圆是旋转对称图形，具有旋转不变性.
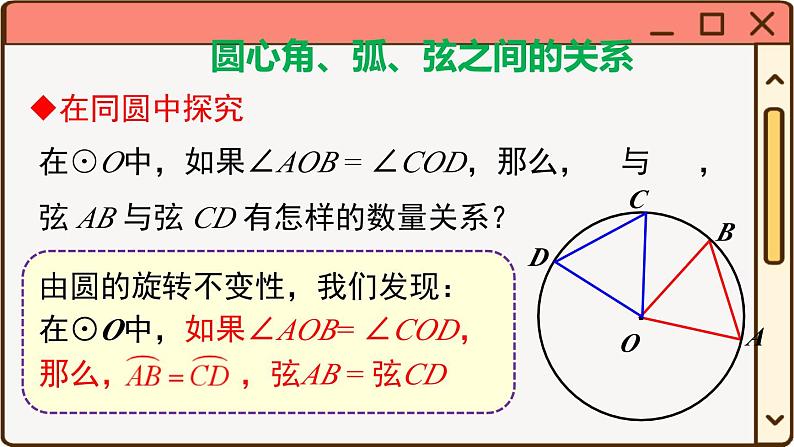
由圆的旋转不变性，我们发现：在⊙O中，如果∠AOB= ∠COD，那么， ，弦AB = 弦CD
圆心角、弧、弦之间的关系
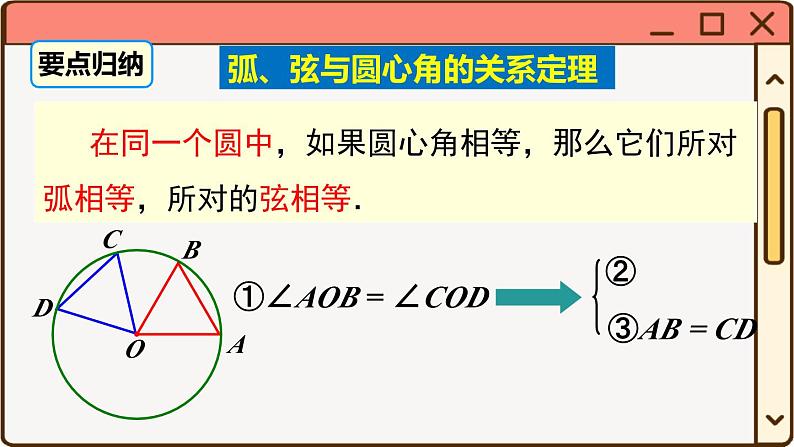
在同一个圆中，如果圆心角相等，那么它们所对弧相等，所对的弦相等．
①∠AOB = ∠COD
弧、弦与圆心角的关系定理
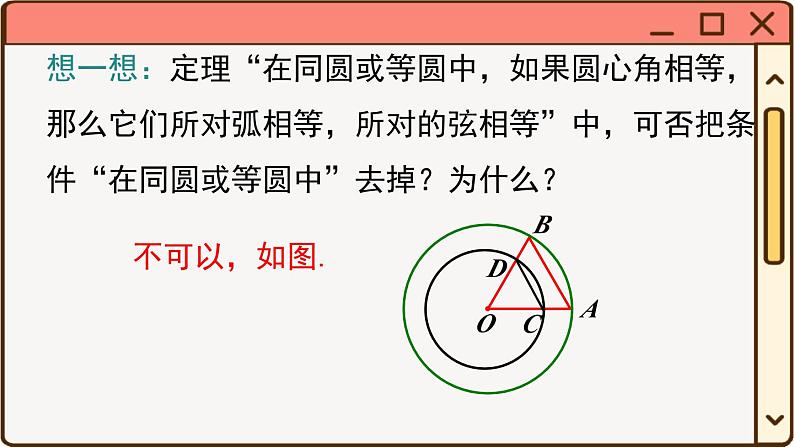
想一想：定理“在同圆或等圆中，如果圆心角相等，那么它们所对弧相等，所对的弦相等”中，可否把条件“在同圆或等圆中”去掉？为什么？
在同一个圆中，如果弧相等，那么它们所对的圆心角相等，所对的弦相等．
弧、弦与圆心角关系定理的推论
在同一个圆中，如果弦相等，那么它们所对的圆心角相等，所对的弧相等．
如图，在等圆中，如果圆心角∠AOB ＝∠CO′D，你发现的等量关系是否依然成立？
通过平移和旋转将两个等圆变成同一个圆，我们发现：如果∠AOB =∠CO′D，那么 ，弦 AB = 弦 CD.
温馨提示：一条弦对应两条弧，由弦相等得到弧相等时需要区分优弧和劣弧.
(3) 圆心角相等，所对的弦相等. （ ）
(2) 等弧所对的弦相等. （ ）
(1) 等弦所对的弧相等. （ ）
∴∠BOC =∠COD =∠DOE = 35°.
∴∠AOE = 180° - 3×35° = 75°.
∴ AB = AC，△ABC 是等腰三角形.
又∵∠ACB = 60°，
∴△ABC 是等边三角形，AB = BC = CA.
∴∠AOB =∠BOC =∠AOC.
方法总结：弧、圆心角、弦之间等量关系的灵活转化是解决圆相关问题的重要法宝.
填一填： 如图，AB、CD 是⊙O 的两条弦．(1) 如果 AB = CD，那么_________，______________．(2) 如果 ，那么_________，_____________．(3) 如果∠AOB = ∠COD，那么__________，_________．
∠AOB = ∠COD
(4) 如果 AB = CD，OE⊥AB 于 E，OF⊥CD 于 F，OE 与 OF 相等吗？为什么？
∵△OAB 和△OCD 均为等腰三角形
OE⊥AB，OF⊥CD，
∴ AE = AB，CF = CD.
又∵ AB = CD，
又∵ OA = OC，
∴ Rt△AOE≌Rt△COF(H.L.)