华师大版九年级下册2. 二次函数y=ax2+bx+c的图象与性质课文内容课件ppt

这是一份华师大版九年级下册2. 二次函数y=ax2+bx+c的图象与性质课文内容课件ppt，共28页。PPT课件主要包含了导入新课，复习引入，做一做，合作探究，最小值，最大值，探究归纳，典例精析，方法归纳，矩形面积长×宽等内容，欢迎下载使用。
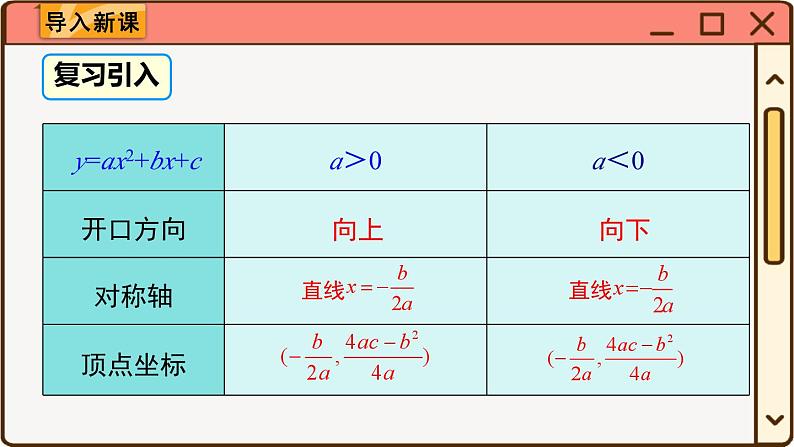
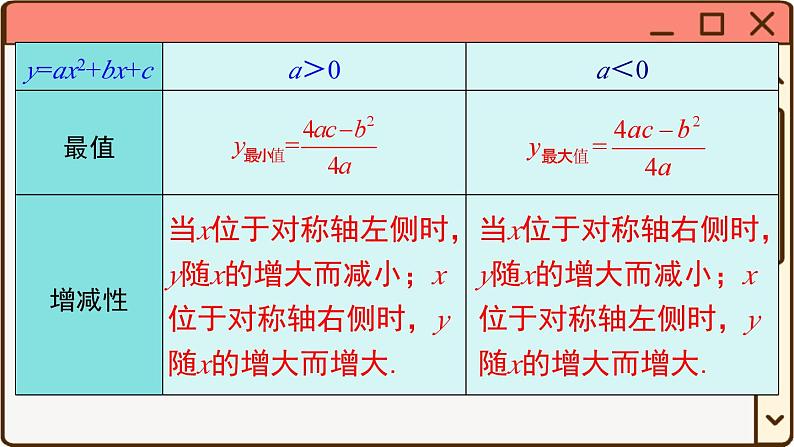
当x位于对称轴左侧时，y随x的增大而减小；x位于对称轴右侧时，y随x的增大而增大.
当x位于对称轴右侧时，y随x的增大而减小；x位于对称轴左侧时，y随x的增大而增大.
写出下列抛物线的开口方向、对称轴和顶点坐标.（1）y = x2 - 4x - 5; (2) y = -x2 - 3x + 4.
解：(1) 开口方向：向上；对称轴：x = 2； 顶点坐标：(2，-9).
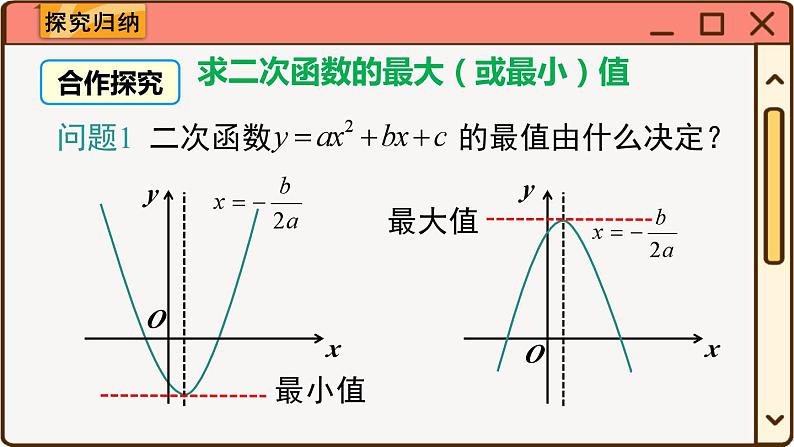
求二次函数的最大（或最小）值
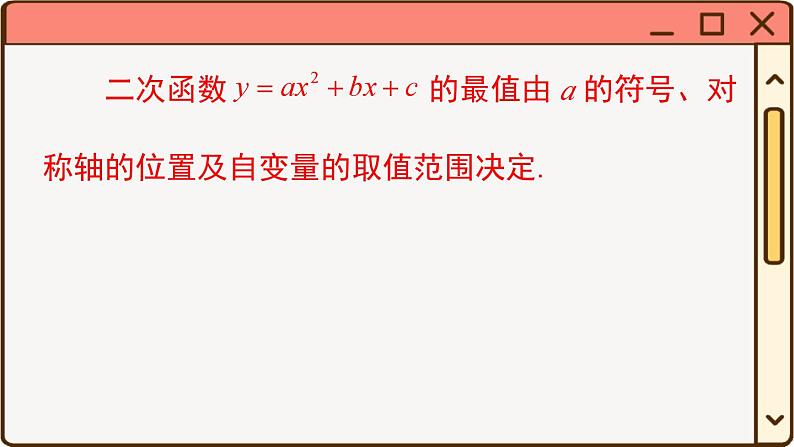
问题2 当自变量 x 为全体实数时，二次函数 y = ax2 + bx + c 的最值是多少？
问题3 当自变量 x 限定范围时，二次函数 y = ax2 + bx + c 的最值如何确定？
先判断 是否在限定范围内，若在，则二次函数在 x = 时取得一个最值，另一个最值需考察限定范围的端点处来决定；若不在，则根据二次函数的增减性确定其最值.
例1 求下列函数的最大值与最小值：
∴ 当 -3≤x≤1 时 y 随着 x 的增大而减小.
1. 配方，求二次函数的顶点坐标及对称轴；
2. 画出函数图象，标明对称轴，并在横坐标上标明 x 的取值范围；
3. 判断，判断 x 的取值范围与对称轴的位置关系，根据二次函数的性质及图象，确定当 x 取何值时函数有最大或最小值，然后根据 x 的值，求出函数的最值.
例2 用总长为 60 m 的篱笆围成矩形场地，矩形面积 S (m2) 随矩形一边长 l (m) 的变化而变化. 当 l 是多少米时，场地的面积 S 最大？
问题1 矩形面积公式是什么？
问题2 如何用 l 表示另一边？
问题3 面积 S 的函数关系式是什么？
另一边长为 (30 − l ) m
S = (30−l)l = −l 2+30l
问题4 当 l 是多少米时，场地的面积 S 最大？
S = l (30 - l)
= -l2 + 30l (0＜l＜30)，
也就是说，当 l 是 15 m 时，场地的面积 S 最大.
变式1 如图，用一段长为 60 m 的篱笆围成一个一边靠墙的矩形菜园，墙长 32 m，这个矩形的长、宽各为多少时，菜园的面积最大，最大面积是多少？
问题2 我们可以设面积为 S，如何设自变量？
问题1 变式 1 与例 2 有什么不同？
设垂直于墙的一边长为 x 米
篱笆长不等于周长 (少了一边)
问题4 如何求自变量 x 的取值范围？墙长 32 m 对此题有什么作用？
问题5 如何求面积 S 的最大值？
即当 x = 15 m 时，有 S最大值 = 450 m2.
0＜60－2x≤32，即 14≤x＜30.
问题3 面积 S 的函数关系式是什么？
S＝x(60－2x)＝－2x2＋60x＝－2(x－15)2＋450.
变式2 如图，用一段长为 60 m 的篱笆围成一个一边靠墙的矩形菜园，墙长 18 m，这个矩形的长、宽各为多少时，菜园的面积最大？最大面积是多少？
问题1 变式 2 与变式 1 有什么异同？
问题2 可否模仿变式 1 设未知数、列函数关系式？
问题3 可否试设与墙平行的一边长为 x 米？则如何表示另一边长与面积？
答案：设矩形面积为 S m2，与墙平行的一边为 x 米，则
问题4 当 x = 30 时 S 取最大值吗？为什么？
问题5 如何求自变量的取值范围？
问题6 如何求面积最大值？
由于 30 ＞18，因此只能利用函数的增减性求其最值.当 x = 18 m 时，S 有最大值是 378 m2.
不是，未考虑 x 的实际范围.
例3 用长为 6 米的铝合金材料做一个形状如图所示的矩形窗框. 窗框的高与宽各为多少时，它的透光面积最大？最大透光面积是多少？（铝合金型材宽度不计）
矩形窗框的透光面积 y 与 x 之间的函数关系式是
所以，当 x = 1 时，函数取得最大值，y最大值 = 1.5.
因此，所做矩形窗框的宽为 1 m、高为 1.5 m 时，它的透光面积最大，最大面积是 1.5 m2.
实际问题中求解二次函数最值问题，不一定都取图象顶点处，要根据自变量的取值范围确定. 通过变式 1 与变式 2 的对比，希望同学们能够理解函数图象的顶点、端点与最值的关系，以及何时取顶点处、何时取端点处才有符合实际意义的最值.
二次函数解决几何面积最值问题的方法
1. 求出函数解析式和自变量的取值范围；2. 当自变量的取值范围没有限制时，可直接利用公式 求它的最大值或最小值；3. 当自变量的取值范围有所限制时，可先配成顶点式， 然后画出函数图象的草图，再结合图象和自变量的 范围求函数最值.
1. 如图1，用长 8 m 的铝合金条制成如图的矩形窗框，那么最大的透光面积是 m2.
2.如图1，在△ABC 中， ∠B = 90°，AB = 12 cm，BC = 24 cm，动点 P 从点 A 开始沿 AB 向 B 以 2 cm/s 的速度移动(不与点 B 重合)，动点 Q 从点 B 开始沿 BC 以 4 cm/s 的速度移动(不与点 C 重合). 如果 P、Q 分别从 A、B 同时出发，那么经过 s，四边形 APQC 的面积最小.
3. 某广告公司设计一幅周长为 12 m 的矩形广告牌，广告设计费用每平方米 1000 元，设矩形的一边长为x(m),面积为 S (m2). (1) 写出 S 与 x 之间的关系式，并写出自变量 x 的取值范围；
解：(1) 因为矩形一边长为 x，则另一边长为(6 - x)，
∴ S = x(6 - x) = -x2 + 6x，其中 0＜x＜6.
解：S = -x2 + 6x = -(x - 3)2 + 9.
∴ 当 x = 3，即矩形的一边长为 3 m 时，矩形的面积最大，为 9 m2.
这时设计费最多，为 9×1000 = 9000 (元).
(2) 请你设计一个方案，使获得的设计费最多，并求出这个费用.