

2020-2021学年海南省澄迈县八年级下学期期末数学试题及答案
展开
这是一份2020-2021学年海南省澄迈县八年级下学期期末数学试题及答案,共17页。试卷主要包含了单选题,填空题,解答题等内容,欢迎下载使用。
1.化简(﹣)2的结果是( )
A.±3B.﹣3C.3D.9
2.下列计算正确的是( )
A.B.
C.D.
3.若二次根式在实数范围内有意义,则的取值范围是( )
A.B.C.D.
4.一次函数的图象不经过( )
A.第一象限B.第二象限C.第三象限D.第四象限
5.将直线向下平移个单位,得到直线( )
A.B.C.D.
6.下列条件中,不能判断一个三角形是直角三角形的是( )
A.三条边的比为2∶3∶4B.三条边满足关系a2=b2﹣c2
C.三条边的比为1∶1∶D.三个角满足关系∠B+∠C=∠A
7.小颖参加某公司应聘,成绩如下(每个方面满分20分)专业知识分,工作经验分,仪表形象分.若按图所显示的权重要求,则小颖的最后得分为( )
A.B.C.D.
8.如图,在□ABCD中,AB=4,BC=7,∠ABC的平分线交AD于点E,则ED等于( )
A.2B.3C.4D.5
9.如图,矩形ABCD的两条对角线交于点O,若∠AOD=120°,AB=6,则AC等于( )
A.8B.10C.12D.18
10.如图,四边形ABCD的每个顶点都在边长为1的正方形格点上,则边长为的线段是( )
A.ABB.BCC.CDD.AD
11.如图,在中,于要使得四边形是正方形,还需增加一个条件.在下列增加的条件中,不正确的是( )
A.B.C.D.
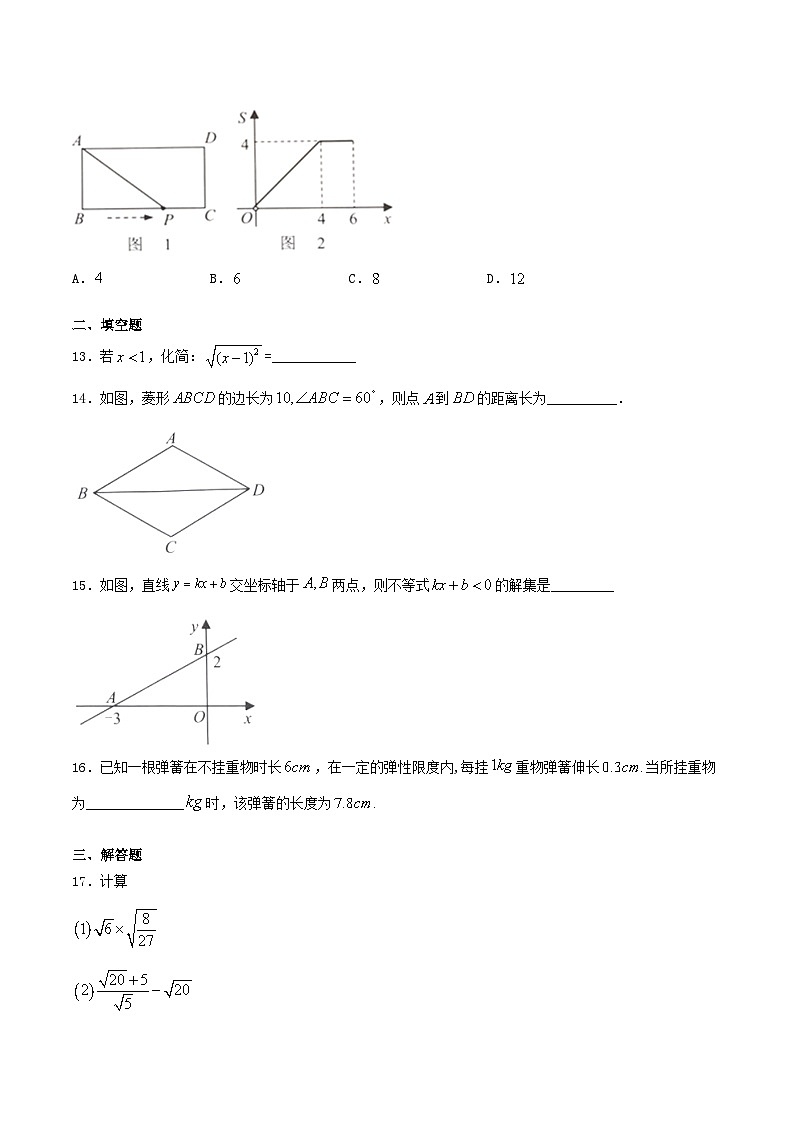
12.如图1,矩形中,,动点从点出发,沿路线作匀速运动,图2是的面积S与点P运动的路程x之间的函数图象,则该矩形的周长为( )
A.B.C.D.
二、填空题
13.若,化简:=____________
14.如图,菱形的边长为,则点到的距离长为__________.
15.如图,直线交坐标轴于两点,则不等式的解集是_________
16.已知一根弹簧在不挂重物时长,在一定的弹性限度内,每挂重物弹簧伸长当所挂重物为______________时,该弹簧的长度为
三、解答题
17.计算
18.木工师傅做一个人字形屋梁,如图所示,设计要求上弦,跨度为,现有一根木料打算做中柱(是的中线),判断长度为的木料能否做中柱,请通过计算说明.(注:设计只考虑长度、不计损耗)
19.甲、乙两人骑自行车匀速前往地,他们距地的路程与行驶时间之间的关系如图所示.请根据图象所提供的信息解答下列问题:
甲的速度是 ,乙的速度是
求出甲或乙距地的路程与行驶时间之间的函数关系式(任求一个);
直接写出在什么时间段内乙比甲离地更近?
20.甲、乙两工人同时加工同种圆柱形零件,质检部门在他们所加工的零件中各随机抽取个进行直径检测,测得数据(单位:)如下:
填写下表:
根据以上数据可以判断 工人生产的零件的质量比较稳定.
21.如图,在中,是边上的中线,是的中点,过点作,交的延长线于点,连结.
求证:
①
②四边形是平行四边形;
若,试判断四边形的形状,并证明你的结论.
22.如图,直线分别交x轴、y轴于A、B两点,直线BC与x轴交于点,P是线段AB上的一个动点点P与A、B不重合.
(1)求直线BC所对应的的函数表达式;
(2)设动点P的横坐标为t,的面积为S.
①求出S与t的函数关系式,并写出自变量t的取值范围;
②在线段BC上存在点Q,使得四边形COPQ是平行四边形,求此时点Q的坐标.
甲
乙
平均数
众数
中位数
方差
甲
乙
参考答案
1.C
【分析】
根据二次根式的性质即可求出答案.
【详解】
原式=3,
故选C.
【点睛】
本题考查二次根式的性质,解题的关键是熟练运用二次根式的性质,本题属于基础题型.
2.B
【解析】
解:A.不能合并.故选项错误;
B..故选项正确;
C..故选项错误;
D..故选项错误.
故选B.
3.D
【分析】
根据二次根式内为非负求解.
【详解】
要使二次根式有意义,则二次根式内非负
∴x-6≥0
解得:x≥6
故选:D.
【点睛】
本题考查二次根式有意义的条件,有意义的条件中,我们通常还需要注意,分式的分母不能为0.
4.A
【分析】
根据比例系数得到相应的象限,进而根据常数得到另一象限,判断即可;
【详解】
∵,
∴一次函数经过二四象限,
∵,
∴一次函数又经过第三象限,
∴一次函数的图象不经过第一象限.
故答案选A.
【点睛】
本题主要考查了一次函数的性质,准确理解是解题的关键.
5.D
【分析】
根据“上加下减”的口诀可得出结果.
【详解】
根据“上加下减”
∴将直线向下平移2个单位后变为:y=x+1-2
化简后为:y=x-1
故选:D.
【点睛】
本题考查平移,注意“左加右减”的口诀是针对x的,是对所有的x进行变形.
6.A
【分析】
根据直角三角形的判定方法,对选项进行一一分析,排除错误答案.
【详解】
A、三条边的比为2:3:4,22+32≠42,故不能判断一个三角形是直角三角形;
B、三条边满足关系a2=b2-c2,即a2+c2=b2,故能判断一个三角形是直角三角形;
C、三条边的比为1:1:,12+12=()2,故能判断一个三角形是直角三角形;
D、三个角满足关系∠B+∠C=∠A,则∠A为90°,故能判断一个三角形是直角三角形.
故选:A.
【点睛】
此题考查勾股定理的逆定理的应用.解题关键在于掌握判断三角形是否为直角三角形,已知三角形三边的长,只要利用勾股定理的逆定理加以判断即可;若已知角,只要求得一个角为90°即可.
7.C
【分析】
根据加权平均数公式计算即可求解.
【详解】
解:由题意得, .
故选:C
【点睛】
本题考查了求一组数据的加权平均数,如果一组数据的的权分别为,则加权平均数为.
8.B
【分析】
由平行四边形的性质可知AD∥BC,AD=BC,利用两直线平行得到一对内错角相等,由BE为角平分线得到一对角相等,等量代换得到∠ABE=∠AEB,利用等角对等边得到AB=AE=4,由AD-AE求出ED的长即可.
【详解】
解:∵四边形ABCD为平行四边形,
∴AD∥BC,AD=BC=7,
∴∠AEB=∠EBC,
∵BE平分∠ABC,
∴∠ABE=∠EBC,
∴∠AEB=∠ABE,
∴AB=AE=4,
∴ED=AD-AE=BC-AE=7-4=3.
故选:B.
【点睛】
此题考查了平行四边形的性质,角平分线的定义,以及等腰三角形的判定,熟练掌握平行四边形的性质是解本题的关键.
9.C
【分析】
根据矩形的对角线互相平分且相等可得OA=OB=AC,根据邻补角的定义求出∠AOB,然后判断出△AOB是等边三角形,根据等边三角形的性质可得OA=AB,然后求解即可.
【详解】
∵矩形ABCD的两条对角线交于点O,
∴OA=OB=AC,
∵∠AOD=120°,
∴∠AOB=180°-∠AOD=180°-120°=60°,
∴△AOB是等边三角形,
∴OA=AB=6,
∴AC=2OA=2×6=12.
故选C.
【点睛】
本题考查了矩形的性质,等边三角形的判定与性质,熟记矩形的对角线互相平分且相等是解题的关键.
10.A
【分析】
直接根据格点,运用勾股定理求解即可.
【详解】
由勾股定理得:AB==,AD==2,BC==5,CD==,
故选:A
【点睛】
此题主要考查正方形格点中勾股定理的运用,熟练掌握,即可解题.
11.C
【分析】
根据菱形的判定定理及正方形的判定定理即可解答;
【详解】
∵在平行四边形ABCD中,,
∴四边形ABCD是菱形,
当AC=BD时,菱形ABCD就是正方形,故A不符合题意;
当时,菱形ABCD就是正方形,故B不符合题意;
当AB=BC时,无法得到ABCD是正方形,故C符合题意;
当AO=BO时,则AO=BO=DO=CO,故菱形ABCD是正方形,故D不符合题意;
故答案选C.
【点睛】
本题主要考查了正方形的判定,准确利用平行四边形的性质是关键.
12.D
【分析】
由图象2看出当点P到达点C时,即x=4时,△ABP的面积最大,即△ABC的面积,可知BC的长,根据三角形面积公式可求出AB的长,即可求出矩形的周长.
【详解】
∵当点P到达点C时,△ABP的面积最大,即△ABC的面积,
∴由图象2可知BC=4,S△ABC=4,
∴S△ABC的面积=AB×BC=4,
∴AB=2,
∴该矩形的周长=2(AB+BC)=12,
故选:D.
【点睛】
本题主要考查了动点问题的函数图象.解题的关键是利用函数的图象读懂当即x=4时,△ABP的面积最大.
13.1-x
【详解】
解: ,
,
故答案为:1-x
14.
【分析】
作AO⊥BD于O,求出ABO=30°,根据直角三角形性质求出AO即可.
【详解】
解:作AO⊥BD于O,
∵四边形ABCD为菱形,
∴∠ABO=,
∴AO=.
即点到的距离长为5.
故答案为:5
【点睛】
本题考查了菱形的性质,含30°角的直角三角形性质,点到直线的距离定义,熟知相关概念和性质是解题关键.
15.
【分析】
直接读图,不等式小于0,在图上表示为函数在x轴下半部分的函数.
【详解】
∵求不等式的解集
由图形可知,当x<-3时,函数的图像在x轴下半部分
故答案为:x<-3.
【点睛】
本题考查一次函数与不等式的关系,需要注意求的不等式的不等号是“<”还是“≤”.
16.
【分析】
设弹簧长度为ycm,所挂重物为xkg,列出y与x的函数关系式,再把y=7.8代入函数关系式计算即可得解.
【详解】
设弹簧长度为ycm,所挂重物为xkg,
∵不挂重物时长6cm,在一定的弹性限度内,每挂1kg重物弹簧伸长0.3cm,
∴y=0.3x+6,
当y=7.8时,0.3x+6=7.8,
解得x=6,
即所挂重物为6kg.
故答案为:6.
【点睛】
本题考查一次函数的应用,弄清题意,正确写出函数关系式是解题的关键.
17.(1);(2)
【分析】
根据二次根式的性质和运算公式计算即可.
【详解】
原式
;
原式
.
【点睛】
本题考查了二次根式的混合运算,熟练掌握运算公式是解题的关键.
18.长度为的木料不能做中柱.
【分析】
由,AD是的中线,可得,在中,由勾股定理得:,由,可得结论.
【详解】
∵,AD是的中线,
,
在中,由勾股定理得:
,
,
长度为的木料不能做中柱.
【点睛】
本题主要考查了等腰三角形的性质,勾股定理,熟练掌握等腰三角形的性质是解题的关键.
19.(1)20,30;(2)或;(3)
【分析】
(1)由图中的时间和路程,可求出速度;
(2)点,在直线上,运用待定系数法即可解答;
(3)时二者相遇,由图可知,在小时这段时间内,乙比甲离A地更近;
【详解】
(1)从函数图像可知:甲用2.5小时行走了50km,乙用2小时行走了60km,
∴甲的速度是:;乙的速度是:;
故答案为:20;30;
(2)由函数图像知,甲函数过点,,设函数关系式为,
则有,
解得:,
∴所求函数关系式为;
同理即可得出乙距A地的路程Sy与行驶时间t之间的函数关系为:.
(3)从函数图象可知,在小时这段时间内,乙比甲离A地更近;
【点睛】
本题主要考查了一次函数的应用,准确计算是解题的关键.
20.(1)甲的众数为;乙的平均数为;乙的中位数为;(2)乙
【分析】
(1)利用平均数公式,求解乙的平均数;众数即为出现次数最多的数;中位数为最中间两组数据的平均数;
(2)比较方差,方差小的稳定情况.
【详解】
(1)甲的10组数据中,39.8出现的次数最多
∴甲的众数为;
乙的平均数=
∴乙的平均数为;
乙中,先将数据从小到大排列为:39.9、39.9、39.9、40、40、40、40、40、40.1、40.2
其中第5组数据为40,第6组数据为40
∴乙的中位数为
(2)∵甲大方差为0.03,乙的方差为0.008,其中0.008<0.03
∴乙比较稳定.
【点睛】
本题考查平均数、众数、中位数和方差,需要注意方差越小代表数据越稳定.
21.(1)①详见解析;②详见解析;(3)四边形是正方形,理由详见解析
【分析】
(1)①利用AF∥BC可得出,根据AD是BC的中线,可推导得出BD=CD,进而证全等;
②通过证AD∥CD且AF=CD可证平行四边形;
(2)通过证可得出正方形的结论.
【详解】
(1)是 边上的中线,
.
为的中点,
.
,
.
又
②,
,
四边形是平行四边形.
(2)四边形是正方形.
理由如下:
在中,是边上的中线,,
四边形是正方形.
【点睛】
本题考查平行四边形的证明,注意平行四边形,正方形的证明方法的不同和传承部分.
22.(1)y=2x+4;(2)①S=-2t+8(0<t<4);②点Q的坐标为(,).
【分析】
(1)根据函数表达式求出点B坐标,结合点C坐标求出BC的表达式;
(2)①根据三角形面积求法可得S与t的表达式;
②过点P作PQ∥x轴,交BC于点Q,得出P和Q的坐标,利用平行四边形的性质建立方程求解即可.
【详解】
解:(1)直线y=-x+4与x轴、y轴交点坐标分别为A(4,0)、B(0,4)两点.
设直线BC所对应的函数关系式为y=kx+4.
∵直线BC经过点C(-2,0),
∴-2k+4=0,解得:k=2,
∴直线BC所对应的函数关系式为y=2x+4.
(2)①由题意,设点P的坐标为(t,-t+4),
∴S=S△POA=×OA×yP=×4×(-t+4)=-2t+8.
即S=-2t+8(0<t<4).
②过点P作PQ∥x轴,交BC于点Q.
∵点P的坐标为(t,-t+4),
∴点Q的坐标为(,-t+4).
∵四边形COPQ是平行四边形,
∴PQ=OC,即.
解得:t=,
∴点Q的坐标为(,).
【点睛】
本题考查了一次函数的应用,求一次函数表达式,平行四边形的性质,解题的关键是画出图形,借助平行四边形的性质解题.
相关试卷
这是一份海南省澄迈县2022-2023学年七年级下学期期末考试数学试题,共5页。
这是一份海南省省直辖县级行政单位澄迈县2021-2022学年八年级下学期期末数学试题(word版含答案),共8页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
这是一份海南省省直辖县级行政单位澄迈县2021-2022学年七年级下学期期末数学试题(word版含答案),共7页。试卷主要包含了单选题,填空题,解答题等内容,欢迎下载使用。









