2024年中考数学专题训练 专题02 中线四大模型在三角形中的应用（专项训练）（原卷版+解析）

这是一份2024年中考数学专题训练 专题02 中线四大模型在三角形中的应用（专项训练）（原卷版+解析），共23页。

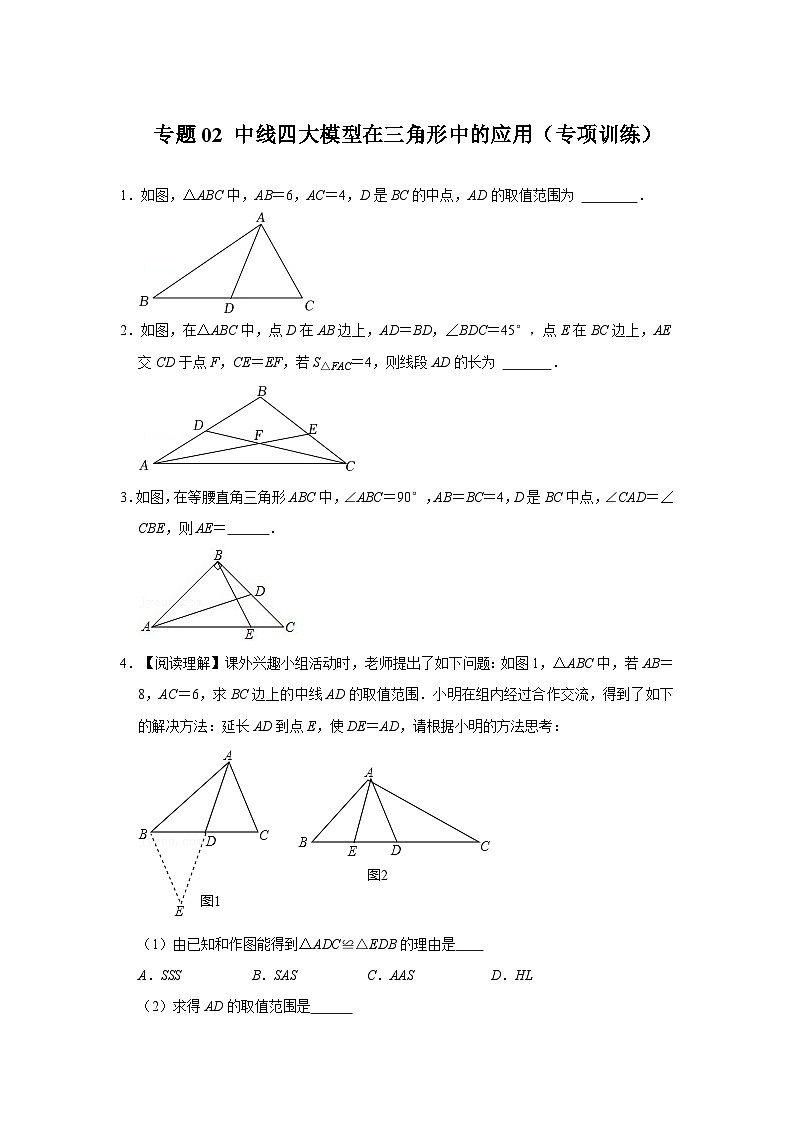
1．如图，△ABC中，AB＝6，AC＝4，D是BC的中点，AD的取值范围为 ．
2．如图，在△ABC中，点D在AB边上，AD＝BD，∠BDC＝45°，点E在BC边上，AE交CD于点F，CE＝EF，若S△FAC＝4，则线段AD的长为 ．
3．如图，在等腰直角三角形ABC中，∠ABC＝90°，AB＝BC＝4，D是BC中点，∠CAD＝∠CBE，则AE＝ ．
4．【阅读理解】课外兴趣小组活动时，老师提出了如下问题：如图1，△ABC中，若AB＝8，AC＝6，求BC边上的中线AD的取值范围．小明在组内经过合作交流，得到了如下的解决方法：延长AD到点E，使DE＝AD，请根据小明的方法思考：
（1）由已知和作图能得到△ADC≌△EDB的理由是
A．SSS B．SAS C．AAS D．HL
（2）求得AD的取值范围是
A．6＜AD＜8 B．6≤AD≤8 C．1＜AD＜7 D．1≤AD≤7
【方法感悟】
解题时，条件中若出现“中点”“中线”字样，可以考虑延长中线构造全等三角形，把分散的已知条件和所求证的结论集合到同一个三角形中．
【问题解决】
（3）如图2，已知：CD＝AB，∠BDA＝∠BAD，AE是△ABD的中线，求证：∠C＝∠BAE．
5．某校数学课外兴趣小组活动时，老师提出如下问题：
【探究】如图1，△ABC中，若AB＝8，AC＝6，点D是BC的中点，试探究BC边上的中线AD的取值范围．小明在组内经过合作交流，得到了如下的解决方法：延长AD到E，使DE＝AD，请补充完整证明“△ADC≌△EDB”的推理过程．
（1）求证：△ADC≌△EDB
证明：∵延长AD到点E，使DE＝AD
在△ADC和△EDB中AD＝ED（已作）∠ADC＝∠EDB（ ） CD＝BD（中点定义）
∴△ADC≌△EDB（ ）
（2）探究得出AD的取值范围是 ；
【感悟】解题时，条件中若出现“中点”“中线”等字样，可以考虑延长中线构造全等三角形，把分散的已知条件和所求证的结论集合到同一个三角形中．
【问题解决】
（3）如图2，AD是△ABC的中线，BE交AC于E，交AD于F，且AC＝BF．
求证：∠BFD＝∠CAD．
6．（1）如图1，AD是△ABC的中线，延长AD至点E，使ED＝AD，连接CE．
①证明△ABD≌△ECD；
②若AB＝5，AC＝3，设AD＝x，可得x的取值范围是 ；
（2）如图2，在△ABC中，D是BC边上的中点，DE⊥DF，DE交AB于点E，DF交AC于点F，连接EF，求证：BE+CF＞EF．
7．【教材呈现】如图是华师版八年级上册数学教材第69页的部分内容：
（1）【方法应用】如图①，在△ABC中，AB＝6，AC＝4，则BC边上的中线AD长度的取值范围是 ．
（2）【猜想证明】如图②，在四边形ABCD中，AB∥CD，点E是BC的中点，若AE是∠BAD的平分线，试猜想线段AB、AD、DC之间的数量关系，并证明你的猜想；
（3）【拓展延伸】如图③，已知AB∥CF，点E是BC的中点，点D在线段AE上，∠EDF＝∠BAE，若AB＝5，CF＝2，直接写出线段DF的长．
8．如图，已知AB＝12，AB⊥BC于B，AB⊥AD于A，AD＝5，BC＝10．点E是CD的中点，则AE的长是 ．
9．如图，已知AB＝12，AB⊥BC于B，AB⊥AD于A，AD＝5，BC＝10．点E是CD的中点，求AE的长．
10．如图，点D，E，F分别为△ABC三边的中点．若△ABC的周长为10，则△DEF的周长为 ．
如图，在四边形ABCD中，P是对角线BD的中点，E、F分别是AB、CD的中点，AD＝BC，∠FPE＝100°，则∠PFE的度数是 ．
11．如图，在△ABC中，∠ACB＝90°，AB＝10，BC＝6，M、N分别是AB、AC的中点，延长BC至点D，使CD＝BC，连结DM、DN、MN，求DN的长．
（1）求DN的长；
（2）直接写出△BDM的面积为 ．
12.【教材呈现】下面是华师版九年级上册数学教材第78页的部分内容．
请根据教材提示，结合图①，写出完整的证明过程．
【结论应用】如图②，在△ABC中，D、F分别是边BC、AB的中点，AD、CF相交于点G，GE∥AC交BC于点E，GH∥AB交BC于点H，则△EGH与△ABC的面积的比值为 ．
13．直角三角形两边的长为6和8，则该直角三角形斜边上的中线长为 ．
14．已知直角三角形斜边长为16，则这个直角三角形斜边上的中线长为 ．
15．如果一个直角三角形的两条直角边长分别为5cm、12cm，那么这个直角三角形斜边上的中线等于 cm．
例2：如图，在△ABC中，D、E分别是边BC、AB的中点，AD、CE相交于点G，求证：．
证明：连结ED．
专题02 中线四大模型在三角形中的应用（专项训练）
1．如图，△ABC中，AB＝6，AC＝4，D是BC的中点，AD的取值范围为 ．
【答案】 1＜AD＜5
【解答】解：延长AD到E，使DE＝AD，连接BE，
在△ACD与△EBD中，
，
∴△BDE≌△CDA（SAS），
∴BE＝AC，
∵AB＝6，AC＝4，
∴2＜AE＜10，
∴1＜AD＜5．
故答案为：1＜AD＜5．
2．如图，在△ABC中，点D在AB边上，AD＝BD，∠BDC＝45°，点E在BC边上，AE交CD于点F，CE＝EF，若S△FAC＝4，则线段AD的长为 ．
【答案】2
【解答】解：延长CD到点G，使DG＝CD，连接AG，过点H作AH⊥CG，垂足为H，
∵AD＝BD，∠BDC＝∠ADG，
∴△BDC≌△ADG（SAS），
∴∠G＝∠BCD，
∵EF＝EC，
∴∠BCD＝∠EFC，
∴∠G＝∠EFC，
∵∠EFC＝∠AFG，
∴∠G＝∠AFG，
∴AG＝AF，
∵AH⊥FG，
∴HG＝HF，
∴S△AHG＝S△AHF，
∵S△ADG＝S△BCD，S△BCD＝S△ADC，
∴S△ADG＝S△ADC，
∴S△AGH+S△ADH＝S△ADF+S△AFC，
∴S△AFH+S△ADH＝S△ADF+S△AFC，
∴S△ADH+S△ADF+S△ADH＝S△ADF+S△AFC，
∴2S△ADH＝S△AFC，
∵S△FAC＝4，
∴S△ADH＝2，
∵∠BDC＝45°，
∴∠BDC＝∠ADH＝45°，
∴AH＝DH，
∴AH•DH＝2，
∴AH＝2或AH＝﹣2（舍去），
∴AD＝AH＝2，
故答案为：2．
3．如图，在等腰直角三角形ABC中，∠ABC＝90°，AB＝BC＝4，D是BC中点，∠CAD＝∠CBE，则AE＝ ．
【答案】 3
【解答】解：过点B作BF∥AC，交AD的延长线于点F，
∴∠CBF＝∠C，∠DAC＝∠F，
∵∠ABC＝90°，AB＝BC＝4，
∴AC＝AB＝4，
∵D是BC中点，
∴BD＝CDBC＝2，
∴△ADC≌△FDB（AAS），
∴AC＝BF＝4，
∵∠CAD＝∠CBE，
∴∠CBE＝∠F，
∴△BCE∽△FBD，
∴＝，
∴＝，
∴CE＝，
∴AE＝AC﹣CE＝3，
故答案为：3．
4．【阅读理解】课外兴趣小组活动时，老师提出了如下问题：如图1，△ABC中，若AB＝8，AC＝6，求BC边上的中线AD的取值范围．小明在组内经过合作交流，得到了如下的解决方法：延长AD到点E，使DE＝AD，请根据小明的方法思考：
（1）由已知和作图能得到△ADC≌△EDB的理由是
A．SSS B．SAS C．AAS D．HL
（2）求得AD的取值范围是
A．6＜AD＜8 B．6≤AD≤8 C．1＜AD＜7 D．1≤AD≤7
【方法感悟】
解题时，条件中若出现“中点”“中线”字样，可以考虑延长中线构造全等三角形，把分散的已知条件和所求证的结论集合到同一个三角形中．
【问题解决】
（3）如图2，已知：CD＝AB，∠BDA＝∠BAD，AE是△ABD的中线，求证：∠C＝∠BAE．
【解答】（1）解：∵在△ADC和△EDB中，，
∴△ADC≌△EDB（SAS），
故答案为：B；
（2）解：∵由（1）知：△ADC≌△EDB，
∴BE＝AC＝6，AE＝2AD，
∵在△ABE中，AB＝8，由三角形三边关系定理得：8﹣6＜2AD＜8+6，
∴1＜AD＜7，
故答案为：C．
（3）证明：如图，延长AE到F，使EF＝AE，连接DF，
∵AE是△ABD的中线
∴BE＝ED，
在△ABE与△FDE中，，
∴△ABE≌△FDE（SAS），
∴AB＝DF，∠BAE＝∠EFD，
∵∠ADB是△ADC的外角，
∴∠DAC+∠ACD＝∠ADB＝∠BAD，
∴∠BAE+∠EAD＝∠BAD，∠BAE＝∠EFD，
∴∠EFD+∠EAD＝∠DAC+∠ACD，
∴∠ADF＝∠ADC，
∵AB＝DC，
∴DF＝DC，
在△ADF与△ADC中，，
∴△ADF≌△ADC（SAS）
∴∠C＝∠AFD＝∠BAE．
5．某校数学课外兴趣小组活动时，老师提出如下问题：
【探究】如图1，△ABC中，若AB＝8，AC＝6，点D是BC的中点，试探究BC边上的中线AD的取值范围．小明在组内经过合作交流，得到了如下的解决方法：延长AD到E，使DE＝AD，请补充完整证明“△ADC≌△EDB”的推理过程．
（1）求证：△ADC≌△EDB
证明：∵延长AD到点E，使DE＝AD
在△ADC和△EDB中AD＝ED（已作）∠ADC＝∠EDB（ ） CD＝BD（中点定义）
∴△ADC≌△EDB（ ）
（2）探究得出AD的取值范围是 ；
【感悟】解题时，条件中若出现“中点”“中线”等字样，可以考虑延长中线构造全等三角形，把分散的已知条件和所求证的结论集合到同一个三角形中．
【问题解决】
（3）如图2，AD是△ABC的中线，BE交AC于E，交AD于F，且AC＝BF．
求证：∠BFD＝∠CAD．
【解答】（1）证明：∵延长AD到点E，使DE＝AD，
在△ADC和△EDB中，
AD＝ED，∠ADC＝∠EDB（对顶角相等），CD＝BD（中点定义），
∴△ADC≌△EDB（SAS），
故答案为：对顶角相等；SAS；
（2）解：∵△ADC≌△EDB，
∴BE＝AC＝6，
∴AB﹣BE＜AE＜AB+BE，即1＜AD＜7，
故答案为：1＜AD＜7；
（3）证明：延长AD到H，使DH＝AD，
由（1）得，△ADC≌△HDB，
∴BH＝AC，∠BHD＝∠CAD，
∵AC＝BF，
∴BH＝BF，
∴∠BFD＝∠BHD，
∴∠BFD＝∠CAD．
6．（1）如图1，AD是△ABC的中线，延长AD至点E，使ED＝AD，连接CE．
①证明△ABD≌△ECD；
②若AB＝5，AC＝3，设AD＝x，可得x的取值范围是 ；
（2）如图2，在△ABC中，D是BC边上的中点，DE⊥DF，DE交AB于点E，DF交AC于点F，连接EF，求证：BE+CF＞EF．
【解答】（1）①证明：∵AD是△ABC的中线，
∴BD＝CD，
在△ADB和△ECD中，
，
∴△ABD≌△ECD（SAS）；
②解：由①知，△ABD≌△ECD，
∴CE＝AB，
∵AB＝5，
∴CE＝5，
∵ED＝AD，AD＝x，
∴AE＝2AD＝2x，
在△ACE中，AC＝3，
根据三角形的三边关系得，5﹣3＜2x＜5+3，
∴1＜x＜4，
故答案为：1＜x＜4；
（2）证明：如图2，延长FD，截取DH＝DF，连接BH，EH，
∵DH＝DF，DE⊥DF，
即∠EDF＝∠EDH＝90°，DE＝DE，
∴△DEF≌△DEH（SAS），
∴EH＝EF，
∵AD是中线，
∴BD＝CD，
∵DH＝DF，∠BDH＝∠CDF，
∴△BDH≌△CDF（SAS），
∴CF＝BH，
∵BE+BH＞EH，
∴BE+CF＞EF．
7．【教材呈现】如图是华师版八年级上册数学教材第69页的部分内容：
（1）【方法应用】如图①，在△ABC中，AB＝6，AC＝4，则BC边上的中线AD长度的取值范围是 ．
（2）【猜想证明】如图②，在四边形ABCD中，AB∥CD，点E是BC的中点，若AE是∠BAD的平分线，试猜想线段AB、AD、DC之间的数量关系，并证明你的猜想；
（3）【拓展延伸】如图③，已知AB∥CF，点E是BC的中点，点D在线段AE上，∠EDF＝∠BAE，若AB＝5，CF＝2，直接写出线段DF的长．
【解答】解：（1）延长AD到E，使AD＝DE，连接BE，
∵AD是BC边上的中线，
∴BD＝CD，
在△ADC和△EDB中，
，
∴△ADC≌△EDB（SAS），
∴AC＝BE＝4，
在△ABE中，AB﹣BE＜AE＜AB+BE，
∴6﹣4＜2AD＜6+4，
∴1＜AD＜5，
故答案为：1＜AD＜5．
（2）结论：AD＝AB+DC．
理由：如图②中，延长AE，DC交于点F，
∵AB∥CD，
∴∠BAF＝∠F，
在△ABE和△FCE中，
，
∴△ABE≌△FEC（AAS），
∴CF＝AB，
∵AE是∠BAD的平分线，
∴∠BAF＝∠FAD，
∴∠FAD＝∠F，
∴AD＝DF，
∵DC+CF＝DF，
∴DC+AB＝AD．
（3）如图③，延长AE交CF的延长线于点G，
∵E是BC的中点，
∴CE＝BE，
∵AB∥CF，
∴∠BAE＝∠G，
在△AEB和△GEC中，
，
∴△AEB≌△GEC（AAS），
∴AB＝GC，
∵∠EDF＝∠BAE，
∴∠FDG＝∠G，
∴FD＝FG，
∴AB＝DF+CF，
∵AB＝5，CF＝2，
∴DF＝AB﹣CF＝3．
8．如图，已知AB＝12，AB⊥BC于B，AB⊥AD于A，AD＝5，BC＝10．点E是CD的中点，则AE的长是 ．
【解答】方法一：
解：连接DB，延长DA到F，使AD＝AF．连接FC，
∵AD＝5，
∴AF＝5，
又∵点E是CD的中点，
∴EA为△DFC的中位线，则AE＝CF，
在Rt△ABD中，
AD2+AB2＝DB2，
∴BD＝＝13，
∵AB⊥BC，AB⊥AD，
∴AD∥BC，
又∵DF＝BC，
∴四边形DBCF是平行四边形，
∴FC＝DB＝13，
∴AE＝．
故答案为：．
方法二：
连接BE并延长，延长DA交BE延长线于点F，
∵AB⊥BC，AB⊥AD，
∴AD∥BC，
∴∠D＝∠C，
在△DEF和△CEB中，
，
∴△DEF≌△CEB（ASA），
∴DF＝BC＝10，BE＝FE，
∵DA＝5，
∴AF＝5，
在Rt△ABF中，
AF2+AB2＝FB2，
∴BF＝＝13，
∴AE＝BF＝．
故答案为：．
9．如图，已知AB＝12，AB⊥BC于B，AB⊥AD于A，AD＝5，BC＝10．点E是CD的中点，求AE的长．
【解答】解：如图，延长AE交BC于F．
∵AB⊥BC，AB⊥AD，
∴AD∥BC
∴∠D＝∠C，∠DAE＝∠CFE，
又∵点E是CD的中点，
∴DE＝CE．
∵在△AED与△FEC中，
，
∴△AED≌△FEC（AAS），
∴AE＝FE，AD＝FC．
∵AD＝5，BC＝10．
∴BF＝5
在Rt△ABF中，，
∴AE＝AF＝6.5．
10．如图，点D，E，F分别为△ABC三边的中点．若△ABC的周长为10，则△DEF的周长为 ．
【答案】5
【解答】解：∵D、E、F分别是AB、AC、BC的中点，
∴FD、FE、DE为△ABC中位线，
∴DF＝AC，FE＝AB，DE＝BC；
∴DF+FE+DE＝AC+AB+BC＝（AB+AC+CB）＝×10＝5，
故答案为：5．
如图，在四边形ABCD中，P是对角线BD的中点，E、F分别是AB、CD的中点，AD＝BC，∠FPE＝100°，则∠PFE的度数是 ．
【解答】解：∵P是对角线BD的中点，E是AB的中点，
∴EP＝AD，
同理，FP＝BC，
∵AD＝BC，
∴PE＝PF，
∵∠FPE＝100°，
∴∠PFE＝40°，
故答案为：40°．
11．如图，在△ABC中，∠ACB＝90°，AB＝10，BC＝6，M、N分别是AB、AC的中点，延长BC至点D，使CD＝BC，连结DM、DN、MN，求DN的长．
（1）求DN的长；
（2）直接写出△BDM的面积为 ．
【考点】三角形中位线定理；勾股定理．
【专题】等腰三角形与直角三角形；运算能力．
【解答】解：（1）连接CM，
在Rt△ACB中，∠ACB＝90°，M是AB的中点，
∴CM＝AB＝5，
∵M，N分别是AB、AC的中点，BC＝6，
∴MN∥BC，MN＝BC＝3，
∵CD＝BC，
∴CD＝BC＝3，
∴CD＝MN，
∵MN∥BC，
∴四边形NDCM为平行四边形，
∴DN＝CM＝5；
（2）由（1）知，CD＝3，则BD＝CD+BC＝3+6＝9．
在直角△ABC中，∠ACB＝90°，AB＝10，BC＝6，则AC＝＝＝8．
∵N是AC的中点，
∴NC＝AC＝4．
∴S△BDM＝BD•CN＝×9×4＝18．
故答案为：18．
12.【教材呈现】下面是华师版九年级上册数学教材第78页的部分内容．
请根据教材提示，结合图①，写出完整的证明过程．
【结论应用】如图②，在△ABC中，D、F分别是边BC、AB的中点，AD、CF相交于点G，GE∥AC交BC于点E，GH∥AB交BC于点H，则△EGH与△ABC的面积的比值为 ．
【解答】解：【教材呈现】连接DE，如图①，
∵D、E分别为BC、BA的中点，
∴DE为△ABC的中位线，
∴DE∥AC，DE＝AC，
∴△DEG∽△ACG，
∴，
∴，
即；
【结论应用】∵D、F分别是边BC、AB的中点，
∴，BD＝CD，
∵GE∥AC，
∴△DEG∽△DCA，
∴，
∴，
同理可得，，
∴．
故答案为：
13．直角三角形两边的长为6和8，则该直角三角形斜边上的中线长为 ．
【解答】解：①当6和8均为直角边时，斜边＝10，
则斜边上的中线＝5；
②当6为直角边，8为斜边时，
则斜边上的中线＝4．
故斜边上的中线长为：4或5．
故答案为：4或5．
14．已知直角三角形斜边长为16，则这个直角三角形斜边上的中线长为 ．
【解答】解：
∵在△ACB中，∠ACB＝90°，CD是斜边AB上的中线，AB＝16，
∴CD＝AB＝8，
故答案为：8．
15．如果一个直角三角形的两条直角边长分别为5cm、12cm，那么这个直角三角形斜边上的中线等于 cm．
【解答】解：如图，在△ABC中，∠C＝90°，AC＝12cm，BC＝5cm，CD为斜边AB上的中线，
则根据勾股定理知，AB＝＝13cm，
CD＝AB＝cm；
故答案是：．
例2：如图，在△ABC中，D、E分别是边BC、AB的中点，AD、CE相交于点G，求证：．
证明：连结ED．