

2024年中考数学专题训练 专题06 半角模型综合应用(知识解读)
展开角含半角模型,顾名思义即一个角包含着它的一半大小的角。它主要包含:等腰直角三角形角含半角模型;正方形中角含半角模型两种类型。解决类似问题的常见办法主要有两种:旋转目标三角形法和翻折目标三角形法。
【方法技巧】
类型一:等腰直角三角形角含半角模型
(1)如图,在△ABC中,AB=AC,∠BAC=90°,点D,E在BC上,且∠DAE=45°,则:BD+CE=DE.
旋转法 翻折法
作法1:将△ABD旋转90° 作法2:分别翻折△ABD,△ACE
(2)如图,在△ABC中,AB=AC,∠BAC=90°,点D在BC上,点E在BC延长线上,且∠DAE=45°,则:BD+CE=DE.
(3)如图,将等腰直角三角形变成任意等腰三角形时,亦可以进行两种方法的操作处理..
任意等腰三角形
类型二:正方形中角含半角模型
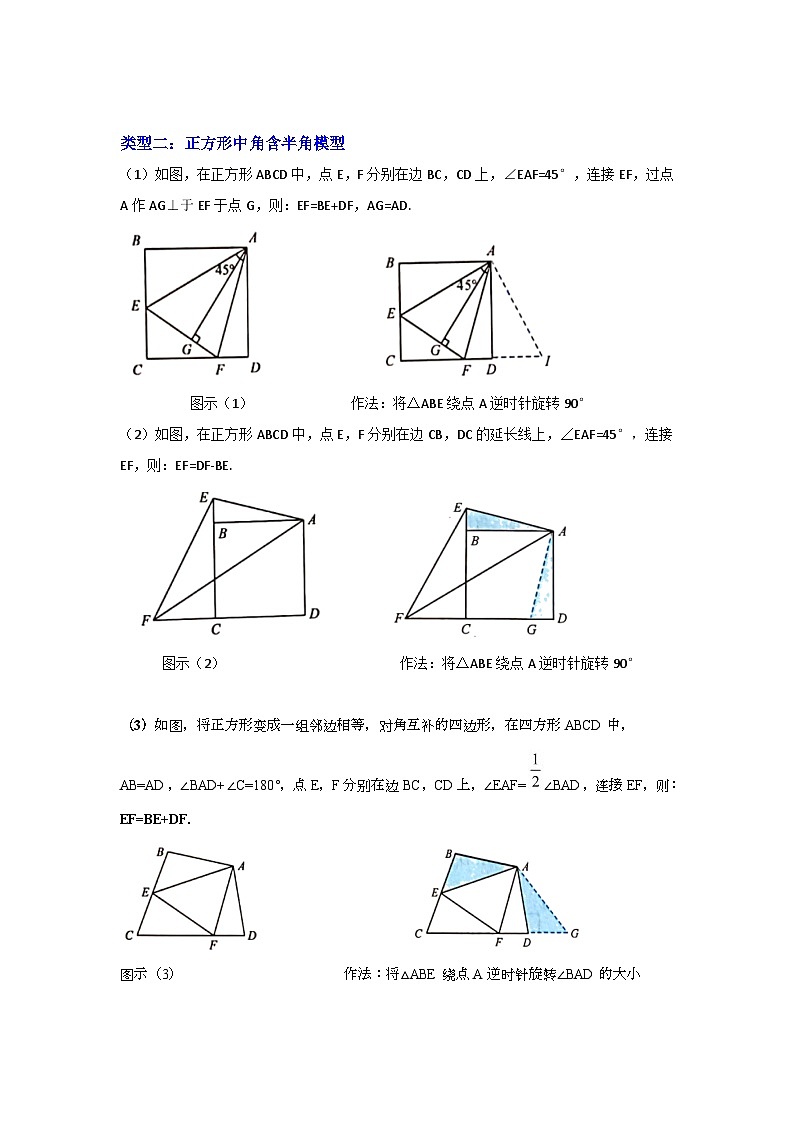
(1)如图,在正方形ABCD中,点E,F分别在边BC,CD上,∠EAF=45°,连接EF,过点A作AG⊥于EF于点G,则:EF=BE+DF,AG=AD.
图示(1) 作法:将△ABE绕点A逆时针旋转90°
(2)如图,在正方形ABCD中,点E,F分别在边CB,DC的延长线上,∠EAF=45°,连接EF,则:EF=DF-BE.
图示(2) 作法:将△ABE绕点A逆时针旋转90°
(3)如图,将正方形变成一组邻边相等,对角互补的四边形,在四方形ABCD中,AB=AD,∠BAD+∠C=180°,点E,F分别在边BC,CD上,∠EAF=∠BAD,连接EF,则:EF=BE+DF.
图示(3) 作法:将△ABE绕点A逆时针旋转∠BAD的大小
类型三:等边三角形中120°含60°的半角模型
作辅助线:延长FC到G,使得CG=BE,连接DG
结论:▲DEF≌▲DGF;EF=BE+CF
【典例分析】
【类型一:等腰直角三角形角含半角模型】
【典例1】如图,四边形ABCD中,∠A=∠BCD=90°,BC=CD,若将△ABC绕着点C逆时针旋转90°得△EDC.
(1)求证:∠ADC+∠CDE=180°;
(2)若AB=3cm,AC=,求AD的长;
(3)在(2)的条件下,求四边形ABCD的周长和面积.
【变式1-1】如图,Rt△ABC中,∠BAC=90°,AB=AC,D、E为BC边上两点,∠DAE=45°,过A点作AF⊥AE,且AF=AE,连接DF、BF.下列结论:①△ABF≌△ACE,②AD平分∠EDF;③若BD=4,CE=3,则AB=6;④若AB=BE,S△ABD=,其中正确的个数有( )
A.1个B.2个C.3个D.4个
【变式1-2】如图,等腰直角三角形ABC中,∠BAC=90°,AB=AC,点M,N在边BC上,且∠MAN=45°.若BM=1,CN=3,则MN的长为 .
【类型二:正方形中角含半角模型】
【典例2】(2022春•西山区校级月考)如图,已知正方形ABCD,点E、F分别是AB、BC边上,且∠EDF=45°,将△DAE绕点D逆时针旋转90°,得到△DCM.
(1)求证:△EDF≌△MDF;
(2)若正方形ABCD的边长为5,AE=2时,求EF的长?
【变式2-1】(2022春•路北区期末)如图,在边长为6的正方形ABCD内作∠EAF=45°,AE交BC于点E,AF交CD于点F,连接EF,将△ADF绕点A顺时针旋转90°得到△ABG.
(1)求证:GE=FE;
(2)若DF=3,求BE的长为 .
【变式2-2】(2021秋•山西期末)阅读以下材料,并按要求完成相应的任务:
任务:
如图3,在四边形ABCD中,AB=AD,∠B=∠D=90°,∠BAD=120°,以A为顶点的∠EAF=60°,AE、AF与BC、CD边分别交于E、F两点.请参照阅读材料中的解题方法,你认为结论EF=BE+DF是否依然成立,若成立,请写出证明过程;若不成立,请说明理由.
【典例3】已知正方形ABCD中,∠MAN=45°,∠MAN绕点A顺时针旋转,它的两边分别交CB,DC(或它们的延长线)于点M,N,AH⊥MN于点H.
(1)如图①,当∠MAN绕点A旋转到BM=DN时,请你直接写出AH与AB的数量关系: ;
(2)如图②,当∠MAN绕点A旋转到BM≠DN时,(1)中发现的AH与AB的数量关系还成立吗?如果不成立请写出理由,如果成立请证明;
(3)如图③,已知∠MAN=45°,AH⊥MN于点H,且MH=2,AH=6,求NH的长.(可利用(2)得到的结论)
【变式3-1】探究:
(1)如图1,在正方形ABCD中,E、F分别是BC、CD上的点,且∠EAF=45°,试判断BE、DF与EF三条线段之间的数量关系,直接写出判断结果: ;
(2)如图2,若把(1)问中的条件变为“在四边形ABCD中,AB=AD,∠B+∠D=180°,E、F分别是边BC、CD上的点,且∠EAF=∠BAD”,则(1)问中的结论是否仍然成立?若成立,请给出证明,若不成立,请说明理由;
(3)在(2)问中,若将△AEF绕点A逆时针旋转,当点分别E、F运动到BC、CD延长线上时,如图3所示,其它条件不变,则(1)问中的结论是否发生变化?若变化,请给出结论并予以证明.
【变式3-2】已知:如图边长为2的正方形ABCD中,∠MAN的两边分别交BC、CD边于M、N两点,且∠MAN=45°
①求证:MN=BM+DN;
②若AM、AN交对角线BD于E、F两点.设BF=y,DE=x,求y与x的函数关系式.
【类型三:等边三角形中120°含60°的半角模型】
【典例4】已知在△ABC中,AB=AC,D,E是BC边上的点,将△ABD绕点A旋转,得到△ACD',连接D'E.
(Ⅰ)如图1,当∠BAC=120°,∠DAE=60°时,求证:DE=D'E;
(Ⅱ)如图2,当DE=D'E时,请写出∠DAE与∠BAC的数量关系,并说明理由.
(Ⅲ)当∠BAC=90°,DE=D'E,EC=CD'时,请直接写出BD与DE的数量关系(不必说明理由).
【变式4-1】(2017秋•锦江区期末)在△ABC中,AB=AC,点E,F是边BC所在直线上与点B,C不重合的两点.
(1)如图1,当∠BAC=90°,∠EAF=45°时,直接写出线段BE,CF,EF的数量关系;(不必证明)
(2)如图2,当∠BAC=60°,∠EAF=30°时,已知BE=3,CF=5,求线段EF的长度;
(3)如图3,当∠BAC=90°,∠EAF=135°时,请探究线段CE,BF,EF的数量关系,并证明.
【变式4-2】等边△ABC,D为△ABC外一点,∠BDC=120°,BD=DC,∠MDN=60°,射线DM与直线AB相交于点M,射线DN与直线AC相交于点N,
①当点M、N在边AB、AC上,且DM=DN时,直接写出BM、NC、MN之间的数量关系.
②当点M、N在边AB、AC上,且DM≠DN时,猜想①中的结论还成立吗?若成立,请证明.
③当点M、N在边AB、CA的延长线上时,请画出图形,并写出BM、NC、MN之间的数量关系.
专题06 半角模型(知识解读)
【专题说明】
角含半角模型,顾名思义即一个角包含着它的一半大小的角。它主要包含:等腰直角三角形角含半角模型;正方形中角含半角模型两种类型。解决类似问题的常见办法主要有两种:旋转目标三角形法和翻折目标三角形法。
【方法技巧】
类型一:等腰直角三角形角含半角模型
(1)如图,在△ABC中,AB=AC,∠BAC=90°,点D,E在BC上,且∠DAE=45°,则:BD+CE=DE.
旋转法 翻折法
作法1:将△ABD旋转90° 作法2:分别翻折△ABD,△ACE
(2)如图,在△ABC中,AB=AC,∠BAC=90°,点D在BC上,点E在BC延长线上,且∠DAE=45°,则:BD+CE=DE.
(3)如图,将等腰直角三角形变成任意等腰三角形时,亦可以进行两种方法的操作处理..
任意等腰三角形
类型二:正方形中角含半角模型
(1)如图,在正方形ABCD中,点E,F分别在边BC,CD上,∠EAF=45°,连接EF,过点A作AG⊥于EF于点G,则:EF=BE+DF,AG=AD.
图示(1) 作法:将△ABE绕点A逆时针旋转90°
(2)如图,在正方形ABCD中,点E,F分别在边CB,DC的延长线上,∠EAF=45°,连接EF,则:EF=DF-BE.
图示(2) 作法:将△ABE绕点A逆时针旋转90°
(3)如图,将正方形变成一组邻边相等,对角互补的四边形,在四方形ABCD中,AB=AD,∠BAD+∠C=180°,点E,F分别在边BC,CD上,∠EAF=∠BAD,连接EF,则:EF=BE+DF.
图示(3) 作法:将△ABE绕点A逆时针旋转∠BAD的大小
类型三:等边三角形中120°含60°的半角模型
作辅助线:延长FC到G,使得CG=BE,连接DG
结论:▲DEF≌▲DGF;EF=BE+CF
【典例分析】
【类型一:等腰直角三角形角含半角模型】
【典例1】如图,四边形ABCD中,∠A=∠BCD=90°,BC=CD,若将△ABC绕着点C逆时针旋转90°得△EDC.
(1)求证:∠ADC+∠CDE=180°;
(2)若AB=3cm,AC=,求AD的长;
(3)在(2)的条件下,求四边形ABCD的周长和面积.
【解答】(1)证明:如图,在四边形ABCD中,∠A=∠BCD=90°,则∠B+∠ADC=180°.
∵将△ABC绕着点C逆时针旋转90°得△EDC,
∴△ABC≌△EDC,
∴∠CDE=∠CBA,
∴∠ADC+∠CDE=180°;
(2)解:∵将△ABC绕着点C逆时针旋转90°得△EDC,
∴AC=EC=,AB=ED=3cm,∠ACE=90°,
∴AE=AC=8cm,
∴AD=AE﹣EC=AE﹣AB=5cm;
(3)解:如图,连接BD.
由(2)知,AD=5cm.
则在直角△ABD中,由勾股定理得到:BD==.
又∵BC=CD,∠BCD=90°,
∴BC=CD==,
∴四边形ABCD的周长为:AB+AD+2BC=3+5+2=8+2;
∵△ABC≌△EDC,
∴四边形ABCD的面积=△ACE的面积=AC•CE=×4×4=16(cm2).
综上所述,四边形ABCD的周长为(8+2)cm,面积为16cm2.
【变式1-1】如图,Rt△ABC中,∠BAC=90°,AB=AC,D、E为BC边上两点,∠DAE=45°,过A点作AF⊥AE,且AF=AE,连接DF、BF.下列结论:①△ABF≌△ACE,②AD平分∠EDF;③若BD=4,CE=3,则AB=6;④若AB=BE,S△ABD=,其中正确的个数有( )
A.1个B.2个C.3个D.4个
【答案】C
【解答】解:∵AF⊥AE,
∴∠FAE=90°,
∵∠BAC=90°,
∴∠FAE﹣∠BAE=∠BAC﹣∠BAE,
∴∠FAB=∠EAC,
∵AB=AC,AF=AE,
∴△ABF≌△ACE(SAS),
故①正确;
∵∠DAE=45°,∠FAE=90°,
∴∠FAD=∠FAE﹣∠DAE=45°,
∴∠FAD=∠DAE,
∵AD=AD,AF=AE,
∴△FAD≌△EAD(SAS),
∴∠FDA=∠EDA,
∴AD平分∠EDF,
故②正确;
在Rt△ABC中,∠BAC=90°,AB=AC,
∴∠ABC=∠C=45°,BC=AB,
∵△ABF≌△ACE,
∴∠ABF=∠C=45°,BF=CE=3,
∴∠FBD=∠ABF+∠ABD=90°,
∴DF===5,
∵△FAD≌△EAD,
∴FD=ED=5,
∴BC=BD+DE+CE=4+5+3=12,
∴AB=6,
故③正确;
∵AB=BE,∠ABE=45°,
∴∠BAE=∠BEA=67.5°,
∵∠DAE=45°,
∴∠ADE=180°﹣∠DAE﹣∠AED=67.5°,
∴∠ADB=∠AEC,
∵AB=AC,∠ABE=∠C=45°,
∴△ABD≌△ACE(AAS),
∴BD=CE,
∵BF=CE,
∴BD=BF,
∵∠FBD=90°,
∴DF=BD,
∴DE=BD,
∴S△ADE=S△ABD,
故④错误;
综上所述,正确的个数有3个,
故选:C
【变式1-2】如图,等腰直角三角形ABC中,∠BAC=90°,AB=AC,点M,N在边BC上,且∠MAN=45°.若BM=1,CN=3,则MN的长为 .
【解答】解:将△AMB逆时针旋转90°到△ACF,连接NF,
∴CF=BM,AF=AM,∠B=∠ACF.∠2=∠3,
∵△ABC是等腰直角三角形,AB=AC,∠BAC=90°,
∴∠B=∠ACB=45°,
∵∠MAN=45°,
∴∠NAF=∠1+∠3=∠1+∠2=90°﹣45°=45°=∠NAF,
在△MAN和△FAN中
∴△MAN≌△FAN,
∴MN=NF,
∵∠ACF=∠B=45°,∠ACB=45°,
∴∠FCN=90°,
∵CF=BM=1,CN=3,
∴在Rt△CFN中,由勾股定理得:MN=NF==,
故答案为:.
【类型二:正方形中角含半角模型】
【典例2】(2022春•西山区校级月考)如图,已知正方形ABCD,点E、F分别是AB、BC边上,且∠EDF=45°,将△DAE绕点D逆时针旋转90°,得到△DCM.
(1)求证:△EDF≌△MDF;
(2)若正方形ABCD的边长为5,AE=2时,求EF的长?
【解答】(1)证明:∵四边形ABCD是正方形,
∴∠A=∠B=∠DCF=90°,AD=AB=BC=5,
由旋转得:
∠A=∠DCM=90°,DE=DM,∠EDM=90°,
∴∠DCF+∠DCM=180°,
∴F、C、M三点在同一条直线上,
∵∠EDF=45°,
∴∠FDM=∠EDM﹣∠EDC=45°,
∴∠EDF=FDM,
∵DF=DF,
∴△EDF≌△MDF(SAS);
(2)设CF=x,
∴BF=BC﹣CF=5﹣x,
由旋转得:AE=CM=2,
∴BE=AB﹣AE=3,FM=CF+CM=2+x,
∵△EDF≌△MDF,
∴EF=FM=2+x,
在Rt△EBF中,BE2+BF2=EF2,
∴9+(5﹣x)2=(2+x)2,
∴x=,
∴EF=2+x=,
∴EF的长为.
【变式2-1】(2022春•路北区期末)如图,在边长为6的正方形ABCD内作∠EAF=45°,AE交BC于点E,AF交CD于点F,连接EF,将△ADF绕点A顺时针旋转90°得到△ABG.
(1)求证:GE=FE;
(2)若DF=3,求BE的长为 .
【解答】(1)证明:∵将△ADF绕点A顺时针旋转90°得到△ABG,
∴△ADF≌△ABG,
∴DF=BG,∠DAF=∠BAG,
∵∠DAB=90°,∠EAF=45°,
∴∠DAF+∠EAB=45°,
∴∠BAG+∠EAB=45°,
∴∠EAF=∠EAG,
在△EAG和△EAF中,
,
∴△EAG≌△EAF(SAS),
∴GE=FE,
(2)解:设BE=x,则GE=BG+BE=3+x,CE=6﹣x,
∴EF=3+x,
∵CD=6,DF=3,
∴CF=3,
∵∠C=90°,
∴(6﹣x)2+32=(3+x)2,
解得,x=2,
即BE=2,
【变式2-2】(2021秋•山西期末)阅读以下材料,并按要求完成相应的任务:
任务:
如图3,在四边形ABCD中,AB=AD,∠B=∠D=90°,∠BAD=120°,以A为顶点的∠EAF=60°,AE、AF与BC、CD边分别交于E、F两点.请参照阅读材料中的解题方法,你认为结论EF=BE+DF是否依然成立,若成立,请写出证明过程;若不成立,请说明理由.
【解答】解:成立.
证明:将△ADF绕点A顺时针旋转120°得到△ABM,
∴△ABM≌△ADF,∠ABM=∠D=90°,∠MAB=∠FAD,AM=AF,MB=DF,
∴∠MBE=∠ABM+∠ABE=180°,
∴M、B、E三点共线,
∴∠MAE=∠MAB+∠BAE=∠FAD+∠BAE=∠BAD﹣∠EAF=60°,
∴∠MAE=∠FAE,
∵AE=AE,AM=AF,
∴△MAE≌△FAE(SAS),
∴ME=EF,
∴EF=ME=MB+BE=DF+BE.
【典例3】已知正方形ABCD中,∠MAN=45°,∠MAN绕点A顺时针旋转,它的两边分别交CB,DC(或它们的延长线)于点M,N,AH⊥MN于点H.
(1)如图①,当∠MAN绕点A旋转到BM=DN时,请你直接写出AH与AB的数量关系: ;
(2)如图②,当∠MAN绕点A旋转到BM≠DN时,(1)中发现的AH与AB的数量关系还成立吗?如果不成立请写出理由,如果成立请证明;
(3)如图③,已知∠MAN=45°,AH⊥MN于点H,且MH=2,AH=6,求NH的长.(可利用(2)得到的结论)
【解答】解:(1)∵正方形ABCD,
∴AB=AD,∠B=∠D=∠BAD=90°,
在Rt△ABM和Rt△ADN中,
,
∴Rt△ABM≌Rt△ADN(SAS),
∴∠BAM=∠DAN,AM=AN,
∵∠MAN=45°,
∴∠BAM+∠DAN=45°,
∴∠BAM=∠DAN=22.5°,
∵∠MAN=45°,AM=AN,AH⊥MN
∴∠MAH=∠NAH=22.5°,
∴∠BAM=∠MAH,
在Rt△ABM和Rt△AHM中,
,
∴Rt△ABM≌Rt△AHM(AAS),
∴AB=AH,
故答案为:AB=AH;
(2)AB=AH成立,理由如下:
延长CB至E,使BE=DN,如图:
∵四边形ABCD是正方形,
∴AB=AD,∠D=∠ABE=90°,
∴Rt△AEB≌Rt△AND(SAS),
∴AE=AN,∠EAB=∠NAD,
∵∠DAN+∠BAM=45°,
∴∠EAB+∠BAM=45°,
∴∠EAM=45°,
∴∠EAM=∠NAM=45°,
又AM=AM,
∴△AEM≌△ANM(SAS),
∵AB,AH是△AEM和△ANM对应边上的高,
∴AB=AH.
(3)分别沿AM,AN翻折△AMH和△ANH,得到△ABM和△AND,分别延长BM和DN交于点C,如图:
∵沿AM,AN翻折△AMH和△ANH,得到△ABM和△AND,
∴AB=AH=AD=6,∠BAD=2∠MAN=90°,∠B=∠AHM=90°=∠AHN=∠D,
∴四边形ABCD是正方形,
∴AH=AB=BC=CD=AD=6.
由(2)可知,设NH=x,则MC=BC﹣BM=BC﹣HM=4,NC=CD﹣DN=CD﹣NH=6﹣x,
在Rt△MCN中,由勾股定理,得MN2=MC2+NC2,
∴(2+x)2=42+(6﹣x)2,
解得x=3,
∴NH=3
【变式3-1】探究:
(1)如图1,在正方形ABCD中,E、F分别是BC、CD上的点,且∠EAF=45°,试判断BE、DF与EF三条线段之间的数量关系,直接写出判断结果: ;
(2)如图2,若把(1)问中的条件变为“在四边形ABCD中,AB=AD,∠B+∠D=180°,E、F分别是边BC、CD上的点,且∠EAF=∠BAD”,则(1)问中的结论是否仍然成立?若成立,请给出证明,若不成立,请说明理由;
(3)在(2)问中,若将△AEF绕点A逆时针旋转,当点分别E、F运动到BC、CD延长线上时,如图3所示,其它条件不变,则(1)问中的结论是否发生变化?若变化,请给出结论并予以证明.
【解答】解:(1)如图1,将△ADF绕点A顺时针旋转,使AD与AB重合,得到△ABF′,
∵∠EAF=45°,
∴∠EAF′=∠EAF=45°,
在△AEF和△AEF′中,
,
∴△AEF≌△AEF′(SAS),
∴EF=EF′,
又EF′=BE+BF′=BE+DF,
∴EF=BE+DF;
(2)结论EF=BE+DF仍然成立.
理由如下:如图2,将△ADF绕点A顺时针旋转,使AD与AB重合,得到△ABF′,
则△ADF≌△ABF′,
∴∠BAF′=∠DAF,AF′=AF,BF′=DF,∠ABF′=∠D,
又∵∠EAF=∠BAD,
∴∠EAF=∠DAF+∠BAE=∠BAE+∠BAF′,
∴∠EAF=∠EAF′,
又∵∠ABC+∠D=180°,
∴∠ABF′+∠ABE=180°,
∴F′、B、E三点共线,
在△AEF与△AEF′中,
,
∴△AEF≌△AEF′(SAS),
∴EF=EF′,
又∵EF′=BE+BF′,
∴EF=BE+DF;
(3)发生变化.EF、BE、DF之间的关系是EF=BE﹣DF.
理由如下:如图3,将△ADF绕点A顺时针旋转,使AD与AB重合,点F落在BC上点F′处,得到△ABF′,
∴△ADF≌△ABF′,
∴∠BAF′=∠DAF,AF′=AF,BF′=DF,
又∵∠EAF=∠BAD,且∠BAF′=∠DAF,
∴∠F′AE=∠BAD﹣(∠BAF′+∠EAD)=∠BAD﹣(∠DAF+∠EAD)=∠BAD﹣∠FAE=∠FAE,
即∠F′AE=∠FAE,
在△F′AE与△FAE中,,
∴△F′AE≌△FAE(SAS),
∴EF=EF′,
又∵BE=BF′+EF′,
∴EF′=BE﹣BF′,
即EF=BE﹣DF.
【变式3-2】已知:如图边长为2的正方形ABCD中,∠MAN的两边分别交BC、CD边于M、N两点,且∠MAN=45°
①求证:MN=BM+DN;
②若AM、AN交对角线BD于E、F两点.设BF=y,DE=x,求y与x的函数关系式.
【解答】(1)证明:将△ABM绕点A逆时针旋转90°至△ADM′,
∴∠M′AN=∠DAN+∠MAB=45°,AM′=AM,BM=DM′,
∵M′AN=∠MAN=45°,AN=AN,
∴△AMN≌△AM′N′,
∴MN=NM′,
∴M′N=M′D+DN=BM+DN,
∴MN=BM+DN.
(2)解:∵∠AED=45°+∠BAE,∠FAB=45°+∠BAE,
∴∠AED=∠FAB,
∵∠ABF=∠ADE,
∴△BFA∽△DAE,
∴=,
∴=,
∴y=.
【类型三:等边三角形中120°含60°的半角模型】
【典例4】已知在△ABC中,AB=AC,D,E是BC边上的点,将△ABD绕点A旋转,得到△ACD',连接D'E.
(Ⅰ)如图1,当∠BAC=120°,∠DAE=60°时,求证:DE=D'E;
(Ⅱ)如图2,当DE=D'E时,请写出∠DAE与∠BAC的数量关系,并说明理由.
(Ⅲ)当∠BAC=90°,DE=D'E,EC=CD'时,请直接写出BD与DE的数量关系(不必说明理由).
【解答】(I)证明:∵将△ABD绕点A旋转,得到△ACD',
∴AD=AD',∠CAD'=BAD,
∵∠BAC=120°,∠DAE=60°,
∴∠D'AE=∠CAD'+∠CAE
=∠BAD+∠CAE
=∠BAC﹣∠DAE
=120°﹣60°
=60°,
∴∠DAE=∠D'AE,
在△ADE与△AD'E中,
,
∴△ADE≌△AD'E(SAS),
∴DE=D'E;
(Ⅱ)解:∠DAE=,理由如下:
在△ADE与△AD'E中,
,
∴△ADE≌△AD'E(SSS),
∴∠DAE=∠D'AE,
∴∠BAD+∠CAE=∠CAD'+∠CAE=∠D'AE=∠DAE,
∴∠DAE=;
(Ⅲ)解:DE=BD,理由如下:
∵∠BAC=90°,AB=AC,
∴∠B=∠ACD=45°,
∴∠ECD=90°,
∵EC=CD',
∴△ECD'是等腰直角三角形,
∴D'E=CD'=BD,
∵DE=D'E,
∴DE=BD.
【变式4-1】(2017秋•锦江区期末)在△ABC中,AB=AC,点E,F是边BC所在直线上与点B,C不重合的两点.
(1)如图1,当∠BAC=90°,∠EAF=45°时,直接写出线段BE,CF,EF的数量关系;(不必证明)
(2)如图2,当∠BAC=60°,∠EAF=30°时,已知BE=3,CF=5,求线段EF的长度;
(3)如图3,当∠BAC=90°,∠EAF=135°时,请探究线段CE,BF,EF的数量关系,并证明.
【解答】解:(1)结论:EF2=BE2+CF2.
理由:∵∠BAC=90°,AB=AC,
∴将△ABE绕点A逆时针旋转90°得△ACG,连接FG,如图1中,
∴AG=AE,CG=BE,∠ACG=∠B,∠EAG=90°,
∴∠FCG=∠ACB+∠ACG=∠ACB+∠B=90°,
∴FG2=FC2+CG2=BE2+FC2;
又∵∠EAF=45°,
而∠EAG=90°,
∴∠GAF=90°﹣45°=45°,
∴∠EAF=∠GAF,
∵AF=AF,AE=AG,
∴△AEF≌△AGF(SAS),
∴EF=FG,
∴EF2=BE2+CF2.
(2)如图2中,∵∠BAC=60°,AB=AC,
∴将△ABE绕点A逆时针旋转60°得△ACG,连接FG,作GH⊥BC交BC的延长线于H.
∵∠BAC=60°,∠EAF=30°,
∴∠BAE+∠CAF=∠CAG+∠CAF=∠FAG=30°,
∴∠EAF=∠FAG,
∵AF=AF,AE=AG,
∴△AEF≌△AGF(SAS),
∴EF=FG,
在Rt△CGH中,∵CG=BE=3,∠GCH=60°,
∴∠CGH=30°,
∴CH=CG=,GH=CH=,
在Rt△FGH中,FG===7,
∴EF=FG=7.
(3)结论:EF2=EC2+BF2
理由:如图3中,将△AEC绕点A顺时针旋转90°,得到△ABG,连接FG.
∵AB=AC,∠BAC=90°,
∴∠ABC=∠ACB=45°,
∵△ACE≌△ABG,
∴∠CAE=∠BAG,EC=BG,∠ACE=∠ABG=45°,
∴∠CAB=∠EAG=90°,∠GBF=90°,
∴∠FAG=360°﹣∠EAF﹣∠EAG=360°﹣135°﹣90°=135°,
∴∠FAE=∠FAG,
∵FA=FA,AG=AE,
∴△FAE≌△FAG(SAS),
∴EF=FG,
在Rt△FBG中,∵∠FBG=90°,
∴FG2=BG2+BF2,
∵FG=EF,BG=EC,
∴EF2=EC2+BF2.
【变式4-2】等边△ABC,D为△ABC外一点,∠BDC=120°,BD=DC,∠MDN=60°,射线DM与直线AB相交于点M,射线DN与直线AC相交于点N,
①当点M、N在边AB、AC上,且DM=DN时,直接写出BM、NC、MN之间的数量关系.
②当点M、N在边AB、AC上,且DM≠DN时,猜想①中的结论还成立吗?若成立,请证明.
③当点M、N在边AB、CA的延长线上时,请画出图形,并写出BM、NC、MN之间的数量关系.
【解答】解①BM、NC、MN之间的数量关系 BM+NC=MN.
②猜想:结论仍然成立.
证明:在CN的反向延长线上截取CM1=BM,连接DM1.
∵∠MBD=∠M1CD=90°,BD=CD,
∴△DBM≌△DCM1,
∴DM=DM1,∠MBD=∠M1CD,M1C=BM,
∵∠MDN=60°,∠BDC=120°,
∴∠M1DN=∠MDN=60°,
∴△MDN≌△M1DN,
∴MN=M1N=M1C+NC=BM+NC,
③证明:在CN上截取CM1=BM,连接DM1.
可证△DBM≌△DCM1,
∴DM=DM1,
可证∠M1DN=∠MDN=60°,
∴△MDN≌△M1DN,
∴MN=M1N,
∴NC﹣BM=MN.
从正方形的一个顶点引出夹角为45°的两条射线,并连接它们与该顶点的两对边的交点构成的基本平面几何模型称为半角模型.半角模型可证出多个几何结论,例如:
如图1,在正方形ABCD中,以A为顶点的∠EAF=45°,AE、AF与BC、CD边分别交于E、F两点.易证得EF=BE+FD.
大致证明思路:如图2,将△ADF绕点A顺时针旋转90°,得到△ABH,由∠HBE=180°可得H、B、E三点共线,∠HAE=∠EAF=45°,进而可证明△AEH≌△AEF,故EF=BE+DF.
从正方形的一个顶点引出夹角为45°的两条射线,并连接它们与该顶点的两对边的交点构成的基本平面几何模型称为半角模型.半角模型可证出多个几何结论,例如:
如图1,在正方形ABCD中,以A为顶点的∠EAF=45°,AE、AF与BC、CD边分别交于E、F两点.易证得EF=BE+FD.
大致证明思路:如图2,将△ADF绕点A顺时针旋转90°,得到△ABH,由∠HBE=180°可得H、B、E三点共线,∠HAE=∠EAF=45°,进而可证明△AEH≌△AEF,故EF=BE+DF.
2024年中考数学专题训练 专题10 截长补短模型综合应用(知识解读): 这是一份2024年中考数学专题训练 专题10 截长补短模型综合应用(知识解读),共30页。
2024年中考数学专题训练 专题06 半角模型综合应用(专项训练)(原卷版+解析): 这是一份2024年中考数学专题训练 专题06 半角模型综合应用(专项训练)(原卷版+解析),共16页。试卷主要包含了已知等内容,欢迎下载使用。
2024年中考数学专题训练 专题06 半角模型综合应用(能力提升)(原卷版+解析): 这是一份2024年中考数学专题训练 专题06 半角模型综合应用(能力提升)(原卷版+解析),共24页。试卷主要包含了如图,问题提出等内容,欢迎下载使用。












