2024年中考数学专题训练 专题02 线圆最值（知识解读）

这是一份2024年中考数学专题训练 专题02 线圆最值（知识解读），共14页。
直线与圆的位置关系是中考数学一个非常重要的 内容，它涉及的知识点较多，题型也千变万化.最值是数学知识体系中的重要内容，也是数学中最具挑战性的问题.中考命题者对直线与圆知识中的最值问题常常是情有独钟，这种导向性使得该知识成为教学中的重点与难点.从问题解决的思路来看，学生要想顺利地解决此类 问题，需要综合运用几何与代数的相关知识与方法，以及数形结合等思想，并在此过程中寻找到解决最值问题的方法.本文通过教学实践，枚举几例直线与圆中的最值问题，以供参考.
【方法技巧】
考点：线圆最值
已知O及直线l，O的半径为r，点Q为O上一点，圆心O与直线l之间的距离为d.
拓展：在解决某些面积最值问题时，常利用此模型，将问题转化为求动点到定边的最大（小）距离，进而利用面积公式求解
【典例分析】
【典例1】如图，在矩形ABCD中，BC＝2AB＝4，点E是AB的中点，点P是矩形ABCD内一点，且EP＝AE，连接CP，PD，则△PCD面积的最小值为 ．
【典例2】如图，在△ABC和△ADE中，AB＝AC＝6，AD＝AE，∠BAC＝∠DAE＝60°，且BD＝2AD，DE∥BC，点M是DE的中点，连接BM，CM．将△ADE绕点A逆时针旋转，则在旋转过程中，△BMC面积的最大值为 ．
【典例3】如图，在矩形ABCD中，AB＝3，BC＝4，点P是矩形ABCD内一点，且∠BPC＝90°，连接AP，PD，则△APD面积的最小值为 ．
【典例4】如图，在边长为2的菱形ABCD中，∠A＝60°，点M是AD边的中点，点N是AB边上一动点，将△AMN沿MN所在直线翻折得到△A'MN，连接A'B，A'C，则△A'BC面积的最小值为 ．
【典例5】如图，在Rt△ABC中，AB＝3，BC＝4，点D是AC边上一点，点E是平面内一点，且DE＝1，连接AE，CE，则四边形ABCE面积的最大值为 ．
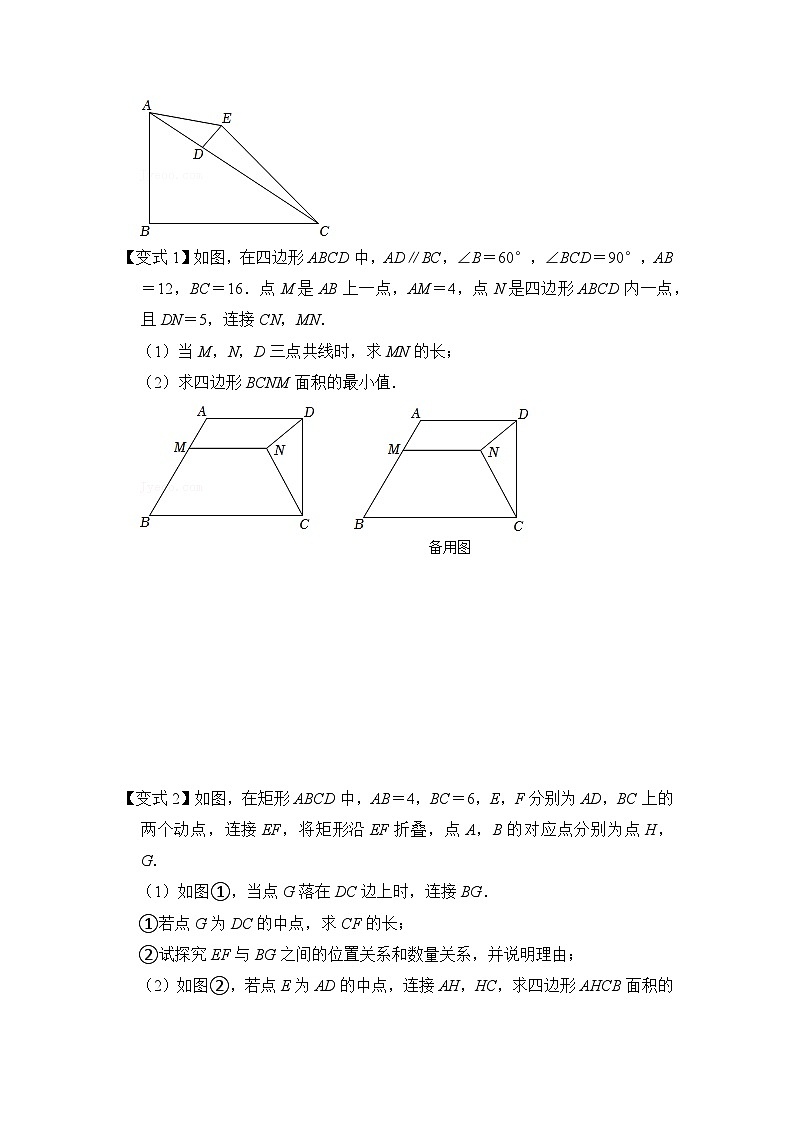
【变式1】如图，在四边形ABCD中，AD∥BC，∠B＝60°，∠BCD＝90°，AB＝12，BC＝16．点M是AB上一点，AM＝4，点N是四边形ABCD内一点，且DN＝5，连接CN，MN．
（1）当M，N，D三点共线时，求MN的长；
（2）求四边形BCNM面积的最小值．
【变式2】如图，在矩形ABCD中，AB＝4，BC＝6，E，F分别为AD，BC上的两个动点，连接EF，将矩形沿EF折叠，点A，B的对应点分别为点H，G．
（1）如图①，当点G落在DC边上时，连接BG．
①若点G为DC的中点，求CF的长；
②试探究EF与BG之间的位置关系和数量关系，并说明理由；
（2）如图②，若点E为AD的中点，连接AH，HC，求四边形AHCB面积的最大值．
专题02 线圆最值（知识解读）
【专题说明】
直线与圆的位置关系是中考数学一个非常重要的 内容，它涉及的知识点较多，题型也千变万化.最值是数学知识体系中的重要内容，也是数学中最具挑战性的问 题.中考命题者对直线与圆知识中的最值问题常常是情有独钟，这种导向性使得该知识成为教学中的重点与难点.从问题解决的思路来看，学生要想顺利地解决此类 问题，需要综合运用几何与代数的相关知识与方法，以及数形结合等思想，并在此过程中寻找到解决最值问题的方法.本文通过教学实践，枚举几例直线与圆中的最值问题，以供参考.
【方法技巧】
考点：线圆最值
已知O及直线l，O的半径为r，点Q为O上一点，圆心O与直线l之间的距离为d.
拓展：在解决某些面积最值问题时，常利用此模型，将问题转化为求动点到定边的最大（小）距离，进而利用面积公式求解
【典例分析】
【典例1】如图，在矩形ABCD中，BC＝2AB＝4，点E是AB的中点，点P是矩形ABCD内一点，且EP＝AE，连接CP，PD，则△PCD面积的最小值为 ．
【答案】3
【解答】解：∵BC＝2AB＝4，
∴AB＝2，
•点E是AB 的中点，
∴AE＝BE＝1．；
∴点P在以点E为圆心，1为半径的弧上运动，
过点 P作PQ⊥CD 于点Q，
过点E作EF⊥CD于点F，
则＝PQ，
∴当PQ最小时，△PCD 的面积取得最小值•EP+PQ≥EF，
当E，P，Q三点共线时，PQ取得最小值，最小值为EF﹣EP的值；
∴四边形ABCD是矩形，
∴EF＝BC＝4，
∴PQ最小＝EF﹣EP＝3，
∴S△PCD最小＝PQ最小＝3，
故答案为：3．
【典例2】如图，在△ABC和△ADE中，AB＝AC＝6，AD＝AE，∠BAC＝∠DAE＝60°，且BD＝2AD，DE∥BC，点M是DE的中点，连接BM，CM．将△ADE绕点A逆时针旋转，则在旋转过程中，△BMC面积的最大值为 ．
【答案】12．
【解答】解：连接AM，交BC于H，.
∵AB＝AC，AD＝AE，点M是DE的中点，
∴AM⊥DE，AH⊥BC，
将△ADE绕点A逆时针旋转180°，即M'、M、H在同一直线上时，△BMC面积取最大值．
∵AB＝AC＝6，AD＝AE，∠BAC＝∠DAE＝60°，且BD＝2AD，
∴AD＝AE＝2，BH＝＝＝3，
∴AM＝AD＝＝，
∴AM'＝，
∴M'H＝＝4，
此时，△BMC面积＝＝＝12．
故答案为：12．
【典例3】如图，在矩形ABCD中，AB＝3，BC＝4，点P是矩形ABCD内一点，且∠BPC＝90°，连接AP，PD，则△APD面积的最小值为 ．
【答案】2
【解答】解：∵∠BPC＝90°，
∴点P在以BC为直径的圆上，
即点P到BC的最大距离为2，
∴点P到AD的最小值＝3﹣×4＝1，
∴S△APD＝×4×1＝2，
∴△APD面积的最小值为2．
故答案为：2．
【典例4】如图，在边长为2的菱形ABCD中，∠A＝60°，点M是AD边的中点，点N是AB边上一动点，将△AMN沿MN所在直线翻折得到△A'MN，连接A'B，A'C，则△A'BC面积的最小值为 ．
【答案】﹣1
【解答】解：如图，
由折叠知A'M＝AM，
又∵M是AD的中点，
∴MA＝MA'＝MD，
点A'的运动轨迹就是在以点M为圆心，MA长为半径的上，
过点M作ME⊥BC于点E，连接BD，
在菱形ABCD中，
∵AD＝AB，∠A＝60°，
∴△ABD是等边三角形．
∵M是AD的中点，
∴点E与点B重合，
∴EM＝，
设点A'到BC的距离为h，当点A'在ME上时，h取得最小值，最小值为EM﹣A'M＝﹣1，
∴△A'BC面积的最小值为＝BC•h＝×2×（﹣1）＝﹣1，
故答案为：﹣1．
【典例5】如图，在Rt△ABC中，AB＝3，BC＝4，点D是AC边上一点，点E是平面内一点，且DE＝1，连接AE，CE，则四边形ABCE面积的最大值为 ．
【答案】
【解答】解：∵在Rt△ABC中，∠B＝90°，AB＝3，BC＝4，
∴AC＝．
经分析，当DE⊥AC于D时，四边形ABCE面积的最大．
∴四边形ABCE面积的最大值为S四边形ABCE＝S△ABC+S△ACE＝DE＝＝．
故答案为：．
【变式1】如图，在四边形ABCD中，AD∥BC，∠B＝60°，∠BCD＝90°，AB＝12，BC＝16．点M是AB上一点，AM＝4，点N是四边形ABCD内一点，且DN＝5，连接CN，MN．
（1）当M，N，D三点共线时，求MN的长；
（2）求四边形BCNM面积的最小值．
【解答】解：（1）延长DA到F，作MG⊥AF于G，AE⊥BC于E，
∵∠B＝60°，AB＝12，
∴BE＝6．
∴AD＝EC＝10，
∵AM＝4，∠AMG＝30°，
∴AG＝2，MG＝2，
∴DG＝12，
∵DM2＝DG2+MG2，
∴DM2＝122+（2）2，
∴DM＝2，
∴MN＝2﹣5；
（2）取BC中点K，连接MC，MK，作NH⊥MC于H，DL⊥MC于L，
∵∠B＝60°，BM＝BK＝8，
∴△MBK是等边三角形，
∴MK＝KC＝6，
∠MKB＝60°，
∴∠KMC＝∠MCK＝30°，
∴∠BMC＝90°
∴MC＝8，
∴S△MBC＝MC•MB＝32，
∴当△NMC面积最小时，四边形MBCN面积最小，
∵DN＝5，
∴当D，N，H三点共线时，NH最小，
△NMC面积最小，
由（1）知DC＝AE＝6，
∴DL＝DC＝9，
∴NH最小值为：4，
∴S△NMC的最小值为：CM•NH＝16，
∴四边形MBCN面积最小值为：32+16＝48．
【变式2】如图，在矩形ABCD中，AB＝4，BC＝6，E，F分别为AD，BC上的两个动点，连接EF，将矩形沿EF折叠，点A，B的对应点分别为点H，G．
（1）如图①，当点G落在DC边上时，连接BG．
①若点G为DC的中点，求CF的长；
②试探究EF与BG之间的位置关系和数量关系，并说明理由；
（2）如图②，若点E为AD的中点，连接AH，HC，求四边形AHCB面积的最大值．
【解答】解：（1）①如图①中，∵四边形ABCD是矩形，
∴∠C＝90°，AB＝CD＝4，BC＝6，
∵DG＝CG＝2，
由翻折的性质可知，FB＝FG，
设FB＝FG＝x，
∵FG2＝CG2+CF2，
∴x2＝（6﹣x）2+22，
∴x＝，
∴CF＝6﹣＝；
②结论：EF⊥BG，＝．
理由：如图①中，过点E作ET⊥BC于点T，设BG交ET于点J，BG交EF于点O，则四边形ABTE是矩形，ET＝AB＝4．
由翻折变换的性质可知，EF垂直平分线段BG，
∴∠EOJ＝∠BTJ＝90°，
∵∠EJO＝∠BJT，
∴∠FET＝∠CBG，
∵∠ETF＝∠C＝90°，
∴△ETF∽△BCG，
∴＝＝＝；
（2）如图②中，连接AC，过点E作ER⊥AC于点R．
在Rt△ADC中，AD＝6，CD＝4，
∴AC＝＝＝2，
∵sin∠EAR＝＝，AE＝ED＝3，
∴＝，
∴ER＝，
∵EH＝AE＝3，
∴当点H在RE的延长线上时，△ACH的面积最大，此时四边形ABCH的面积最大，
∴四边形ABCH的面积的最大值＝×4×6+×2×（+3）＝18+3．
位置关系
直线与O相离
直线与O相切
直线与O相交
图示
点Q到直线l距离的最大值
d＋r
2r
d＋r
此时点Q的位置
过点O作直线l的垂线，其反向延长线与O的交点，即为点Q
点Q到直线l距离的最小值
d－r
0
r－d
此时点Q的位置
过点O作直线l的垂线，与O的交点即为点Q
位置关系
直线与O相离
直线与O相切
直线与O相交
图示
点Q到直线l距离的最大值
d＋r
2r
d＋r
此时点Q的位置
过点O作直线l的垂线，其反向延长线与O的交点，即为点Q
点Q到直线l距离的最小值
d－r
0
r－d
此时点Q的位置
过点O作直线l的垂线，与O的交点即为点Q