
河南省信阳市罗山县2023-2024学年九年级上学期期末数学试题
展开一、选择题(每小题3分,共30分)
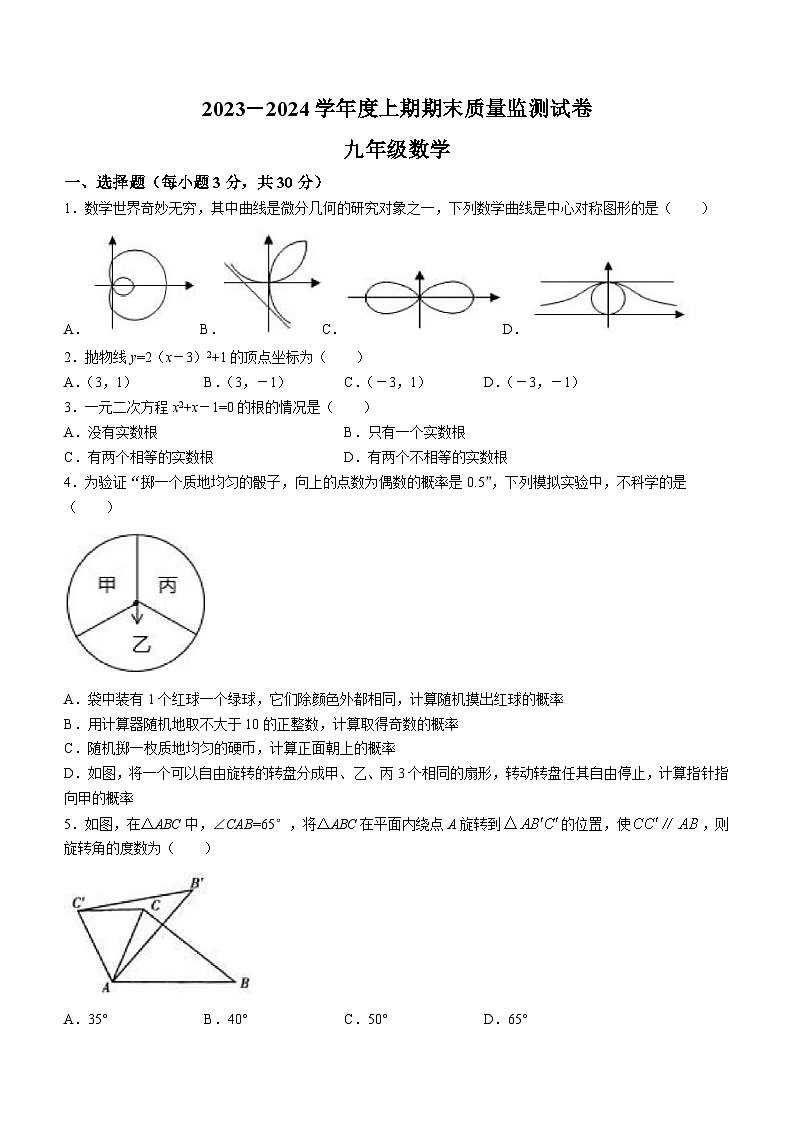
1.数学世界奇妙无穷,其中曲线是微分几何的研究对象之一,下列数学曲线是中心对称图形的是( )
A.B.C.D.
2.抛物线y=2(x-3)2+1的顶点坐标为( )
A.(3,1)B.(3,-1)C.(-3,1)D.(-3,-1)
3.一元二次方程x2+x-1=0的根的情况是( )
A.没有实数根B.只有一个实数根
C.有两个相等的实数根D.有两个不相等的实数根
4.为验证“掷一个质地均匀的骰子,向上的点数为偶数的概率是0.5”,下列模拟实验中,不科学的是( )
A.袋中装有1个红球一个绿球,它们除颜色外都相同,计算随机摸出红球的概率
B.用计算器随机地取不大于10的正整数,计算取得奇数的概率
C.随机掷一枚质地均匀的硬币,计算正面朝上的概率
D.如图,将一个可以自由旋转的转盘分成甲、乙、丙3个相同的扇形,转动转盘任其自由停止,计算指针指向甲的概率
5.如图,在△ABC中,∠CAB=65°,将△ABC在平面内绕点A旋转到的位置,使,则旋转角的度数为( )
A.35°B.40°C.50°D.65°
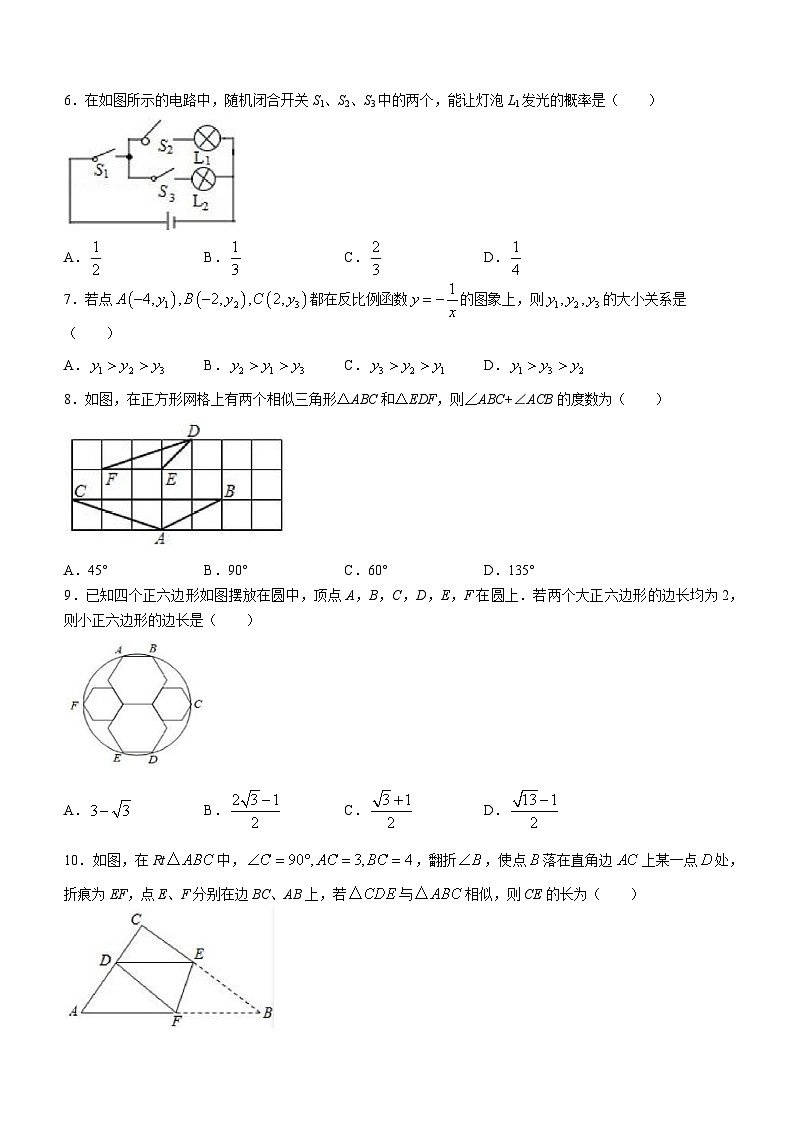
6.在如图所示的电路中,随机闭合开关S1、S2、S3中的两个,能让灯泡L1发光的概率是( )
A.B.C.D.
7.若点都在反比例函数的图象上,则的大小关系是( )
A.B.C.D.
8.如图,在正方形网格上有两个相似三角形△ABC和△EDF,则∠ABC+∠ACB的度数为( )
A.45°B.90°C.60°D.135°
9.已知四个正六边形如图摆放在圆中,顶点A,B,C,D,E,F在圆上.若两个大正六边形的边长均为2,则小正六边形的边长是( )
A.B.C.D.
10.如图,在Rt中,,翻折,使点落在直角边上某一点处,折痕为EF,点E、F分别在边BC、AB上,若与相似,则CE的长为( )
A.B.或C.或D.
二、填空题(本大题共10小题,共30分.)
11.反比例函数的图象在第二、四象限内,那么的取值范围是______.
12.方程是关于的一元二次方程,则的值为______.
13.根据物理学规律,如果不考虑空气阻力,以40m/s的速度将小球沿与地面成30°角的方向击出,小球的飞行高度h(单位:m)与飞行时间t(单位:s)之间的函数关系是:h=-5t2+20t,则小球运动中的最大高度是______m.
14.党的二十大胜利召开,学校推荐了四部影片:《1921》、《香山叶正红》、《建党伟业》、《建军大业》.甲、乙同学用抽卡片的方式决定本班观看哪部,四张卡片正面分别是上述影片剧照,除此之外完全相同.将这四张卡片背面朝上,甲随机抽出一张并放回,洗匀后,乙再随机抽出一张,则两人恰好抽到同一部的概率是______.
15.如图,在边长为4的正方形ABCD中,以AB为直径的半圆交对角线AC于点E,以C为圆心、BC长为半径画弧交AC于点F,则图中阴影部分的面积是______.
三、解答题(本大题共10小题,共30分.)
16.(10分)用适当的方法解下列方程:
(1)(x-1)2=4;(2)x2-3x-4=0.
17.(9分)为了保护学生视力,防止学生沉迷网络和游戏,促进学生身心健康发展.学校组织该主题漫画比赛.现在小雪和小英想通过设计一个游戏来决定谁去参赛.游戏规则如下:有一个可自由转动的转盘,被分成了三个大小相同的扇形,分别标有数字2,3,4;另有一个不透明的瓶子,装有分别标有数字1,3,5的三个完全相同的小球.先转动一次转盘,停止后记下指针指向的数字(若指针指在分界线上则重转),再从瓶子中随机取出一个小球,记下小球上的数字.若得到的两数字之和大于6,则小雪参赛;若得到的两数字之和小于6,则小英参赛.
(1)请用列表或画树状图的方法表示出所有可能出现的结果;
(2)此游戏公平吗?请说明理由.
18.(9分)如图,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(1,3),B(2,5),C(4,2)(每个方格的边长均为1个单位长度)
(1)将△ABC平移,使点A移动到点A1,请画出△A1B1C1;
(2)作出△ABC关于O点成中心对称的△A2B2C2,并直接写出A2,B2,C2的坐标;
(3)△A1B1C1与△A2B2C2是否成中心对称?若是,请写出对称中心的坐标;若不是,请说明理由.
19.(9分)实验数据显示,一般成人喝半斤低度白酒后,1.5小时内其血液中酒精含量y(毫克/百毫升)与时间x(时)的关系可近似地用二次函数y=-200x2+400x来刻画:1.5小时后(包括1.5小时)y与x可近似地用反比例函数(k>0)刻画.
(1)根据上述数学模型计算:
①喝酒后几小时血液中的酒精含量达到最大值?最大值为多少?
②当x=5时,y=45,求k的值.
(2)按国家规定,车辆驾驶人员血液中的酒精含量大于或等于20毫克/百毫升时属于“酒后驾驶”,不能驾车上路.参照上述数学模型,假设某驾驶员晚上20:00在家喝完半斤低度白酒,第二天早上7:00能否驾车去上班?请说明理由.
20.(9分)阅读下面材料,完成学习任务:
数学活动 测量树的高度
在物理学中我们学过光的反射定律.数学综合实践小组想利用光的反射定律测量池塘对岸一棵树的高度AB测量和计算的部分步骤如下:
①如图,在地面上的点C处放置了一块平面镜,小华站在BC的延长线上,当小华从平面镜中刚好看到树的顶点A时.测得小华到平面镜的距离CD=2米,小华的眼睛E到地面的距离ED=1.5米;
②将平面镜从点C沿BC的延长线向后移动10米到点F处,小华向后移动到点H处时,小华的眼睛G又刚好在平面镜中看到树的顶点A,这时测得小华到平面镜的距离FH=3米;
③计算树的高度AB:设AB=x米,BC=y米.
∵∠ABC=∠EDC=90°,∠ACB=∠ECD
∴△ABC∽△EDC
…….
任务:请你根据材料中得到的测量数据和计算步骤,将剩余的计算部分补充完整.
21.(9分)如图,AB是⊙O的直径,BD是⊙O的弦,延长BD到点C,使DC=BD,连结AC,过点D作DE⊥AC,垂足为E.
(1)求证:AB=AC;
(2)求证:DE为⊙O的切线:
(3)若⊙O的半径为5,∠BAC=60°,求DE的长.
22.(10分)
根据以下素材,探索完成任务.
23.(10分)
图1 图2 图3
【操作发现】
(1)如图1,在边长为1个单位长度的小正方形组成的网格中,△ABC的三个顶点均在格点上.
①请按要求画图:将ABC绕点A按顺时针方向旋转90°,点B的对应点为,点C的对应点为;
②连接,此时=______°;
【问题解决】
在某次数学兴趣小组活动中,小明同学遇到了如下问题:
(2)如图2,在等边△ABC中,点P在内部,且PA=3,PC=4,∠APC=150°,求PB的长.
经过同学们的观察、分析、思考、交流,对上述问题形成了如下想法:将△APC绕点A按顺时针方向旋转60°,得到,连接,寻找PA、PB、PC三边之间的数量关系.…请参考他们的想法,完成该问题的解答过程;
【学以致用】
(3)如图3,在等腰直角△ABC中,∠ACB=90°,P为△ABC内一点,且PA=5,,∠BPC=135°,求PB.
2023-2024学年度上期期末质量监测试卷
九年级数学参考答案
一、选择题(共10小题)
1.C 2.A 3.D 4.D 5.C 6.B 7.B 8.A 9.D 10.B
二、填空题(共5小题)
11.m<5 12.-2. 13.20 14. 15.
三、解答题(共75分)
16.解:(1)(x-1)2=4,或
(2),或,.
17.解:(1)画树状图如下:
和
共有9种等可能的结果;(4分)
(2)此游戏公平,理由如下:(5分)
共有9种等可能的结果,两数字之和大于6的结果有4种,两数字之和小于6的结果有4种,
小雪参赛的概率为,小英参赛的概率为,
此游戏公平.
18.解:(1)如图,为所作;
(2)如图,为所作;
点的坐标分别为;
(3)与关于点中心对称,
如图,对称中心的坐标的坐标为.
19.解:(1)①,
时血液中的酒精含量达到最大值,最大值为200毫克/百毫升;
②当时,,;
(2)不能驾车上班;
理由:∵晚上20:00到第二天早上7:00,一共有11小时,
将代入,则,
第二天早上7:00不能驾车去上班.
20.解:设AB=x米,BC=y米.
∴△ABC∽△EDC
,,
,
,,
解得,把代入中,得解得
树的高度AB为15米.
21.(1)证明:如图1,连接AD,
∵AB是⊙O的直径,∴AD⊥BC,又DC=BD,
在△ADC和△ADB中,,
∴△ADC≌△ADB(SAS),∴AB=AC;
(2)证明:如图2,连接OD,
∵AO=BO,CD=DB,∴OD是△ABC的中位线,
∴,又DE⊥AC,∴DE⊥OD,
∴DE为⊙O的切线;(6分)
(3)解:∵AB=AC,∠BAC=60°,
∴△ABC是等边三角形,∴BC=AC=AB=10,
∴CD=5,∵△ABC是等边三角形,
∴∠C=60°,在Rt△DEC中,:∠CDE=30°,
,.
图1 图2
22.解:(1)建立直角坐标系如图(答案不唯一):
由已知可得,顶点的横坐标为3.5,
设大棚横截面所对应的抛物线解析式为,
,解得,
大棚横截面所对应的抛物线解析式为;
(2)符合要求的方案(答案不唯一):
从距左侧墙体2米处立第一根竹竿,距左侧墙体4米处立第二根竹竿,∴共需2根竹竿,
当时,,
当时,,
所需竹竿总长度为(米).
23.解:(1)①如图1所示,即为所求;
图1
②45
(2)如图2,
∵将△APC绕点A按顺时针方向旋转60°得到,
∴,,,∴是等边三角形,
因此,,
又∵,∴,
.
图2
(3)是等腰直角三角形,.
将三角形ACP绕点顺时针旋转得到,连接,如图
则,
,
是等腰直角三角形,.如何加固蔬菜大棚?
素材1
农科所在某蔬菜基地试用新型保温大棚技术.大棚横截面为抛物线型(如图),一端固定在距离地面1米的墙体A处.另一端固定在距离地面2米的对面墙体B处,两墙体的水平距离为6米.大棚离地面的最高点P与A的水平距离为3.5米.
素材2
为了使大棚更牢固,在此横截面内竖立若干根与地面垂直的竹竿连接到大棚的边缘.要求相邻竹竿之间的水平距离为2米,靠近墙体的竹竿与墙体的水平距离不超过2米.
问题解决
任务1
确定大棚形状
结合素材1,在图中建立合适的直角坐标系,求大棚横截面所对应的抛物线解析式(不需写自变量取值范围)
任务2
探索加固方案
请你设计一个符合要求的竹竿竖立方案,方案内容包括:
①从何处立第一根竹竿;
②共需多少根竹竿;
③所需学竹竿的总长度(写出计算过程).
河南省信阳市罗山县实验中学2023-2024学年九年级下学期开学数学试题: 这是一份河南省信阳市罗山县实验中学2023-2024学年九年级下学期开学数学试题,共6页。
精品解析:河南省信阳市罗山县2023-2024学年九年级上学期期末数学试题: 这是一份精品解析:河南省信阳市罗山县2023-2024学年九年级上学期期末数学试题,文件包含精品解析河南省信阳市罗山县2023-2024学年九年级上学期期末数学试题原卷版docx、精品解析河南省信阳市罗山县2023-2024学年九年级上学期期末数学试题解析版docx等2份试卷配套教学资源,其中试卷共30页, 欢迎下载使用。
河南省信阳市罗山县2023-2024学年七年级上学期期末数学试题(含答案): 这是一份河南省信阳市罗山县2023-2024学年七年级上学期期末数学试题(含答案),共16页。试卷主要包含了单选题,填空题,解答题等内容,欢迎下载使用。












