湖北省各地市2023中考数学真题分类汇编02填空题（基础题）知识点分类②

这是一份湖北省各地市2023中考数学真题分类汇编02填空题（基础题）知识点分类②，共18页。试卷主要包含了×2＝　 　等内容，欢迎下载使用。

1．（2023•随州）计算：（﹣2）2+（﹣2）×2＝ ．
二．科学记数法—表示较大的数（共1小题）
2．（2023•襄阳）5月5日，记者从襄阳市文化和旅游局获悉，五一长假期间，我市41家A级景区全部开放，共接待游客约2270000人次．数据2270000用科学记数法表示为 ．
三．算术平方根（共1小题）
3．（2023•湖北）请写出一个正整数m的值使得是整数：m＝ ．
四．规律型：数字的变化类（共1小题）
4．（2023•随州）某天老师给同学们出了一道趣味数学题：
设有编号为1﹣100的100盏灯，分别对应着编号为1﹣100的100个开关，灯分为“亮”和“不亮”两种状态，每按一次开关改变一次相对应编号的灯的状态，所有灯的初始状态为“不亮”．现有100个人，第1个人把所有编号是1的整数倍的开关按一次，第2个人把所有编号是2的整数倍的开关按一次，第3个人把所有编号是3的整数倍的开关按一次，……，第100个人把所有编号是100的整数倍的开关按一次．问最终状态为“亮”的灯共有多少盏？
几位同学对该问题展开了讨论：
甲：应分析每个开关被按的次数找出规律；
乙：1号开关只被第1个人按了1次，2号开关被第1个人和第2个人共按了2次，3号开关被第1个人和第3个人共按了2次，……
丙：只有按了奇数次的开关所对应的灯最终是“亮”的状态．
根据以上同学的思维过程，可以得出最终状态为“亮”的灯共有 盏．
五．规律型：图形的变化类（共1小题）
5．（2023•十堰）用火柴棍拼成如图图案，其中第①个图案由4个小等边三角形围成1个小菱形，第②个图案由6个小等边三角形围成2个小菱形，…，若按此规律拼下去，则第n个图案需要火柴棍的根数为 ．（用含n的式子表示）
六．因式分解的应用（共1小题）
6．（2023•十堰）若x+y＝3，xy＝2，则x2y+xy2的值是 ．
七．反比例函数系数k的几何意义（共1小题）
7．（2023•湖北）在平面直角坐标系xOy中，若反比例函数y＝（k≠0）的图象经过点A（﹣1，﹣2）和点B（2，m），则△AOB的面积为 ．
八．反比例函数图象上点的坐标特征（共1小题）
8．（2023•襄阳）点A（1，y1），B（2，y2）都在反比例函数的图象上，则y1 y2．（填“＞”或“＜”）
九．反比例函数与一次函数的交点问题（共1小题）
9．（2023•荆州）如图，点A（2，2）在双曲线y＝（x＞0）上，将直线OA向上平移若干个单位长度交y轴于点B，交双曲线于点C．若BC＝2，则点C的坐标是 ．
一十．三角形内角和定理（共1小题）
10．（2023•十堰）一副三角板按如图所示放置，点A在DE上，点F在BC上，若∠EAB＝35°，则∠DFC＝ ．
一十一．菱形的性质（共1小题）
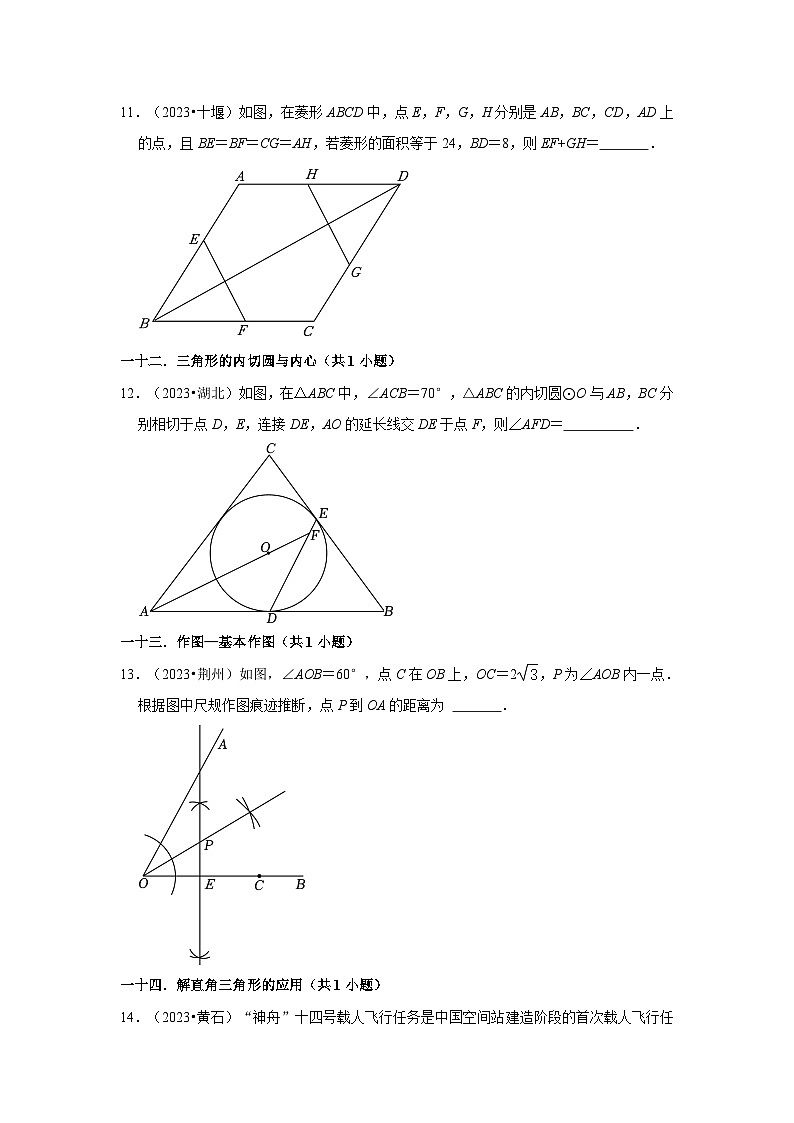
11．（2023•十堰）如图，在菱形ABCD中，点E，F，G，H分别是AB，BC，CD，AD上的点，且BE＝BF＝CG＝AH，若菱形的面积等于24，BD＝8，则EF+GH＝ ．
一十二．三角形的内切圆与内心（共1小题）
12．（2023•湖北）如图，在△ABC中，∠ACB＝70°，△ABC的内切圆⊙O与AB，BC分别相切于点D，E，连接DE，AO的延长线交DE于点F，则∠AFD＝ ．
一十三．作图—基本作图（共1小题）
13．（2023•荆州）如图，∠AOB＝60°，点C在OB上，OC＝2，P为∠AOB内一点．根据图中尺规作图痕迹推断，点P到OA的距离为 ．
一十四．解直角三角形的应用（共1小题）
14．（2023•黄石）“神舟”十四号载人飞行任务是中国空间站建造阶段的首次载人飞行任务，也是空间站在轨建造以来情况最复杂、技术难度最高、航天员乘组工作量最大的一次载人飞行任务．如图，当“神舟”十四号运行到地球表面P点的正上方的F点处时，从点F能直接看到的地球表面最远的点记为Q点，已知PF＝km，∠FOQ＝20°，cs20°≈0.9，则圆心角∠POQ所对的弧长约为 km（结果保留π）．
一十五．解直角三角形的应用-仰角俯角问题（共2小题）
15．（2023•湖北）综合实践课上，航模小组用航拍无人机进行测高实践．如图，无人机从地面CD的中点A处竖直上升30米到达B处，测得博雅楼顶部E的俯角为45°，尚美楼顶部F的俯角为30°，已知博雅楼高度CE为15米，则尚美楼高度DF为 米．（结果保留根号）
16．（2023•黄石）如图，某飞机于空中A处探测到某地面目标在点B处，此时飞行高度AC＝1200米，从飞机上看到点B的俯角为37°，飞机保持飞行高度不变，且与地面目标分别在两条平行直线上同向运动．当飞机飞行943米到达点D时，地面目标此时运动到点E处，从点E看到点D的仰角为47.4°，则地面目标运动的距离BE约为 米．（参考数据：tan37°≈，tan47.4°≈）
一十六．用样本估计总体（共1小题）
17．（2023•荆州）某校为了解学生对A，B，C，D四类运动的参与情况，随机调查了本校80名学生，让他们从中选择参与最多的一类，得到对应的人数分别是30，20，18，12．若该校有800名学生，则估计有 人参与A类运动最多．
一十七．条形统计图（共1小题）
18．（2023•宜昌）如图，条形图描述了某车间工人日加工零件数的情况．这些工人日加工零件数的中位数是 ．
一十八．中位数（共1小题）
19．（2023•湖北）眼睛是心灵的窗户，为保护学生视力，启航中学每学期给学生检查视力，下表是该校某班39名学生右眼视力的检查结果，这组视力数据中，中位数是 ．
一十九．众数（共1小题）
20．（2023•鄂州）为了加强中学生“五项管理”，葛洪学校就“作业管理”、“睡眠管理”、“手机管理”、“读物管理”、“体质管理”五个方面对各班进行考核打分（各项满分均为100），九（1）班的五项得分依次为95，90，85，90，92，则这组数据的众数是 ．
湖北省各地市2023-中考数学真题分类汇编-02填空题（基础题）知识点分类②
参考答案与试题解析
一．有理数的混合运算（共1小题）
1．（2023•随州）计算：（﹣2）2+（﹣2）×2＝ 0 ．
【答案】0．
【解答】解：（﹣2）2+（﹣2）×2
＝4+（﹣4）
＝0．
故答案为：0．
二．科学记数法—表示较大的数（共1小题）
2．（2023•襄阳）5月5日，记者从襄阳市文化和旅游局获悉，五一长假期间，我市41家A级景区全部开放，共接待游客约2270000人次．数据2270000用科学记数法表示为 2.27×106 ．
【答案】2.27×106．
【解答】解：2270000用科学记数法表示为 2.27×106，
故答案为：2.27×106．
三．算术平方根（共1小题）
3．（2023•湖北）请写出一个正整数m的值使得是整数：m＝ 2（答案不唯一） ．
【答案】2（答案不唯一）．
【解答】解：写出一个正整数m的值使得是整数：m＝2（答案不唯一）．
故答案为：2（答案不唯一）．
四．规律型：数字的变化类（共1小题）
4．（2023•随州）某天老师给同学们出了一道趣味数学题：
设有编号为1﹣100的100盏灯，分别对应着编号为1﹣100的100个开关，灯分为“亮”和“不亮”两种状态，每按一次开关改变一次相对应编号的灯的状态，所有灯的初始状态为“不亮”．现有100个人，第1个人把所有编号是1的整数倍的开关按一次，第2个人把所有编号是2的整数倍的开关按一次，第3个人把所有编号是3的整数倍的开关按一次，……，第100个人把所有编号是100的整数倍的开关按一次．问最终状态为“亮”的灯共有多少盏？
几位同学对该问题展开了讨论：
甲：应分析每个开关被按的次数找出规律；
乙：1号开关只被第1个人按了1次，2号开关被第1个人和第2个人共按了2次，3号开关被第1个人和第3个人共按了2次，……
丙：只有按了奇数次的开关所对应的灯最终是“亮”的状态．
根据以上同学的思维过程，可以得出最终状态为“亮”的灯共有 10 盏．
【答案】10．
【解答】解：∵1号开关被按了1次，2号开关被按了2次，3号开关被按了2次，4号开关被按了3次，5号开关被按了2次，6号开关被按了4次，7号开关被按了2次，8号开关被按了4次，9号开关被按了3次，…，
∴n号开关被按的次数等于n的约数的个数，
∴约数个数是奇数，则n一定是平方数．
∵100＝102，
∴100以内共有10个平方数，
∴最终状态为“亮”的灯共有10盏．
故答案为：10．
五．规律型：图形的变化类（共1小题）
5．（2023•十堰）用火柴棍拼成如图图案，其中第①个图案由4个小等边三角形围成1个小菱形，第②个图案由6个小等边三角形围成2个小菱形，…，若按此规律拼下去，则第n个图案需要火柴棍的根数为 6n+6 ．（用含n的式子表示）
【答案】6n+6．
【解答】解：∵第①个图案所需要的火柴棍的根数为：12＝3×4，
第②个图案所需要的火柴棍的根数为：18＝3×6，
第③个图案所需要的火柴棍的根数为：24＝3×8，
…，
∴第n个图案需要火柴棍的根数为：3（2n+2）＝6n+6．
故答案为：6n+6．
六．因式分解的应用（共1小题）
6．（2023•十堰）若x+y＝3，xy＝2，则x2y+xy2的值是 6 ．
【答案】6
【解答】解：∵x+y＝3，xy＝2，
∴x2y+xy2＝xy（x+y）＝2×3＝6，
故答案为：6．
七．反比例函数系数k的几何意义（共1小题）
7．（2023•湖北）在平面直角坐标系xOy中，若反比例函数y＝（k≠0）的图象经过点A（﹣1，﹣2）和点B（2，m），则△AOB的面积为 ．
【答案】．
【解答】解：∵反比例函数y＝的图象经过点A（﹣1，﹣2），
∴k＝（﹣1）×（﹣2）＝2，
∴反比例函数解析式为y＝，
∵反比例函数y＝的图象经过点B（2，m），
∴m＝＝1，
∴B（2，1），
设直线AB与x轴交于C，解析式为y＝kx+b，
则，
解答，
∴直线AB的解析式为y＝x﹣1，
当y＝0时，x＝1，
∴C（1，0）
∴△AOB的面积＝×1×1+×1×2＝．
故答案为：．
八．反比例函数图象上点的坐标特征（共1小题）
8．（2023•襄阳）点A（1，y1），B（2，y2）都在反比例函数的图象上，则y1 ＞ y2．（填“＞”或“＜”）
【答案】＞．
【解答】解：∵点A（1，y1），B（2，y2）在反比例函数的第一象限图象上，y随x的增大而减小，
∴y1＞y2．
故答案为：＞．
九．反比例函数与一次函数的交点问题（共1小题）
9．（2023•荆州）如图，点A（2，2）在双曲线y＝（x＞0）上，将直线OA向上平移若干个单位长度交y轴于点B，交双曲线于点C．若BC＝2，则点C的坐标是 （，2） ．
【答案】（，2）．
【解答】解：∵点A（2，2）在双曲线y＝（x＞0）上，
∴2＝．
∴k＝4．
∴双曲线解析式为y＝．
如图，作AD⊥x轴，CH⊥x轴，作BG⊥CH，垂足分别为D、H、G．
∵A（2，2），
∴AD＝OD．
∴∠AOD＝45°．
∴∠AOB＝45°．
∵OA∥BC，
∴∠CBO＝180°﹣45°＝135°．
∴∠CBG＝135°﹣90°＝45°．
∴∠CBG＝∠BCG．
∵BC＝2，
∴BG＝CG＝．
∴C点的横坐标为．
又C在双曲线y＝上，
∴C（，2）．
故答案为：（，2）．
一十．三角形内角和定理（共1小题）
10．（2023•十堰）一副三角板按如图所示放置，点A在DE上，点F在BC上，若∠EAB＝35°，则∠DFC＝ 100° ．
【答案】100°．
【解答】解：如图，
由题意得：∠BAC＝60°，∠C＝30°，∠D＝45°，
∵∠EAB＝35°，
∴∠CAD＝180°﹣∠EAB﹣∠BAC＝85°，
∴∠AGD＝180°﹣∠D﹣∠CAD＝50°，
∴∠CGF＝∠AGD＝50°，
∴∠DFC＝180°﹣∠C﹣∠CGF＝100°．
故答案为：100°．
一十一．菱形的性质（共1小题）
11．（2023•十堰）如图，在菱形ABCD中，点E，F，G，H分别是AB，BC，CD，AD上的点，且BE＝BF＝CG＝AH，若菱形的面积等于24，BD＝8，则EF+GH＝ 6 ．
【答案】6．
【解答】解：连接AC交BD于点O，
∵四边形ABCD是菱形，
∴AC⊥BD，AB＝BC＝CD＝AD，
∵菱形的面积等于24，BD＝8，
∴，
∴AC＝6，
∵BE＝BF，
∴∠BEF＝∠BFE＝180°﹣∠EBF，
∵BA＝BC，
∴∠BAC＝∠BCA＝180°﹣∠ABC，
∴∠BEF＝∠BAC，
∴EF∥AC，
∴△BEF∽△BAC，
∴，
∵BA＝DA，
∴，
同理可证△DHG∽△DAC，
∴，
∴，
即，
∴EF+GH＝AC＝6，
故答案为：6．
一十二．三角形的内切圆与内心（共1小题）
12．（2023•湖北）如图，在△ABC中，∠ACB＝70°，△ABC的内切圆⊙O与AB，BC分别相切于点D，E，连接DE，AO的延长线交DE于点F，则∠AFD＝ 35° ．
【答案】35°．
【解答】解：连接OD，OE，OB，OB交ED于点G，
∵∠ACB＝70°，
∴∠CAB+∠CBA＝110°，
∵点O为△ABC的内切圆的圆心，
∴∠OAB+∠OBA＝55°，
∴∠AOB＝125°，
∵OE＝OD，BD＝BE，
∴OB垂直平分DE，
∴∠OGE＝90°，
∴∠AFD＝∠AOB﹣∠OGF＝125°﹣90°＝35°，
故答案为：35°．
一十三．作图—基本作图（共1小题）
13．（2023•荆州）如图，∠AOB＝60°，点C在OB上，OC＝2，P为∠AOB内一点．根据图中尺规作图痕迹推断，点P到OA的距离为 1 ．
【答案】1
【解答】解：由作图知PE垂直平分OC，OP平分∠AOB，
∴OE＝OC＝，∠PEO＝90°，
∵∠AOB＝60°，
∴∠POE＝∠AOP＝＝30°，
∴EP＝OE×tan30°＝，
∵PO平分∠AOB，
∴点P到OA的距离＝PE＝1．
故答案为：1．
一十四．解直角三角形的应用（共1小题）
14．（2023•黄石）“神舟”十四号载人飞行任务是中国空间站建造阶段的首次载人飞行任务，也是空间站在轨建造以来情况最复杂、技术难度最高、航天员乘组工作量最大的一次载人飞行任务．如图，当“神舟”十四号运行到地球表面P点的正上方的F点处时，从点F能直接看到的地球表面最远的点记为Q点，已知PF＝km，∠FOQ＝20°，cs20°≈0.9，则圆心角∠POQ所对的弧长约为 π km（结果保留π）．
【答案】π．
【解答】解：设OP＝OQ＝rkm．
由题意，FQ是⊙O的切线，
∴FQ⊥OQ，
∵cs∠FOQ＝，
∴0.9＝，
∴r＝6400，
∴的长＝＝π（km）．
故答案为：π．
一十五．解直角三角形的应用-仰角俯角问题（共2小题）
15．（2023•湖北）综合实践课上，航模小组用航拍无人机进行测高实践．如图，无人机从地面CD的中点A处竖直上升30米到达B处，测得博雅楼顶部E的俯角为45°，尚美楼顶部F的俯角为30°，已知博雅楼高度CE为15米，则尚美楼高度DF为 （30﹣） 米．（结果保留根号）
【答案】（30﹣）
【解答】解：如图，过点E作EM⊥过点B的水平线于M，过点F作FN⊥过点B的水平线于N，
由题意可知CM＝DN＝AB＝30米，
又∵CE＝15米，
∴EM＝15米，
在Rt△EBM中，∠EBM＝45°，
∴BM＝EM＝15米，
又∵A是CD的中点，
∴BN＝AD＝AC＝BM＝15米，
在Rt△BFN中，tan∠FBN＝，
∵∠FBN＝30°，BN＝15米，
∴，
∴FN＝米，
∴DF＝（30﹣）米．
故答案为：（30﹣）．
16．（2023•黄石）如图，某飞机于空中A处探测到某地面目标在点B处，此时飞行高度AC＝1200米，从飞机上看到点B的俯角为37°，飞机保持飞行高度不变，且与地面目标分别在两条平行直线上同向运动．当飞机飞行943米到达点D时，地面目标此时运动到点E处，从点E看到点D的仰角为47.4°，则地面目标运动的距离BE约为 423 米．（参考数据：tan37°≈，tan47.4°≈）
【答案】423．
【解答】解：由题意得，∠C＝90°，∠ABC＝37°，AC＝1200米，
∴BC＝≈＝1600（米），
过D作DH⊥BC于H，
则四边形ACHD是矩形，
∴CH＝AD＝943米，DH＝AC＝1200米，
在Rt△DHE中，∠DHE＝90°，∠E＝47.4°，
∴＝1080（米），
∴BE＝CH+HE﹣BC＝943+1080﹣1600＝423（米），
答：地面目标运动的距离BE约为423米．
故答案为：423．
一十六．用样本估计总体（共1小题）
17．（2023•荆州）某校为了解学生对A，B，C，D四类运动的参与情况，随机调查了本校80名学生，让他们从中选择参与最多的一类，得到对应的人数分别是30，20，18，12．若该校有800名学生，则估计有 300 人参与A类运动最多．
【答案】300．
【解答】解：800×＝300（人）．
故估计有300人参与A类运动最多．
故答案为：300．
一十七．条形统计图（共1小题）
18．（2023•宜昌）如图，条形图描述了某车间工人日加工零件数的情况．这些工人日加工零件数的中位数是 6 ．
【答案】6．
【解答】解：由题意得，样本容量为：4+5+8+9+6+4＝36，
把这36个数从小到大排列，第18个与第19个都是6，因而中位数是6．
故答案为：6．
一十八．中位数（共1小题）
19．（2023•湖北）眼睛是心灵的窗户，为保护学生视力，启航中学每学期给学生检查视力，下表是该校某班39名学生右眼视力的检查结果，这组视力数据中，中位数是 4.6 ．
【答案】4.6．
【解答】解：将这组数据从小到大的顺序排列后，位于最中间的一个数是4.6，
所以中位数是4.6．
故答案为：4.6．
一十九．众数（共1小题）
20．（2023•鄂州）为了加强中学生“五项管理”，葛洪学校就“作业管理”、“睡眠管理”、“手机管理”、“读物管理”、“体质管理”五个方面对各班进行考核打分（各项满分均为100），九（1）班的五项得分依次为95，90，85，90，92，则这组数据的众数是 90 ．
【答案】90．
【解答】解：在数据95，90，85，90，92中，90出现了2次，出现的次数最多，
则这组数据的众数为90．
故答案为：90．视力
4.0
4.1
4.2
4.3
4.4
4.5
4.6
4.7
4.8
4.9
5.0
人数
1
2
6
3
3
4
1
2
5
7
5
视力
4.0
4.1
4.2
4.3
4.4
4.5
4.6
4.7
4.8
4.9
5.0
人数
1
2
6
3
3
4
1
2
5
7
5