6.2.4 用去分母法解一元一次方程 华东师大版七年级数学下册授课课件

这是一份6.2.4 用去分母法解一元一次方程 华东师大版七年级数学下册授课课件，共19页。

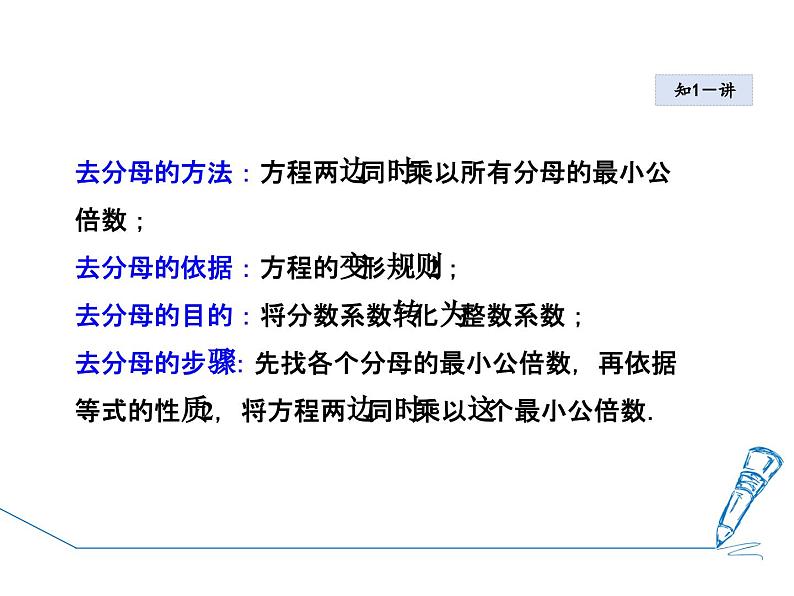
6.2 解一元一次方程第6章 一元一次方程第4课时 用去分母法解一元一次方程1课堂讲解去分母用去分母法解一元一次方程2课时流程逐点导讲练课堂小结作业提升小红有多少块糖？ 小红上幼儿园，“六·一”这天老师给了小红一些糖，回家后，小红先拿出糖的一半自己留给自己，然后把剩余的糖给爷爷一块，再把余下的糖的一半分给哥哥，又把给哥哥后剩余部分中那一块给妈妈，此时小红分完了所有的糖，原来小红有多少块糖呢？1知识点问题1 你能解右面的方程吗？知1－讲去分母能，学生会作如下解答：解：去括号，得　 移项得，得　 合并同类项，得 两边同除以 得　x＝－ 28答：知1－讲问题2 该方程与前两节课解过的方程有什么不同？以前学过的方程的系数都为整数，而这一题出现了分数.答：问题3 这个方程与前边的方程相比较，你喜欢解哪一种呢？解答前边的.答：问题4 能否把分数系数化为整数，把方程转化成我们以前学过的方程呢？可以. 在方程左边乘以7的倍数，右边乘以4的倍数，就可以去掉分母，把分数化为整数，所以我们可以根据等式性质2，在方程两边同时乘上一个既是7又是4的倍数28即可.答：知1－讲去分母的方法：方程两边同时乘以所有分母的最小公倍数；去分母的依据：方程的变形规则2；去分母的目的：将分数系数转化为整数系数；去分母的步骤：先找各个分母的最小公倍数，再依据等式的性质2，将方程两边同时乘以这个最小公倍数．例1 把方程 去分母，正确的是(　　)A．18x＋2(2x－1)＝18－3(x＋1)　B．3x＋2(2x－1)＝3－3(x＋1)C．18x＋(2x－1)＝18－(x＋1) D．18x＋4x－1＝18－3x＋1知1－讲导引：此方程所有分母的最小公倍数为6，方程两边都乘6，得18x＋2(2x－1)＝18－3(x＋1)，故选A.A知1－讲 B选项去分母时漏乘不含分母的项；C选项误认为含分母项最小公倍数都约去了；D选项忽略了分数线的括号作用；这三种情况恰是去分母常常易出现的错误，因此我们务必高度警惕．知1－练1　方程 去分母得（ ）A．2－2 (2x－4)= －（x－7） B．12－2 (2x－4)= －x－7C．12－2 (2x－4)= －（x－7） D．12－(2x－4)= －（x－7）2　将方程　　　　　　的两边同乘________可得到3(x＋2)＝2(2x＋3)，这种变形叫________，其依据是____________________．知1－练3　解方程　　　　　　　　时，为了去分母应将方程两边同乘(　　)A．10　　　　B．12　　　　C．24　　　　D．62知识点用去分母法解一元一次方程知2－讲问题1：去分母时，方程两边同乘以一个什么数合适呢？问题2：像方程 分子是多项式，去分母时应该如何处理？知2－讲 在方程的两边同乘以分母的最小公倍数时，不要漏乘常数项，在去分母时，要防止忽略分数线的括号作用，去分母时，如果分子是多项式的应该加括号.例2解方程： 知2－讲分析：这个方程中的系数出现了分数，通常可以将方程的两边都乘以同一个数（这里是都乘以6)，去掉方 程中的分母.像这样的变形通常称为“去分母”.解：去分母，得 3(x－3)－2(2x＋1)＝6，即 3x－9－4x－2＝6.移项，得 3x－4x＝6＋9＋2，即 －x＝7.两边都乘以(－1)，得 x＝－17.知2－讲 解含分母的一元一次方程的关键是去分母，而去分母的关键是找各个分母的最小公倍数，去分母的方法是将方程两边乘这个最小公倍数，解这类方程一般要经历：去分母→去括号→移项→合并同类项→系数化为1这五步．知2－练1　解方程：2　在解方程 的过程中：①去分母，得6－10x－1＝2(2x＋1)；②去括号，得6－10x－1＝4x＋2；③移项，得－10x－4x＝2－6－1；④合并同类项，得－14x＝－5；⑤系数化为1，得x＝ .其中开始出现错误的步骤是________．(填序号)例3解方程： 知2－讲导引：本例与上例的区别在于分母中含有小数，因此只要将分母的小数转化为整数就可按上例的方法来解了．解：根据分数的基本性质，得去分母，得　3x－(x－1)＝6x－2.去括号，得　3x－x＋1＝6x－2.移项，得　3x－x－6x＝－2－1.合并同类项，得－4x＝－3.系数化为1，得x＝知2－讲 本例解法体现了转化思想，即将分母中含有小数的方程运用分数的基本性质转化为分母为整数的方程，从而运用分母为整数的方程的解法来解；这里要注意运用分数的基本性质与运用等式的性质2的区别：前者是同一个分数的分子、分母同时乘一个数；后者是方程里各项同时乘一个数．知2－练1　解方程：2　下面是解方程 的过程，请在前面的括号内填写变形步骤，在后面的括号内填写变形依据．解：原方程可变形为 (　　)去分母，得3(3x＋5)＝2(2x－1)．(　　　　)去括号，得9x＋15＝4x－2.(　　　　)(　　　　)，得9x－4x＝－15－2.(　　　　)(　　　　)，得5x＝－17.(　　　　)，得x＝ (　　　　)1．解含分母的一元一次方程的关键是去分母，而去分母的关键是找各个分母的最小公倍数．2．运用分数的基本性质与运用等式的性质2的区别：前者是同一个分数的分子、分母同时乘一个数；后者是方程里各项同时乘一个数．3．用去分母法解一元一次方程要做到“三注意”：(1)去分母时，分子如果是一个多项式，要将分子作为一个整体加上括号．(2)去分母时，不含分母的项不要漏乘各分母的最小公倍数．(3)去括号时，不要出现漏乘现象和符号错误．