

浙江省宁波市镇海区镇海蛟川书院2023-2024学年八年级上学期期末数学试题(无答案)
展开(满分120分,考试时间120分钟)
一、选择题(共10小题,每小题3分,共30分)
1.宁波以“书藏古今,港通天下”闻名中外,以下这些属于宁波的Citywalk打卡点宣传图中,属于轴对称图形的是( )
A.B.
C.D.
2.使有意义的的取值范围是( )
A.B.C.D.
3.下列方程是一元二次方程的是( )
A.B.C.D.
4.下列命题是假命题的是( )
A.对顶角相等B.若,则
C.全等三角形对应角相等D.若,则
5.已知一次函数随的增大而增大,则该函数图象不经过第( )象限.
A.一B.二C.三D.四
6.已知关于的不等式的解集为,则的取值范围是( )
A.B.C.D.
7.如图,在平面直角坐标系中,点A的坐标是(0,2),以OA为边在y轴右侧作等边△OAA1,过点A1作x轴的垂线,垂足为O1,以O1A1为边在右侧作等边△O1A1A2,再过点A2作x轴的垂线,垂足为O2,以O2A2为边在右侧作等边△O2A2A3……按此规律继续作下去,则点A2024的纵坐标为( )
A.B.C.D.
8.新定义:《a,b,c》为一元二次方程(其中为实数)的“共同体数”,如:的“共同体数”为《1,2,-1》,以下“共同体数”中能让一元二次方程有两个不相等的实数根的是( )
A.《3,2,1》B.《3,4,5》C.《n+1,2n,n-1》D.
9.将两个直角三角形摆放如图,其中,则AD长为( )
(第9题图)
A.B.C.D.
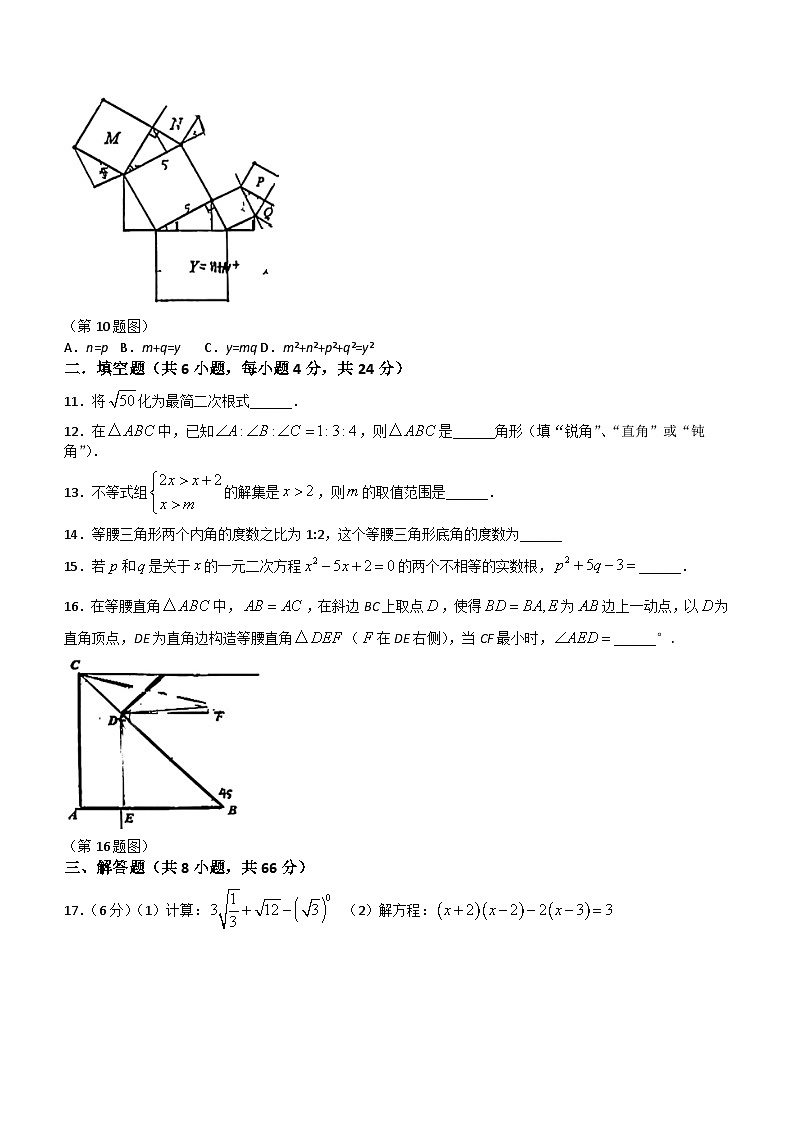
10.勾股定理被称为“几何学的基石”,以正方形一边为斜边向外作直角三角形,再以该直角三角形的两直角边为边长,分别向外作出正方形,重复这一过程就可以得到“勾股树”.如图,设大正方形Y的边长为定值y,四个小正方形MNPQ的边长分别为m,n,p,q,且三个直角三角形中,当变化时,以下说法错误的是( )
(第10题图)
A.n=pB.m+q=yC.y=mqD.m2+n2+p2+q2=y2
二.填空题(共6小题,每小题4分,共24分)
11.将化为最简二次根式______.
12.在中,已知,则是______角形(填“锐角”、“直角”或“钝角”).
13.不等式组的解集是,则的取值范围是______.
14.等腰三角形两个内角的度数之比为1:2,这个等腰三角形底角的度数为______
15.若和是关于的一元二次方程的两个不相等的实数根,______.
16.在等腰直角中,,在斜边BC上取点,使得为边上一动点,以为直角顶点,DE为直角边构造等腰直角(在DE右侧),当CF最小时,______°.
(第16题图)
三、解答题(共8小题,共66分)
17.(6分)(1)计算:(2)解方程:
18.(6分)解不等式组,并在数轴上表示此不等式组的解集.
19.(8分)如图,直线的解析表达式为:,且直线与轴交于点,直线经过点和,直线交于点.
(1)求点D的坐标;
(2)求直线l2的解析表达式;
(3)若直线l2上存在异于点C的另一点P,使得△ADP与△ADC的面积相等,请直接写出点P的坐标.
20.(8分)学校想了解初二年级学生对“二十大”知识的了解情况,进行了“二十大”知识竞赛测试,从801、802两个班中各随机抽取了10名学生的成绩,整理如下:(成绩得分用x表示,共分成四组:A.,B.,C.,D.)
801班10名学生的成绩是:96,80,96,86,99,98,92,100,89,82.
802班10名学生的成绩在C组中的数据是:94,90,92.
通过数据分析,列表如表:
801班、802班抽取的学生竞赛成绩统计表
802班学生成绩扇形统计图
根据以上信息,解答下列问题:
(1)直接写出上述a、b、c的值:a=______,b=______,c=______.
(2)学校欲选成绩更稳定的班级参加相关活动,根据表格中的数据,学校会选哪一个班级?说明理由.
(3)这两个班共100人参加了此次调查活动,估计两班参加此次调查活动成绩优秀()的学生总人数是多少?
21.(8分)如图①、图②、图③均是5×5的正方形网格,每个小正方形的边长都为1,每个小正方形的顶点称为格点,点A均为格点,只用无刻度的直尺按下列要求在给定的网格中画图,所画图形的顶点均在格点上,不要求写画法.
(1)在图①中找一格点B,连结AB,使线段.
(2)在图②中画出等腰△ABC,点B、C在格点上,使∠A为顶角且S△ABC=2.
(3)在图③中画出等腰△ABC,点B、C在格点上,使∠A为顶角且腰长为5.
图① 图② 图③
22.(8分)眼下,短视频和直播成为激发读者阅读兴趣并购书的新路径,促成作者与读者“双向奔赴”.某主播用双语直播带货图书《水浒传》,点燃了不同年龄者的读书热情.已知这本书的成本价为10元,规定销售单价不低于成本价,且不高于成本价的3倍,通过前几天的销售发现,该书每天的销售量(本)与销售单价x(元/本)之间近似满足一次函数关系,部分对应数据如表:
(1)根据表格提供的数据,求y关于x的函数关系式,并写出x的取值范围.
(2)若销售该书每天的利润为6000元,求该书的销售单价.
(3)销售该书每天的利润能否达到9000元?请说明理由.
23.(10分)【课本巩固】如图①,在等边△ABC中,D为边AB上一点,E为BC上一点,且AD=BE,连接AE与CD相交于点F.
(1)AE与CD的数量关系为______,AE与CD构成的锐角夹角∠CFE的度数是______;
【探究发现】
(2)在(1)的基础上,延长AE至点G,使FG=FC,连接BG,CG,如图②所示,求证:GA平分∠BGC.
【拓展延伸】
(3)如图③,在等边△ABC中,D为边AB上一点,E为BC上一点,且AD=BE,CF=3AF,CE=3BE,求.
图① 图② 图③
24.(12分)在平面直角坐标系中,A(-5,0),B(0,5).
(1)如图①,若C(3,0),过点A作AH⊥BC交y轴于点D,求点D的坐标;
(2)如图②,若点C在x轴正半轴上运动,且OC<5,过点A作AH⊥BC交y轴于点D,连接OH,当OC+CH=AH时,求∠OBC的度数.
(3)如图③,若C是线段AB上的一个动点,点P在△ABO内部,BP=4,OP=3,连结CP,设BC=a,求△BPC的面积S关于a的解析式.
图① 图② 图③
年级
平均数
中位数
众数
方差
801班
92
b
c
52
802班
92
94
100
50.4
x(元/本)
…
15
25
…
(本)
…
700
500
…
浙江省宁波市镇海区镇海蛟川书院2023-2024学年八年级上学期期末数学试题: 这是一份浙江省宁波市镇海区镇海蛟川书院2023-2024学年八年级上学期期末数学试题,共6页。试卷主要包含了选择题,解答题等内容,欢迎下载使用。
90,浙江省宁波市镇海区镇海蛟川书院2023-2024学年九年级上学期期末数学试题: 这是一份90,浙江省宁波市镇海区镇海蛟川书院2023-2024学年九年级上学期期末数学试题,共22页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
浙江省宁波市镇海区镇海蛟川书院2023-2024学年九年级上学期期末数学试题: 这是一份浙江省宁波市镇海区镇海蛟川书院2023-2024学年九年级上学期期末数学试题,共4页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。












