数学北师6（下）整理与复习 整理与复习（1） 课件

这是一份数学北师6（下）整理与复习 整理与复习（1） 课件，共31页。

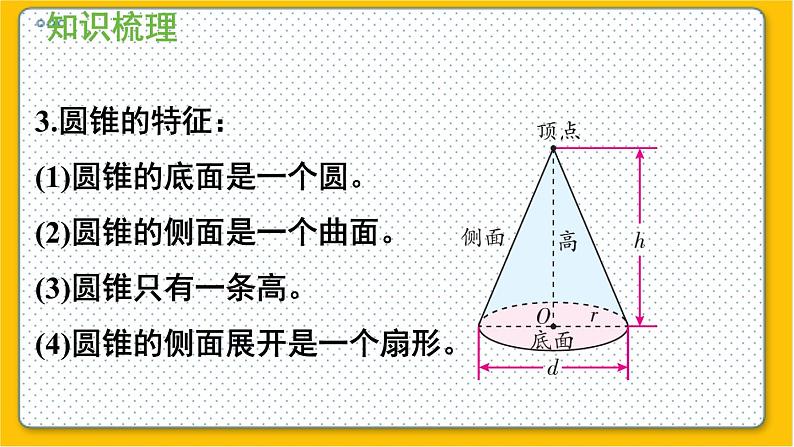
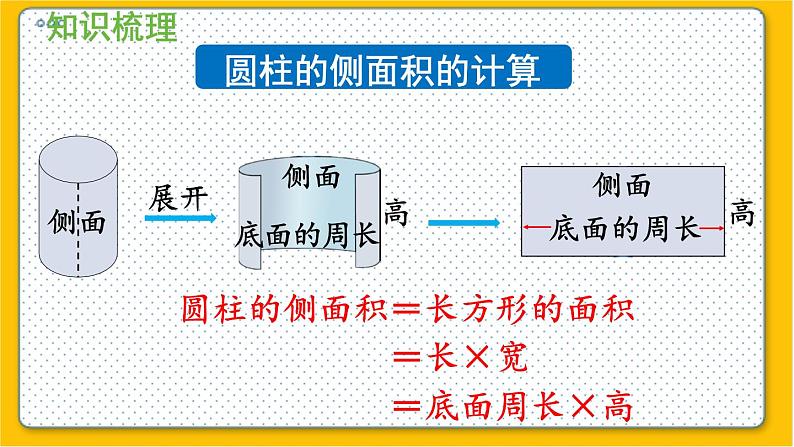
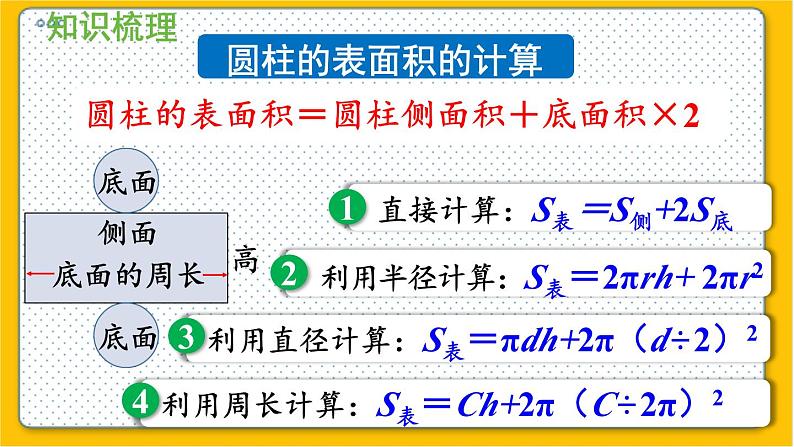
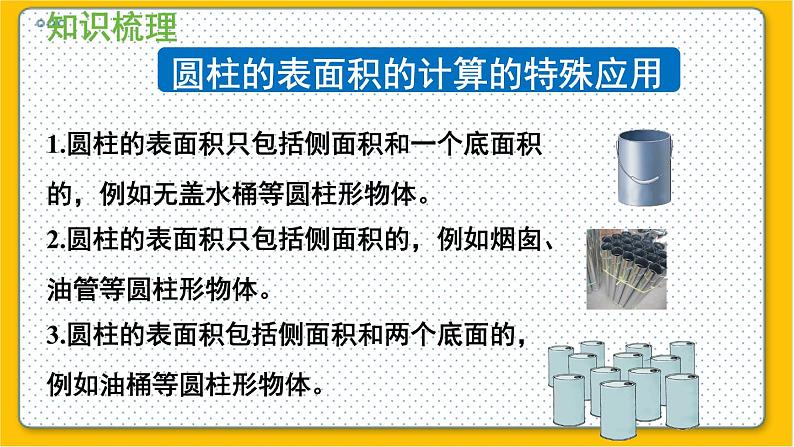
整理与复习（1）1.“点、线、面、体”之间的关系是：点的运动形成线；线的运动形成面；面的旋转形成体。2.圆柱的特征：(1)圆柱的两个底面是半径相等的两个圆。(2)两个底面间的距离叫作圆柱的高。(3)圆柱有无数条高，且高的长度都相等。(4)圆柱的侧面是个曲面，沿高剪开，展开后是一个长方形，长方形的长是圆柱的底面周长，长方形的宽是圆柱的高。3.圆锥的特征：(1)圆锥的底面是一个圆。(2)圆锥的侧面是一个曲面。(3)圆锥只有一条高。(4)圆锥的侧面展开是一个扇形。圆柱的侧面积的计算＝底面周长×高＝长×宽圆柱的侧面积＝长方形的面积展开侧面底面的周长高高侧面侧面圆柱的侧面积的计算圆柱的侧面积＝圆柱的底面周长×高圆柱的表面积的计算圆柱的表面积＝圆柱侧面积＋底面积×21.圆柱的表面积只包括侧面积和一个底面积的，例如无盖水桶等圆柱形物体。2.圆柱的表面积只包括侧面积的，例如烟囱、油管等圆柱形物体。3.圆柱的表面积包括侧面积和两个底面的，例如油桶等圆柱形物体。圆柱的表面积的计算的特殊应用圆柱体积的计算圆柱的体积＝圆柱的底面积×高圆锥体积的计算  圆锥体积的计算 我会填空。1.一个圆柱体的侧面沿侧面的一条高展开后是( )，当( )和( )相等的时候是( )。它的长等于圆柱的( )，宽等于圆柱的( )，所以圆柱的侧面积 =( )×( )。2.圆柱体( )叫圆柱体的高。一个圆柱体有( )条高，一个圆锥体只有( )条高。长方形　高　底面周长　正方形底面周长　高底面周长　高　两个底面之间的距离无数一1.（1）一个圆柱体状的杯子的体积就是它的容积。 ( )　（2）若两个圆柱体的侧面积相等，则它们的体积也相等。 ( )　（3）以三角形的一条边为轴旋转一周一定可以得到一个圆锥体。 ( )　（4）如果一个物体上下两个底是相同的圆，侧面是曲面，则这个物体一定是圆柱体。　(　　　)　（5）圆柱的体积等于圆锥体积的3倍。　(　　　)　×××××2.我会判断。(对的画“√”，错的画“×”）（1）在长4米的圆柱形钢柱上，用一根长31.4分米的铁丝正好沿钢柱绕10圈，这根钢柱的体积是( )立方分米。 A. 31.4 B. 125.6 C. 31400　（2）把一个大圆柱分成两个小圆柱后发生变化的是( )　 A.圆柱的体积 B.圆柱的表面积 C.圆柱的侧面积　AB3.我会选择。(将正确的答案的序号填入括号里) 25.12+3.14×2²×2=25.12+25.12=50.24（平方厘米）一个圆柱的侧面积是25.12平方厘米，底面半径是2厘米，求该圆柱的表面积是多少？ 答：圆柱的表面积是50.24平方厘米。4.一座大厦有四根同样的圆柱，已知圆柱的底面周长是15.7dm，高10m，如果要把圆柱的侧面都包裹上彩布，至少需彩布多少平方分米 ?  10m=100dm 15.7×100×4=1570×4=6280（平方分米）答：至少需彩布6280平方分米。5.一个圆柱，表面积是345.4平方厘米，底半径是5厘米，求它的高。底面积： 3.14×5²×2=78.5×2=157（平方厘米）答：它的高是6厘米。侧面积： 345.4-157=188.4（平方厘米）高： 188.4÷31.4=6（厘米）底面周长： 3.14×5×2=15.7×2=31.4（厘米）6.把一长为1.6米的圆柱截成3段后，表面积增加了9.6平方米，求圆柱原来的体积？ 9.6÷4×1.6=2.4×1.6=3.84（立方米）答：圆柱原来的体积是3.84立方米。7.把长为20分米的圆柱沿着底面直径劈开，表面积增加了80平方分米，求该圆柱原来的表面积是多少？底面积： 3.14×（2÷2）²×2=3.14×2=6.28（平方分米）答：圆柱原来的表面积是131.88平方分米。直径： 80÷2÷20=40÷20=2（分米）侧面积： 3.14×2×20=6.28×20=125.6（平方分米）表面积： 6.28+125.6=131.88（平方分米）8.一个圆柱容器半径是5分米，把一铁块拿出后，水面下降3分米，求铁块体积。 3.14×5²×3=78.5×3=235.5（立方分米）答：铁块体积是235.5立方米。9.用一张长8厘米，宽6厘米的长方形，以长为轴旋转成圆柱，求圆柱的体积。 3.14×6²×8=113.04×8=904.32（立方厘米）答：圆柱的体积是904.32立方厘米。10.用一个两条直角边分别为8厘米、6厘米的直角三角形，以长直角边为轴旋转成圆锥，求圆锥的体积。 答：圆锥的体积是301.44立方厘米。11.上面一排图形旋转后会得到下面的哪个图形？ 想一想， 连一连。1.60π68π60π20π240π312π720π240π填表。2.一个圆锥形谷堆， 底面直径为 6 m， 高 1.2 m。（1） 这堆稻谷的体积是多少立方米？ 答：这堆稻谷的体积是11.304立方米。3.一个圆锥形谷堆， 底面直径为 6 m， 高 1.2 m。（2）如果每立方米稻谷的质量为 700 kg， 这堆稻谷的质量为多少千克？11.304×700=7912.8（千克）答：这堆稻谷的质量是7912.8千克。3.用白铁皮制作圆柱形通风管，每节长80 cm，底面半径5cm，制作20节这样的通风管， 至少需用多大面积的铁皮？　 3.14×5×2×80×20=31.4×80×20=2512×20=50240（平方厘米）答：一共要用50240平方厘米的铁皮。4.用铁皮制作一个有盖的圆柱形油桶，底面半径是3dm，高与底面半径的比是2:1。（1）制作这个油桶至少需要多少平方分米的铁皮？3×2=6（dm）2×3.14×3×63.14×32×2=169.56（dm2）答：制作这个油桶至少需要169.56平方分米的铁皮。+5.用铁皮制作一个有盖的圆柱形油桶，底面半径是3dm，高与底面半径的比是2:1。（2）这个油桶的容积是多少升？5.3.14×32×6=169.56（dm3）=169.56（L）答：这个油桶的容积是169.56升。如图是我国古代的一种计量时间的仪器沙漏（又称沙钟），它分上下两部分，是根据流沙从上面的容器漏到下面的容器的数量来计量时间的。（单位：cm）（1）这时沙漏上部剩余的沙子的体积是多少立方厘米？答：这时沙漏上部剩余的沙子的体积是3.14立方厘米。6.3.14（cm3 ）如图是我国古代的一种计量时间的仪器沙漏（又称沙钟），它分上下两部分，是根据流沙从上面的容器漏到下面的容器的数量来计量时间的。（单位：cm）（2）这时沙漏下部沙子的体积是多少立方厘米？答：这时沙漏下部沙子的体积是74.1825立方厘米。6.84.78（cm3 ）10.5975（cm3 ）84.78－10.5975=74.1825（cm3 ）