专题23 与垂径定理有关的拓展探究-【微专题】2022-2023学年九年级数学上册常考点微专题提分精练（人教版）

这是一份专题23 与垂径定理有关的拓展探究-【微专题】2022-2023学年九年级数学上册常考点微专题提分精练（人教版），文件包含专题23与垂径定理有关的拓展探究原卷版docx、专题23与垂径定理有关的拓展探究解析版docx等2份试卷配套教学资源，其中试卷共46页， 欢迎下载使用。
1．问题提出
（1）如图①，的半径为8，弦，则点O到的距离是__________．
问题探究
（2）如图②，的半径为5，点A、B、C都在上，，求面积的最大值．
问题解决
（3）如图③，是一圆形景观区示意图，的直径为，等腰直角三角形的边是的弦，直角顶点P在内，延长交于点C，延长交于点D，连接．现准备在和区域内种植草坪，在和区域内种植花卉．记和的面积和为，和的面积和为．
①求种植草坪的区域面积．
②求种植花卉的区域面积的最大值．
2．问题提出：（1）如图1，已知是边长为2的等边三角形，则的面积为______．
问题探究：（2）如图2，在中，已知，，求的最大面积．
问题解决：（3）如图3，某校学生礼堂的平面示意图为矩形ABCD，其宽米，长米，为了能够监控到礼堂内部情况，现需要在礼堂最尾端墙面CD上安装一台摄像头M进行观测，并且要求能观测到礼堂前端墙面AB区域，同时为了观测效果达到最佳，还需要从点M出发的观测角．请你通过所学的知识进行分析，在墙面CD区域上是否存在点M满足要求？若存在，求出MC的长度；若不存在，请说明理由．

3．【学习心得】
（1）小雯同学在学习完“圆”这一章内容后，感觉到一些几何问题如果添加辅助圆，运用圆的知识解决，可以使问题变得非常容易．
例如：如图，在中，，，D是外一点，且，求的度数．若以点A为圆心，AB长为半径作辅助圆，则C，D两点必在上，是的圆心角，是的圆周角，则______°．
【初步运用】
（2）如图，在四边形ABCD中，，，求的度数；
【方法迁移】
（3）如图，已知线段AB和直线l，用直尺和圆规在l上作出所有的点P，使得（不写作法，保留作图痕迹）；
【问题拓展】
（4）①如图，已知矩形ABCD，，，M为边CD上的点．若满足的点M恰好有两个，则m的取值范围为______．
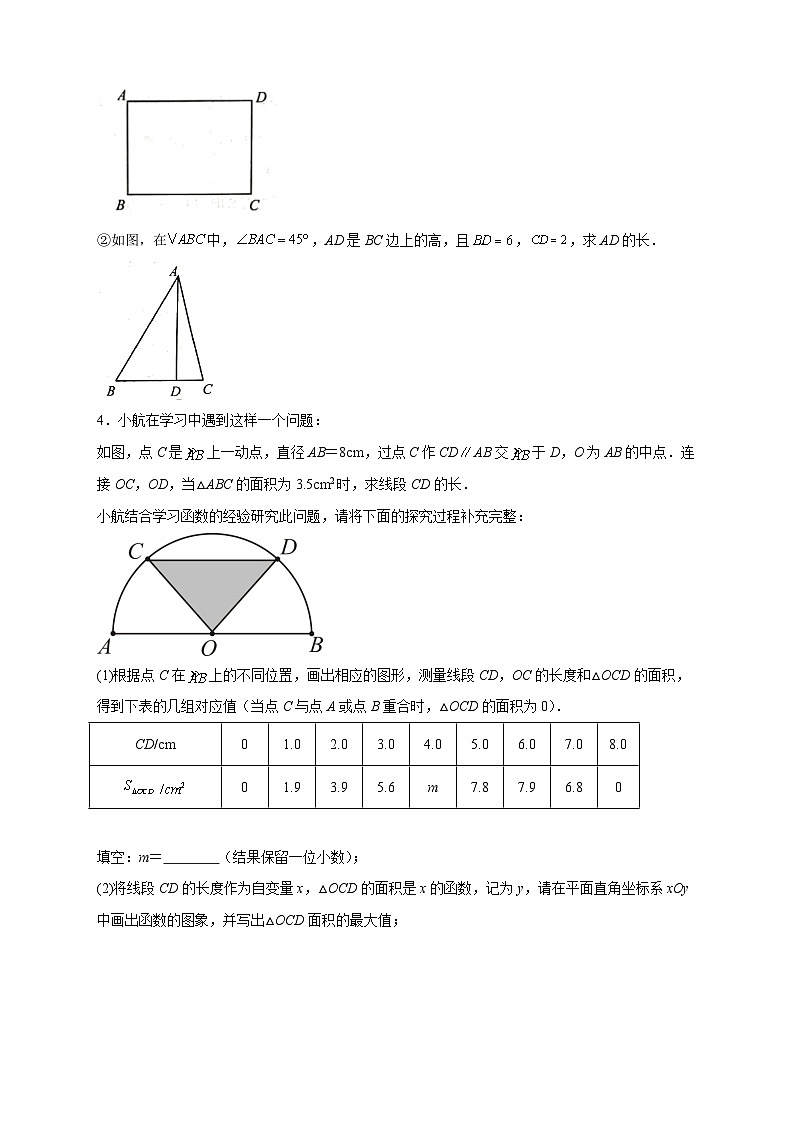
②如图，在中，，AD是BC边上的高，且，，求AD的长．
4．小航在学习中遇到这样一个问题：
如图，点C是上一动点，直径AB＝8cm，过点C作CDAB交于D，O为AB的中点．连接OC，OD，当△ABC的面积为3.5cm2时，求线段CD的长．
小航结合学习函数的经验研究此问题，请将下面的探究过程补充完整：
(1)根据点C在上的不同位置，画出相应的图形，测量线段CD，OC的长度和△OCD的面积，得到下表的几组对应值（当点C与点A或点B重合时，△OCD的面积为0）．
填空：m＝ （结果保留一位小数）；
(2)将线段CD的长度作为自变量x，△OCD的面积是x的函数，记为y，请在平面直角坐标系xOy中画出函数的图象，并写出△OCD面积的最大值；
(3)在同一坐标系中画出所需的图象，并结合图象直接写出：当△OCD的面积为3.5cm2时，线段CD长度的近似值（结果保留一位小数）．
5．【教材回顾】（1）如图①，点、分别是的边、边的中点，连结，则是的一条中位线．则和的数量关系是____，位置关系是_____．
【提出问题】如图④，是以为直径的⊙的一条弦，连结、，点在的上方，点在的下方，于，于，点、均在弦上．已知，，求的值．为了解决上面的问题，进行了如下的探究：
【分析问题】先看两种特殊情况：
（2）如图②，当点与点重合时，点也与点重合，点与点重合，此时，（点看成是长度为0的线段），则_____．（写出具体的数值）
（3）如图③，当时，、重合，此时与的数量关系是____，先根据条件易求的长度，则____．（写出具体的数值）
【解决问题】（4）结合图④对应的一般情况和你的感知，请用严谨的数学方法求的值．
6．学习心得：小刚同学在学习完“圆”这一章内容后，感觉到一些几何问题，如果添加辅助圆，运用圆的知识解决，可以使问题变得非常容易．例如：已知，如图1，在ABC中，AB＝AC，∠BAC＝90°，D是ABC外一点，且AD＝AC，求∠BDC的度数．若以点A为圆心，AB为半径作辅助圆⊙A，则点C、D必在⊙A上，∠BAC是⊙A的圆心角，而∠BDC是圆周角，从而可容易得到∠BDC＝ ．（直接写答案）
问题解决：如图2，在四边形ABCD中，∠BAD＝∠BCD＝90°，∠BDC＝25°，求∠BAC的度数；
问题拓展：如图3，在ABC中，∠BAC＝45°，AD是BC边上的高，且BD＝4，CD＝2，求AD的长．
7．小航在学习中遇到这样一个问题：
小航结合学习函数的经验研究此问题，请将下面的探究过程补充完整：
（1）根据点在线段上的不同位置，画出相应的图形，测量线段，，的长度，得到下表的几组对应值．
填空：的值为_________，的值为___________；
（2）将线段的长度作为自变量，和的长度都是的函数，分别记为和，并在平面直角坐标系中画出了函数的图象，如图所示．请在同一坐标系中画出函数的图象；
（3）继续在同一坐标系中画出所需的函数图象，并结合图象直接写出：当为等腰三角形时，线段长度的近似值（结果保留一位小数）．
8．问题提出
（1）如图①，已知直线，点A，B在直线a上，点C，D在直线b上，则_______（填“＞”“＜”或“＝”）；
问题探究
（2）如图②，⊙O的直径为20，点A，B，C都在⊙O上，，求面积的最大值；
问题解决
（3）如图③，在中，，，，根据设计要求，点D为内部一点，且，过点C作交BD于点E，连接AE，CD，试求满足设计要求的四边形ADCE的最大面积．
9．【定义】圆心到弦的距离叫做弦心距．
【探究】等弧所对弦的弦心距相等．
（1）请在图1中画出图形，写出已知、求证并证明．
【应用】
（2）如图2，的弦，的延长线相交于点，且，连接．求证：平分．
10．[阅读材料]如图1所示，对于平面内⊙P，在⊙P上有弦AB，取弦AB的中点M，我们把弦AB的中点M到某点或某直线的距离叫做弦AB到这点或者这条直线的“密距”例如：图1中线段MO的长度即为弦AB到原点O的“密距”，过点M作y轴的垂线交y轴于点N线段MN的长度即为弦AB到y轴的“密距”．
[类比应用]
已知⊙P的圆心为P（0，4），半径为2，弦AB的长度为2，弦AB的中点为M．
（1）当AB//y轴时，如图2所示，圆心P到弦AB的中点M的距离是____，此时弦AB到原点O的“密距”是 ；
（2）①如果弦AB在⊙P上运动，在运动过程中，圆心P到弦AB的中点M的距离变化吗?若不变化，请求出PM的长，若变化，请说明理由．
②直接写出弦AB到原点O的“密距”d的取值范围 ；
[拓展应用]如图3所示，已知⊙P的圆心为P（0，4），半径为2,点A（0，2），点B为⊙P上白一动点，有直线y=-x-3，弦AB到直线y=-x-3的“密距”的最大值是 ．（直接写出答案）
11．问题提出（1）如图①，在△ABC中，BC＝6，D为BC上一点，AD＝4，则△ABC面积的最大值是 ．
问题探究（2）如图②，已知矩形ABCD的周长为12，求矩形ABCD面积的最大值．
问题解决（3）如图③，△ABC是葛叔叔家的菜地示意图，其中AB＝30米，BC＝40米，AC＝50米，现在他想利用周边地的情况，把原来的三角形地拓展成符合条件的面积尽可能大、周长尽可能长的四边形地，用来建鱼塘．已知葛叔叔欲建的鱼塘是四边形ABCD，且满足∠ADC＝60°．你认为葛叔叔的想法能否实现？若能，求出这个四边形鱼塘周长的最大值；若不能，请说明理由．
12．如图，⊙O的半径为1，A，P，B，C是⊙O上的四个点．∠APC=∠CPB=60°．
(1)试探究线段PA，PB，PC之间的数量关系，并证明你的结论；
(2)当点P位于什么位置时，四边形APBC的面积最大？求出最大面积．
13．如图，△ABC是圆内接等腰三角形，其中AB=AC，点P在上运动（点P与点A在弦BC的两侧），连结PA，PB，PC，设∠BAC=α，=y，小明为探究y随α的变化情况，经历了如下过程
（1）若点P在弧BC的中点处，α=60°时，y的值是______．
（2）小明探究α变化获得了一部分数据，请你填写表格中空缺的数据．在如图2平面直角坐标系中以表中各组对应值为点的坐标进行描点，并画出函数图象：
（3）从图象可知，y随着α的变化情况是______；y的取值范围是______．
CD/cm
0
1.0
2.0
3.0
4.0
5.0
6.0
7.0
8.0
0
1.9
3.9
5.6
m
7.8
7.9
6.8
0
如图，点是线段上一动点，线段，的垂直平分线交于，取线段的中点，连接并延长交于，连接．若是等腰三角形，求线段的长度．
/cm
0
1.0
2.0
3.0
4.0
5.0
6.0
7.0
8.0
/cm
6.7
5.6
4.5
3.5
3.5
4.5
6.7
/cm
6.7
6.5
6.2
5.7
5.0
4.2
3.6
3.2
2.9
α
…
30°
60°
90°
120°
150°
170°
…
y
．．
0.52
1.73
1.93
1.99
…