专题02 已知面积求k-【微专题】2022-2023学年九年级数学下册常考点微专题提分精练（人教版）

这是一份专题02 已知面积求k-【微专题】2022-2023学年九年级数学下册常考点微专题提分精练（人教版），文件包含专题02已知面积求k原卷版docx、专题02已知面积求k解析版docx等2份试卷配套教学资源，其中试卷共41页， 欢迎下载使用。

1．如图，点是函数图像上的任意一点，过点作ABx轴，交另一个函数的图像于点．
(1)若，则________．
(2)当时，若点的横坐标是1，则线段________．
(3)若无论点在何处，函数图像上总存在一点，使得四边形为平行四边形，求的值．
【答案】(1)－6
(2)
(3)存在，
【分析】（1）如图：AB交y轴于M，根据反比例函数的比例系数的几何意义得，，由于，则，即可得出k的值；
（2）由可得出，再由可得出，即可得出的长度；
（3）如图，作轴于点，于点，证，得出D点的坐标即可得出的值．
（1）
解：如图：AB交y轴于M，
∵点是函数，点是函数，
∴由反比例函数的比例系数的几何意义得：，,
∵,
∴,
∴；
故答案为：；
（2）
由题意得：
当时，，
∴，
当时，，
当时，，
∴，
∴，
∴；
故答案为：；
（3）
存在，点在点上方，
如图，作轴于点，于点，
设，则，则，，
∵四边形为平行四边形，
∴，，
∴，
∵轴，
∴，
∴，
∴，，
∴，
∴，
解得．
【点睛】本题考查了反比例函数的综合题：掌握反比例函数图像上点的坐标特征、反比例函数的比例系数的几何意义和平行四边形的性质是解题的关键．
2．如图，在平面直角坐标系中，O为坐标原点，Rt△OAB的直角边OB在x轴的正半轴上，点A的坐标为（6，4），斜边OA的中点D在反比例函数y（x＞0）的图象上，AB交该图象于点C，连接OC．
(1)求k的值；
(2)求△OAC的面积．
【答案】(1)6
(2)9
【分析】（1）根据线段中点的坐标的确定方法求得点的坐标，再根据反比例函数图象上点的坐标特征求出；
（2）由反比例函数解析式求出点的纵坐标，进而求出的长，再根据三角形的面积公式计算即可．
（1）解：点的坐标为，点为的中点，点的坐标为，点在反比例函数的图象上，；
（2）解：由题意得，点的横坐标为6，点的纵坐标为：，，的面积．
【点睛】本题考查的是反比例函数系数的几何意义、反比例函数图象上点的坐标特征，掌握反比例函数的性质、解题的关键是正确求出的长度．
3．如图，点A在反比例函数的图像上，轴，垂足为B，．
(1)求k的值：
(2)点C在这个反比例函数图像上，且，求OC的长．
【答案】(1)8
(2)
【分析】（1）利用正切函数的定义可求出OB的长度，进而根据反比例函数中k值的几何意义可求得k值．
（2）连接OC,过点C作轴于点H，过点A作于点M，根据（1）中结论利用矩形的性质可求出OH，CH的长度，进而利用勾股定理可得OC长度．
(1)
解：
根据k值的几何意义可知：
(2)
解：如图所示，连接OC,过点C作轴于点H，过点A作于点M．
四边形AMHB是矩形
设，则，
解得：（舍去）
则
【点睛】本题考查了反比例函数的几何应用，涉及到勾股定理、矩形的判定与性质、以及反比例函数的性质，熟练掌握反比例函数中的k值的几何意义是解决本题的关键．
4．如图，一次函数的图象分别交轴、轴于、，为上一点且为的中位线，的延长线交反比例函数（）的图象于点，．
（1）求点和点的坐标；
（2）求的值和点的坐标．
【答案】（1）A（4，0），B（0，-2）；（2），Q的坐标为(2 ，)．
【分析】（1）因为一次函数y=x-2的图象分别交x轴，y轴于A，B，所以当y=0时，可求出A的横坐标，当x=0时可求出B的纵坐标，从而可得解．
（2）因为三角形OQC的面积是Q点的横纵坐标乘积的一半，且等于，所以可求出k的值，PC为中位线，可求出C的横坐标，也是Q的横坐标，代入反比例函数可求出纵坐标．
【详解】解：（1）设A点的坐标为（a，0），B点坐标为（0，b），
分别代入y=x-2，解方程得a=4，b=-2，
∴A（4，0），B（0，-2）；
（2）∵PC是△AOB的中位线，
∴PC⊥x轴，即QC⊥OC，
又Q在反比例函数的图象上，
∴2S△OQC=k，
∴k=2×=3，
∵PC是△AOB的中位线，
∴C（2，0），
可设Q（2，q）
∵Q在反比例函数的图象上，
∴q=，
∴点Q的坐标为(2 ，)．
【点睛】本题考查反比例函数的综合运用，熟练掌握并应用反比例函数（）中k的几何意义是解题的关键．
5．已知反比例函数（k为常数，）．
（Ⅰ）若点在这个函数的图象上，求k的值；
（Ⅱ）若在这个函数图象的每一支上，y随x的增大而减小，求k的取值范围；
（Ⅲ）如图，若反比例函数的图象经过点A，轴于B，且的面积为6，求k的值；
【答案】（1）；（2）；（3）
【分析】（1）根据反比例函数图象上点的坐标特征得到k-1=1×2，然后解方程即可；
（2）根据反比例函数的性质得k-1>0，然后解不等式即可；
（3）根据反比例函数k的几何意义求解即可．
【详解】（1）∵点在这个函数的图象上，
∴，
∴；
（2）∵在这个函数图象的每一支上，y随x的增大而减小，
∴，
∴；
（3）由题根据反比函数k的几何意义，可知：，
∴，解得：或，
又∵反比例函数图象经过第二象限，
∴，即：，
∴．
【点睛】本题考查求解反比例函数的系数，反比函数的性质及反比例函数k的几何意义，熟记基本性质是解题关键．
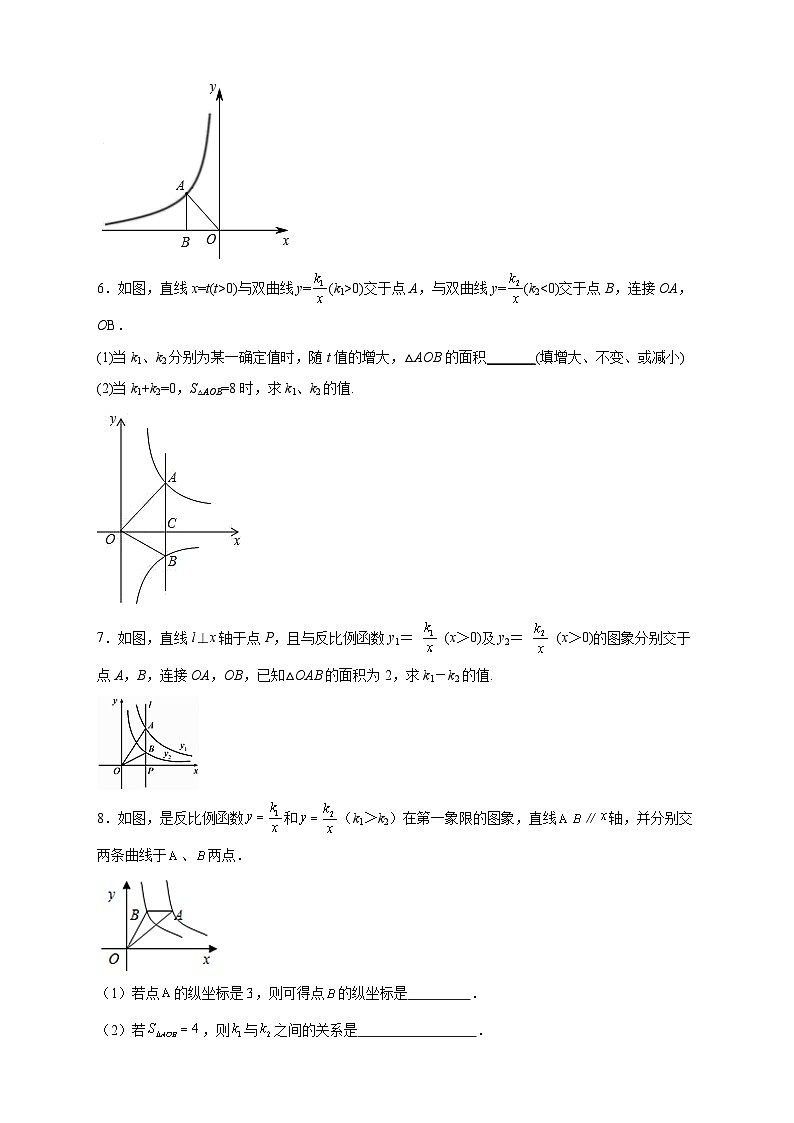
6．如图，直线x=t(t>0)与双曲线y=(k1>0)交于点A，与双曲线y=(k2<0)交于点B，连接OA，OB．
(1)当k1、k2分别为某一确定值时，随t值的增大，△AOB的面积_______(填增大、不变、或减小)
(2)当k1+k2=0，S△AOB=8时，求k1、k2的值.
【答案】（1）不变；（2）k1＝8，k2＝﹣8．
【分析】（1）根据反比例函数系数k的几何意义即可得出答案；
（2）由题意可知S△AOB＝k1﹣k2，然后与k1+k2＝0构成方程组，解之即可．
【详解】解：（1）不变.
∵S△AOC＝|k1|，S△BOC＝|k2|，
∴S△AOB＝S△AOC+S△BOC＝（|k1|+|k2|），
∵k1，k2分别为某一确定值，∴△AOB的面积不变.
故答案为：不变；
（2）由题意知：k1＞0，k2＜0，∴S△AOB＝k1﹣k2＝8，
∵k1+k2＝0，∴k1＝8，k2＝﹣8．
【点睛】本题考查的是反比例函数系数k的几何意义，属于常考题型，熟知反比例函数系数k的几何意义是解题的关键．
7．如图，直线l⊥x轴于点P，且与反比例函数y1＝ (x＞0)及y2＝ (x＞0)的图象分别交于点A，B，连接OA，OB，已知△OAB的面积为2，求k1－k2的值.
【答案】4
【分析】根据反比例函数k的几何意义可知：△OAP的面积为，△OBP的面积为，由题意可知△OAB的面积为即可得出答案
【详解】解：∵反比例函数 （x＞0）及 （x＞0）的图象均在第一象限内，∴ ＞0， ＞0
∵AP⊥x轴，∴S△OAP= ，S△OBP= ，∴S△OAB=S△OAP﹣S△OBP= =2，解得： =4
【点睛】本题考查了反比例k的几何意义，得出的关系是解题的关键
8．如图，是反比例函数和（k1＞k2）在第一象限的图象，直线∥轴，并分别交两条曲线于、两点．
（1）若点的纵坐标是，则可得点的纵坐标是 ．
（2）若，则与之间的关系是 ．
【答案】（1），（2）．
【详解】试题分析：（1）平行线间的距离处处相等，B到x轴的距离也是3．（2）由图像知与都大于0，延长AB交y轴于C,△AOC的面积等于二分之一乘以K1，△BOC的面积二分之一乘以K2，这两个三角形面积相减等于△AOB的面积=4，解得．
考点：反比例函数图像性质
9．如图，A、B是双曲线y(x＞0)上两点，A、B两点的横坐标分别为1、2，线段AB的延长线交x轴于点C，若△AOC的面积为6，求k的值．
【答案】4
【分析】作AD⊥x轴于D，BE⊥x轴于E，如图，根据反比例函数图象上点的坐标特征得到A(1,k)，B(2,)，则OD=1，DE=1，AD=2BE，所以BE为△ADC的中位线，得到CE=DE=1，然后根据三角形面积公式计算k的值．
【详解】解：作AD⊥x轴于D，BE⊥x轴于E，如图，
∵A、B两点的横坐标分别为1、2，
∴A（1,k），B（2,），
∴OD＝1，DE＝1，AD＝2BE，
∴BE为△ADC的中位线，
∴CE＝DE＝1，
∴OC＝3，
∵△AOC的面积为6，
∴＝6，
∴k＝4．
【点睛】本题考查了比例系数k的几何意义：在反比例函数y=图象中任取一点，过这一个点向x轴和y轴分别作垂线，与坐标轴围成的矩形的面积是定值|k|．
10．如图，A、B是双曲线y＝上的两点，过A点作AC⊥x轴，交OB于D点，垂足为C，连接OA，过B点作BE⊥x轴，垂足为E．若△ADO的面积为1，D为OB的中点．
(1)四边形DCEB的面积为 ；
(2)求k的值；
(3)若A、B两点的横坐标恰好是方程x2﹣3x+2＝0的两个不同实根，求点E到直线OA的距离．
【答案】(1)1
(2)
(3)
【分析】（1）根据反比例函数k的几何意义得到△AOC与△BOE面积相等，进而得到四边形CDBE面积与△AOD面积相等，即可得到结果；
（2）证明△COD∽△EOB，根据D为OB中点，得到面积之比为1：4，求出△COD面积，得到△BOE面积，即可确定出k的值；
（3）先根据因式分解法解一元二次方程，确定点A的坐标，根据勾股定理可得OA的长，最后根据三角形面积公式可得结论．
（1）解：∵A、B是双曲线y＝上的两点，AC⊥x轴，BE⊥x轴，∴S△AOC＝S△BOE，即S△AOD+S△COD＝S△COD+S四边形CDBE，∵S△AOD＝1，∴S四边形CDBE＝S△AOD＝1，故答案为：1；
（2）解：∵AC⊥x轴，BE⊥x轴，∴AC∥BE，∴△COD∽△EOB，∵D为OB中点，∴C是OE的中点，∴CD＝BE，∴S△COD：S△BOE＝1：4，∴S△COD：S四边形CDBE＝1：3，∴S△DOC＝，∴S△BOE＝，∴k＝；
（3）解：∵x2﹣3x+2＝0，∴（x﹣1）（x﹣2）＝0，∴x1＝1，x2＝2，∴点A的横坐标为1，点B的横坐标为2，当x＝1时，y＝，∴A（1，），∴OA＝，连接AE，设点E到OA的距离为h，∴S△OAE＝＝AO•h，∴h＝，即点E到直线OA的距离是．
【点睛】此题考查了反比例函数系数k的几何意义，反比例函数图象上点的坐标特点，相似三角形的判定和性质，解一元二次方程，勾股定理等知识，熟练掌握反比例函数系数k的几何意义是解本题的关键．
11．如图，已知一次函数与反比例函数的图象交于点、，直线AB交x轴于点D，的面积等于3．
(1)求一次函数的解析式；
(2)直接写出不等式的解集；
(3)点P是直线AB图象上的动点，若CP把分成面积比等于2：3的两部分，求点P的坐标．
【答案】(1)
(2)或
(3)或
【分析】（1）利用反比例函数系数k的几何意义求得反比例函数的解析式，进而得出A，B的坐标，然后利用待定系数法求出一次函数的解析式即可；
（2）观察图象，写出一次函数的图象在反比例函数的图象上方时自变量的取值范围即可；
（3）过点作交延长线于，过作交于，设点的横坐标为，则其纵坐标为，求出，表示出，根据CP把分成面积比等于2：3的两部分分情况列式求出n的值即可解决问题．
（1）
解：点在反比例函数的图象上，轴于点，
，
反比例函数的解析式为，
把点、两点代入得：，，
、，
一次函数图象经过点、，
，
解得，
一次函数的解析式为；
（2）
观察图象可得：不等式的解集为：或；
（3）
轴，
，
当时，解得：，
，
，
如图：过点作交延长线于，过作交于，
设点的横坐标为，则其纵坐标为，
，，
当时，
，
解得：；
当时，
，
解得：，
当时，；当时，．
符合条件的点坐标为或．
【点睛】本题考查了反比例函数系数k的几何意义，待定系数法求一次函数的解析式，根据函数图象求不等式解集以及一次函数的实际应用等知识，注意数形结合思想的应用．
12．如图，直线与反比例函数在第一象限内的图象交于点，与y轴交于点B，过双曲线上的一点C作x轴的垂线，垂足为点D，交直线于点E，且．
(1)求k，p的值；
(2)若OE将四边形BOCE分成两个面积相等的三角形，求点C的坐标．
【答案】(1)，
(2)点的坐标为(4，2)
【分析】（1）先求出点B的坐标，得到，结合点A的横坐标为2，求出的面积，再利用求出，设，代入面积中求出k，得到反比例函数解析式，再将点A横坐标代入出点A纵坐标，最后将点A坐标代入直线即可求解；
（2）根据（1）中点C的坐标得到点E的坐标，结合OE将四边形BOCE分成两个面积相等的三角形，列出关于m的方程，解方程即可求解．
（1）
解：∵直线与y轴交点为B，
∴，
即．
∵点A的横坐标为2，
∴．
∵，
∴，
设，
∴，
解得．
∵点在双曲线上，
∴，
把点代入，得，
∴，；
（2）
解：由（1）得，
∴．
∵OE将四边形BOCE分成两个面积相等的三角形，
∴，
∵，，
∴，
解得或（不符合题意，舍去），
∴点的坐标为（4，2）．
【点睛】本题主要考查反比例函数的图形和性质，一次函数的图象和性质，熟练掌握一次函数和反比例函数的图象和性质及待定系数法求函数解析式是解题的关键．
13．如图，等腰的锐角顶点，的坐标分别为，，直角顶点在反比例函数的图象上．
(1)求的值；
(2)求的面积．
【答案】(1)9
(2)5
【分析】（1）过点 C分别向x轴、y轴作垂线，垂足分别为E，D，易证 ， 可得四边形OECD是正方形，则OD=OE，设，则，可解得x的值，进而得到点C的坐标；
（2）由勾股定理可得AC，BC的长度，根据等腰直角三角形面积的求法可得答案．
【详解】（1）如图，过点 C分别向x轴、y轴作垂线，垂足分别为E，D，
可得∠DCE=90°，
∵△ABC是等腰直角三角形，
∴BC=AC，∠BCA=∠BCD+∠DCA=90°，
∵∠DCA+∠ACE=90°，
∴∠BCD=∠ACE，
在△BDC和△AEC中，
∴（AAS），
∴，
设
由，可得，
∴.
解得
∴点的坐标为
∴
（2）由点A的坐标为（2，0），点C的坐标为（3，3），
可知AE=1，CE=3，在Rt△ACE中，由勾股定理可得，
由三角形ABC是等腰直角三角形可得，的面积为
【点睛】本题考查反比例函数的几何问题，正确作出辅助线，根据图形的性质，数形结合，是解题的关键．
14．如图，在平面直角坐标系中，点M为x正半轴上一点，过点M的直线轴，且直线分别与反比例函数和的图像交于两点，
(1)求k的值；
(2)当时，求直线OQ的解析式；
(3)在（2）的条件下，若x轴上有一点N，使得为等腰三角形，请直接写出所有满足条件的N点的坐标．
【答案】(1)-20
(2)y=﹣x
(3)点N的坐标为（，0）或（，0）或（﹣，0）或（，0）
【分析】(1）由 S△POQ= S△POM + S△MOQ =14结合反比例函数k的几何意义可得+4=14，进一步即可求出结果；
(2）由题意可得 MO=MQ ，于是可设点 Q ( a ,- a )，再利用待定系数法解答即可；
(3）先求出点Q的坐标和OQ的长，然后分三种情况：①若OQ=ON，可直接写出点N的坐标；②若QO=QN，根据等腰三角形的性质解答；③若 NO =NQ ，根据两点间的距离解答．
(1)
解：∵，S△POM=，S△QOM=，
∴+4=14，解得，
∵k＜0，
∴k=﹣20；
(2)
∵，轴，
∴，
∴MO=MQ，
设点Q（a，﹣a），直线OQ的解析式为y=mx，
把点Q的坐标代入得：﹣a=ma，解得：m=﹣1，
∴直线OQ的解析式为y=﹣x；
(3)
∵点Q（a，﹣a）在上，
∴，解得（负值舍去），
∴点Q的坐标为，则，
若为等腰三角形，可分三种情况：
①若OQ=ON=，则点N的坐标是（，0）或（﹣，0）；
②若QO=QN，则NO=2OM=，
∴点N的坐标是（，0）；
③若NO=NQ，设点N坐标为（n，0），则，解得，
∴点N的坐标是（，0）；
综上，满足条件的点N的坐标为（，0）或（，0）或（﹣，0）或（，0）．
【点睛】本题考查了反比例函数系数k的几何意义、等腰三角形的性质、勾股定理以及两点间的距离等知识，具有一定的综合性，熟练掌握相关知识是解题的关键．
15．如图，过C点的直线y＝﹣x﹣2与x轴，y轴分别交于点A，B两点，且BC＝AB，过点C作CH⊥x轴，垂足为点H，交反比例函数y＝（x＞0）的图象于点D，连接OD，△ODH的面积为6
（1）求k值和点D的坐标；
（2）如图，连接BD，OC，点E在直线y＝﹣x﹣2上，且位于第二象限内，若△BDE的面积是△OCD面积的2倍，求点E的坐标．
【答案】（1），点 D 坐标为（4，3）；（2）点E的坐标为（－8，2）
【分析】（1）结合反比例函数的几何意义即可求解值；由轴可知轴，利用平行线分线段成比例即可求解D点坐标；
（2）可知和的面积相等，由函数图像可知、、的面积关系，再结合题意，即可求CD边上高的关系，故作，垂足为F，即可求解E点横坐标，最后由E点在直线AB上即可求解．
【详解】解∶（1）设点 D 坐标为（m，n），
由题意得．
∵点 D在的图象上，．
∵直线的图象与轴交于点A，
∴点A 的坐标为（－4，0）．
∵CHx轴，CH//y 轴．．
点D在反比例函数的图象上，
点 D 坐标为（4，3）
（2）由（1）知轴，．
．
过点E作EFCD，垂足为点 F，交y轴于点M，
．
．
∴点 E 的横坐标为－8.
∵点E 在直线上，∴点E的坐标为（－8，2）．
【点睛】本题考查一次函数与反比例函数的综合运用、三角形面积问题、的几何意义，属于中档难度的综合题型．解题的关键是掌握一次函数与反比例函数的相关性质和数形结合思想．
16．如图，在平面直角坐标系中，点为正半轴上一点，过点的直线轴，且直线分别与反比例函数和的图像交于两点，.
求的值；
当时，求直线的解析式；
在的条件下，若轴上有一点，使得为等腰三角形，请直接写出所有满足条件的点的坐标.
【答案】（1）k=﹣20；（2）y=﹣x；（3）点N的坐标为（，0）或（，0）或（﹣，0）或（，0）．
【分析】（1）由结合反比例函数k的几何意义可得+4=14，进一步即可求出结果；
（2）由题意可得MO=MQ，于是可设点Q（a，﹣a），再利用待定系数法解答即可；
（3）先求出点Q的坐标和OQ的长，然后分三种情况：①若OQ=ON，可直接写出点N的坐标；②若QO=QN，根据等腰三角形的性质解答；③若NO=NQ，根据两点间的距离解答．
【详解】解：（1）∵，S△POM=，S△QOM=，
∴+4=14，解得，
∵k＜0，∴k=﹣20；
（2）∵，轴，
∴，
∴MO=MQ，
设点Q（a，﹣a），直线OQ的解析式为y=mx，
把点Q的坐标代入得：﹣a=ma，解得：m=﹣1，
∴直线OQ的解析式为y=﹣x；
（3）∵点Q（a，﹣a）在上，
∴，解得（负值舍去），
∴点Q的坐标为，则，
若为等腰三角形，可分三种情况：
①若OQ=ON=，则点N的坐标是（，0）或（﹣，0）；
②若QO=QN，则NO=2OM=，∴点N的坐标是（，0）；
③若NO=NQ，设点N坐标为（n，0），则，解得，∴点N的坐标是（，0）；
综上，满足条件的点N的坐标为（，0）或（，0）或（﹣，0）或（，0）．
【点睛】本题考查了反比例函数系数k的几何意义、等腰三角形的性质、勾股定理以及两点间的距离等知识，具有一定的综合性，熟练掌握相关知识是解题的关键．
17．如图，等边△ABC的顶点A，B分别在双曲线y＝的两个分支上，且AB经过原点O．BD⊥x轴于D，S△BOD＝2．
（1）直接写出该双曲线的解析式为_______；
（2）若OD＝2，求A、B、C点的坐标．
【答案】（1）y＝﹣；（2）C（2，2）．
【分析】（1）根据反比例函数系数k的几何意义即可求得k的值，从而求得解析式；
（2）把B的横坐标代入解析式即可求得B的坐标，根据反比例函数图象的对称性可得OA＝OB，即可求得A坐标，根据等边三角形三线合一可证明△COE∽△OBD，根据相似三角形的性质可得C的坐标．
【详解】解：（1）∵点B在双曲线y＝的图象上，且BD⊥x轴于D，
∴S△BOD＝|k|，
∵S△BOD＝2，
∴|k|＝4，
∵图象在二四象限，
∴k＝﹣4，
∴反比例函数的解析式为y＝﹣，
故答案为y＝﹣；
（2）作CE⊥x轴于E，连接OC，
∵OD＝2，
∴B的横坐标为2，
把x＝2代入y＝﹣，求得y＝﹣2，
∴B（2，﹣2），
∵A、B关于原点对称，
∴A（﹣2，2），
∵反比例函数的图象关于原点对称，
∴OA＝OB，
∵△ABC是等边三角形，
∴OC⊥AB，
∴∠BOC＝90°，∠BCO＝30°，
∴tan∠BCO＝＝，
∴∠COE+∠BOD＝90°，
∵CE⊥x轴，BD⊥x轴，
∴∠CEO＝∠ODB＝∠COE+∠OCE＝90°，
∴∠BOD＝∠OCE，
∴△COE∽△OBD，
∴，即，
∴OE＝CE＝2，
∴C（2，2）．
【点睛】本题主要考查了反比例函数的综合，准确计算是解题的关键．
18．如图，矩形OABC的两个顶点A，C分别在y轴和x轴上，边AB和BC与反比例函数y1＝（x0）和y2＝（k0，x0）图象交于E，F和点H，G．AE：AF＝2：3．
（1）求反比例函数y2的解析式；
（2）若点C的坐标为（8，0），求GH的长．
【答案】（1） ；（2）
【分析】（1）设E（a，b），根据已知条件求得F（a，b），分别代入解析式得出ab＝4，a•b＝k，从而求得k＝6，D得出反比例函数y2的解析式；
（2）把x＝8分别代入y1＝和y2＝，即可求得CG、CH的值，然后根据GH＝CG﹣CH即可求得．
【详解】解：（1）设E（a，b），
∴AE＝a，
∵AE：AF＝2：3．
∴AF＝a，
∴F（a，b），
∵E是反比例函数y1＝（x＞0）上的点，
∴ab＝4，
∵F是反比例函数（k＞0，x＞0）图象上的点，
∴a•b＝k，
∴k＝×4＝6，
∴反比例函数y2的解析式为y2＝．
（2）把x＝8分别代入y1＝和y2＝得，y1＝和y2＝，
∴CH＝，CG＝，
∴GH＝CG﹣CH＝．
【点睛】本题考查了待定系数法求反比例函数的解析式以及反比例函数图象上点的坐标特征，利用形数结合解决此类问题，是非常有效的方法．
19．如图，点、分别在反比例函数和的图象上，线段与轴相交于点．
(1)如图①，若轴，且，．求、的值；
(2)如图②，若点是线段的中点，且的面积为2．求的值．
【答案】(1)，；
(2)．
【分析】（1）连接、，根据反比例函数系数的几何意义以及得到，即①，由②．①②得，，进而求得；
（2）作轴于，轴于，则，，根据题意得到，，即可得到，整理得．
（1）解：如图①，连接、，轴，，，，，即，①，②．①②得，，；
（2）如图②，作轴于，轴于，则，，点是线段的中点，且的面积为2，，在和中，，，，，整理得．
【点睛】本题考查了反比例函数系数的几何意义，反比例函数的性质，正确作出辅助线是解题的关键．
20．（1）探究新知：
如图，已知三角形ABC与三角形ABD的面积相等，试判断AB与CD的位置关系，并说明理由．
（2）结论应用：
如图，点M、N在反比例函数的图像是哪个，过点M作ME⊥y轴，过点N作NF⊥x轴，垂足分别为E、F，试证明：．
【答案】（1），见解析（2）见解析
【分析】(1) 分别作两个三角形公共边上的高，由面积相等，则高相等，又同一直线上的两高平行，得四边形CDFE为矩形，则AB与CD的位置关系得定；
(2) 连接MF、NE，先证明S △MEF=S △NEF，然后再运用(1) 中的结论得证
【详解】（1）分别过点C，D，作CG⊥AB，DH⊥AB，垂足为G，H，
则∠CGA=∠DHB=90°，CG∥DH．
∵△ABC与△ABD的面积相等，
∴ CG=DH；
∴ 四边形CGHD为平行四边形．
∴ AB∥CD．
(2)证明：连接MF，NE 设点M的坐标为(x1，y1)，点N的坐标为(x2，y2)．
∵点M，N在反比例函数 (k>0)的图像上，
∴ ．
∵ME⊥y轴，NF⊥x轴，
∴ OE=y1，OF=x2．
∴ S △EFM=
S △EFN= ．
∴S △EFM =S △EFN．
所以由(1)中的结论可知：MN∥EF．
【点睛】此题由浅入深探究问题，体现了数学化归思想．是一类比较创新的题型．同学们要擅于归纳总结
21．六•一儿童节，小文到公园游玩．看到公园的一段人行弯道MN（不计宽度），如图，它与两面互相垂直的围墙OP、OQ之间有一块空地MPOQN（MP⊥OP，NQ⊥OQ），他发现弯道MN上任一点到两边围墙的垂线段与围墙所围成的矩形的面积都相等，比如：A、B、C是弯道MN上的三点，矩形ADOG、矩形BEOH、矩形CFOI的面积相等．爱好数学的他建立了平面直角坐标系（如图），图中三块阴影部分的面积分别记为S1、S2、S3，并测得S2=6（单位：平方米）．OG=GH=HI．
（1）求S1和S3的值；
（2）设T（x，y）是弯道MN上的任一点，写出y关于x的函数关系式；
（3）公园准备对区域MPOQN内部进行绿化改造，在横坐标、纵坐标都是偶数的点处种植花木（区域边界上的点除外），已知MP=2米，NQ=3米．问一共能种植多少棵花木？
【答案】（1）；（2）；（3）17.
【分析】（1）矩形ADOG、矩形BEOH、矩形CFOI的面积相等列方程组求解即可.
（2）由道MN上任一点到两边围墙的垂线段与围墙所围成的矩形的面积相等列式可得.
（3）把区域MPOQN内满足条件的点一一列出即可求解.
【详解】解：（1）∵矩形ADOG、矩形BEOH、矩形CFOI的面积相等，且OG=GH=HI，
∴.
又∵S2=6，
∴，
解得.
（2）∵点T是弯道MN上的任一点，
∴根据弯道MN上任一点到两边围墙的垂线段与围墙所围成的矩形的面积相等得.
∴y关于x的函数关系式为.
（3）∵MP=2，NQ=3，
∴当x=2时，y=18；
∵横坐标、纵坐标都是偶数，
∴当x=4，6，8，10时，
y=9，6，.
∴区域MPOQN内满足条件的点为（2，2），（2，4），（2，6），（2，8），（2，10），（2，12），（2，14），（2，16），（4，2），（4，4），（4，6），（4，8），（6，2），（6，4），（8，2），（8，4），（10，2），计17个.
考点：1.反比例函数综合题；2.由实际问题列函数关系式；3.曲线上点的坐标与方程的关系；4.点的坐标；5.分类思想和方程思想的应用.