人教版八年级数学下册 第十八章 平行四边形第一课时 平行四边形的边、角性质（课件）

这是一份人教版八年级数学下册 第十八章 平行四边形第一课时 平行四边形的边、角性质（课件），共23页。
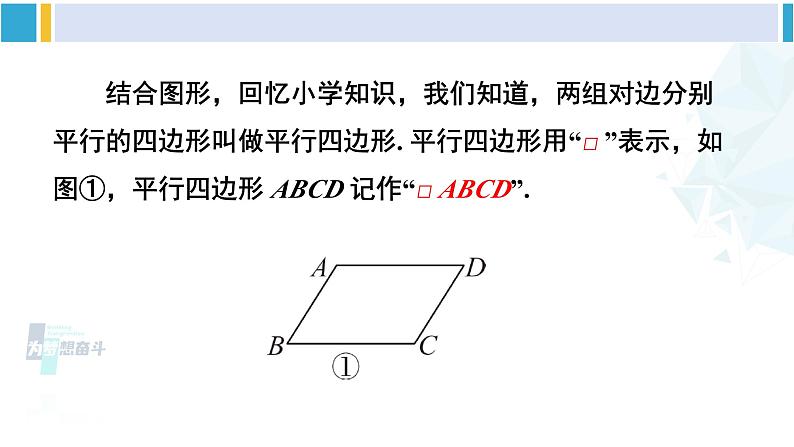
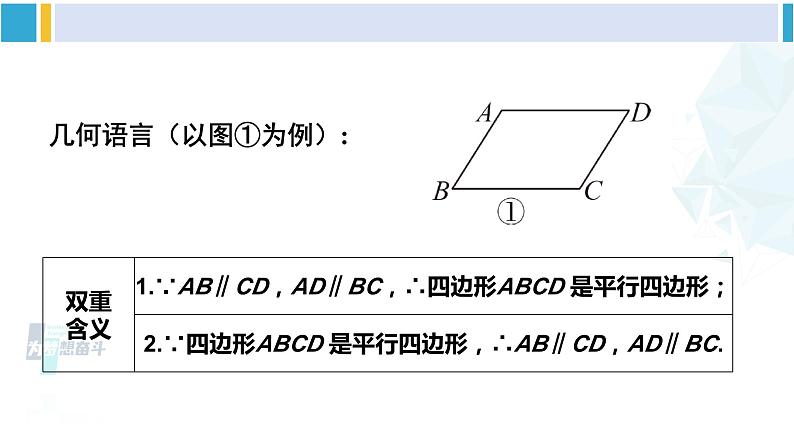
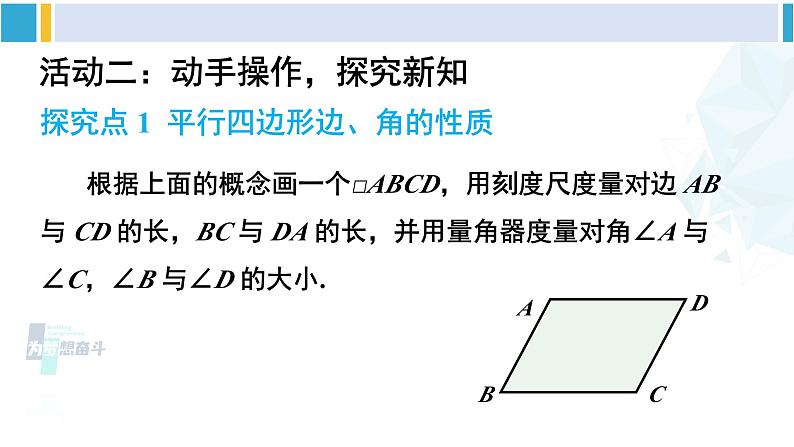
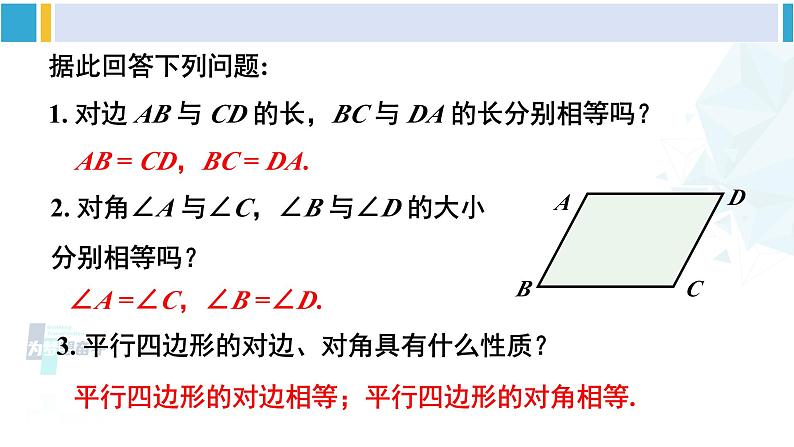
人教版八年级下册平行四边形的边、角性质活动一：创设情境，导入新课【情境导入】 仔细观察下列实际生活中的图片，你能从中找到平行四边形的形象吗？ 结合图形，回忆小学知识，我们知道，两组对边分别平行的四边形叫做平行四边形. 平行四边形用“□ ”表示，如图①，平行四边形 ABCD 记作“□ ABCD”.几何语言（以图①为例）:动手试一试:：如图②，在□ ABCD 中，EF∥BC，则图中共有______个平行四边形.3活动二：动手操作，探究新知探究点 1 平行四边形边、角的性质 根据上面的概念画一个□ABCD，用刻度尺度量对边 AB 与 CD 的长，BC 与 DA 的长，并用量角器度量对角∠A 与∠C，∠B 与∠D 的大小.据此回答下列问题:1. 对边 AB 与 CD 的长，BC 与 DA 的长分别相等吗？AB = CD，BC = DA.2. 对角∠A 与∠C，∠B 与∠D 的大小分别相等吗？∠A =∠C，∠B =∠D.3. 平行四边形的对边、对角具有什么性质？平行四边形的对边相等；平行四边形的对角相等.下面我们一起来进行验证.已知:如图，四边形 ABCD 是平行四边形.求证: AB = CD，BC = DA ；∠B =∠D，∠BAD =∠DCB.证明:如图，连接 AC.∵四边形 ABCD 是平行四边形，∴AD // BC，AB // CD. ∴∠1=∠2，∠3=∠4.又 AC 是△ABC 和△CDA 的公共边，∴△ABC≌△CDA. ∴AB = CD，BC = DA，∠B =∠D.∵∠1=∠2，∠3=∠4，∴∠1＋∠4 = ∠2＋∠3，即∠BAD = ∠DCB.归纳总结:平行四边形的对边相等；平行四边形的对角相等.　　例1 如图，□ ABCD中，DE⊥AB，BF⊥CD，垂足分别为 E，F．求证：AE = CF．证明： ∵四边形 ABCD 是平行四边形，∴ ∠A = ∠C，AD = CB.又∠AED = ∠CFB = 90°，∴ △ADE ≌△CBF，∴ AE = CF. [选自教材P42][选自教材P43]练习 1.在 □ ABCD 中，（1）已知 AB = 5，BC = 3，求它的周长；（2）已知 ∠A = 38°，求其余各内角的度数.解：（1）∵四边形 ABCD 是平行四边形，∴AB = CD = 5，BC = AD = 3，∴它的周长 = (5+3)×2 = 16.（2）∵四边形 ABCD 是平行四边形，∴∠C = ∠A，∠A + ∠B = 180°，∠A+∠D = 180°.∵∠A = 38°，∴∠C = 38°，∴∠D = ∠B = 180°-38°= 142°.[选自教材P43]练习 1.在 □ ABCD 中，（1）已知 AB = 5，BC = 3，求它的周长；（2）已知 ∠A = 38°，求其余各内角的度数.2. 如图，在□ ABCD 中，E，F 分别是 AB，CD 的中点. 求证:∠ADE = ∠CBF.证明:∵四边形 ABCD 是平行四边形，∴∠A =∠C，AD = CB，AB = CD.∵E，F 分别是 AB，CD 的中点，∴AE = AB，CF = CD. ∴AE = CF.∴△AED≌△CFB (SAS).∴△ADE=∠CBF.探究点 2 两条平行线之间的距离 利用方格纸画出直线 a//b，A，D 为直线 a 上任意两点. 1.如图①，过点 A，D 分别画直线 c，d，使 c∥d，B，C 分别是直线 c 和 b，直线 d 和 b 的交点，用刻度尺测量点 A，B 的距离和点 D，C 的距离，它们相等吗？_____相等 2. 再测量一下点 A，D 的距离和点 B，C 的距离，它们相等吗？______相等归纳总结: 两条平行线之间的任何两条平行线段都相等.（可结合平行四边形的概念和性质说明其中的道理） 3.如图②，分别过 A，D 两点作直线 b 的垂线 AB 和 DC. AB 和 DC 有什么关系？___________________ AB // DC，AB = DC 概念引入: 从上面的结论进一步可以知道: 如果两条直线平行，那么一条直线上所有的点到另一条直线的距离都相等. 两条平行线中，一条直线上任意一点到另一条直线的距离，叫做这两条平行线之间的距离. 图②中 AB，CD 均可表示平行线 a，b 之间的距离.【对应训练】1.如图，已知 l1 // l2，AB // CD，CE⊥l2，FG⊥l2，下列说法错误的是（ ）A. l1 与 l2 之间的距离是线段 FG 的长度B. 线段 CD 的长度就是 l1，l2 之间的距离C. AC = BDD. CE = FGB 2.如图，剪两张对边平行的纸条，随意交叉叠放在一起，重合的部分构成了个四边形，转动其中一张纸条，线段 AD 和 BC 的长度有什么关系？为什么？解：线段 AD = BC. ∵两张纸条的对边都平行，∴重合的部分构成的四边形是平行四边形，平行四边形的对边相等，∴ AD = BC.活动三：综合运用，巩固提升 例2 如图，在△ABC 中，AB = AC，点 D 在 AC 边上，以 CB，CD 为边作 □ BCDE，DE 交 AB 于点 F. （1）若∠A = 50°，求 ∠E 的度数；解: 在△ABC中，∵∠A = 50°，AB = AC， ∴∠C =∠ABC = (180°-50°)÷2 = 65°.∵四边形 BCDE 是平行四边形，∴∠E = ∠C = 65°. 例2 如图，在△ABC 中，AB = AC，点 D 在 AC 边上，以 CB，CD 为边作 □ BCDE，DE 交 AB 于点 F. （2）若 AD = CD，BC = 6，求 EF 的长.活动三：综合运用，巩固提升∵四边形 BCDE 是平行四边形，∴BE // CD，DE = BC = 6，BE = CD，∴∠E =∠ADF，∠EBF =∠A.∵AD = CD，BE = AD.∴△BEF≌△ADF (ASA). ∴EF = DF = DE = 3. 平行四边形的概念是什么？平行四边形的边、角有哪些性质？两条平行线之间的距离是指什么？1.教材 P49 习题 18.1 第 1，2，7，8 题.2.《创优作业》主体本部分相应课时训练.