人教版八年级数学下册 第十八章 平行四边形第二课时 平行四边形对角线的性质（课件）

这是一份人教版八年级数学下册 第十八章 平行四边形第二课时 平行四边形对角线的性质（课件），共23页。

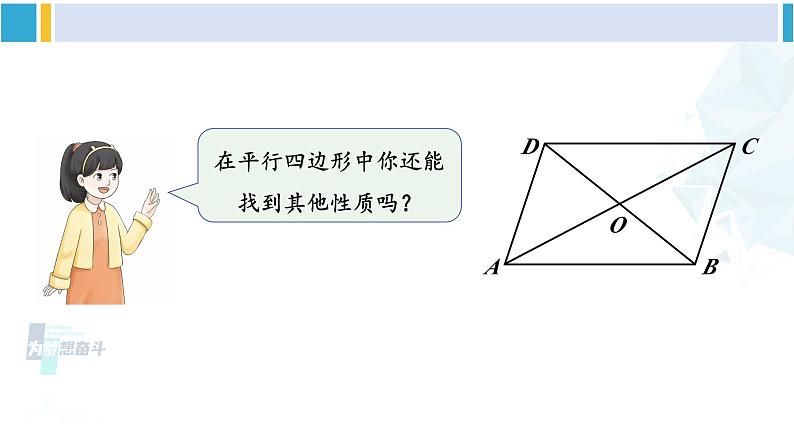
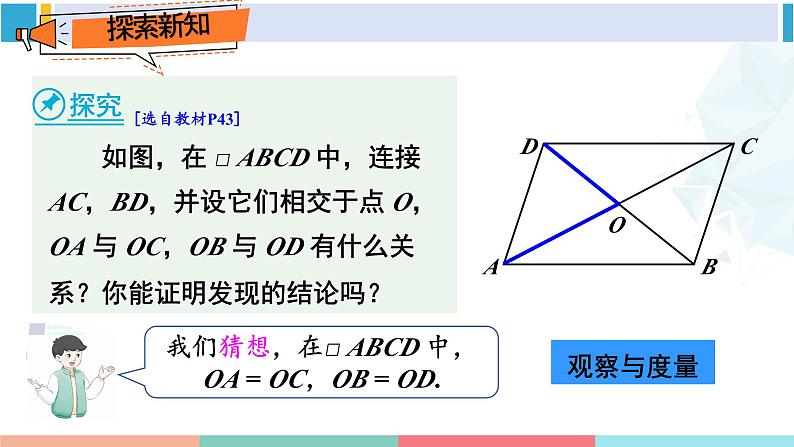
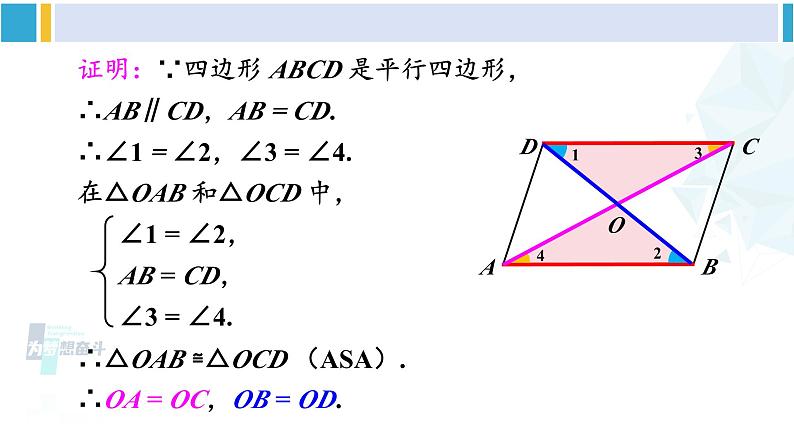
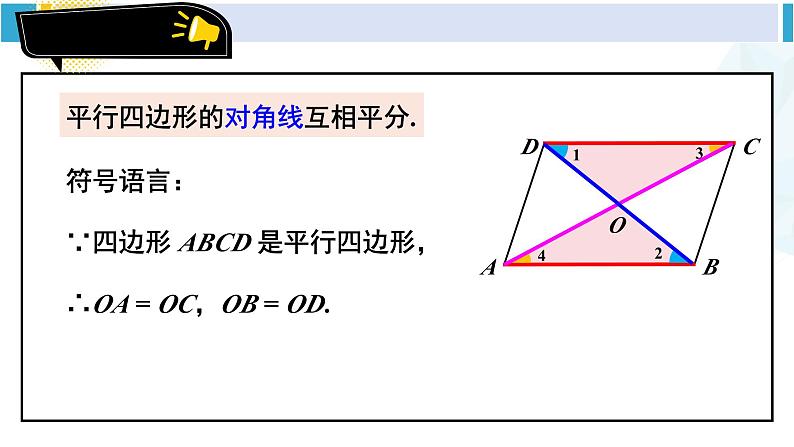
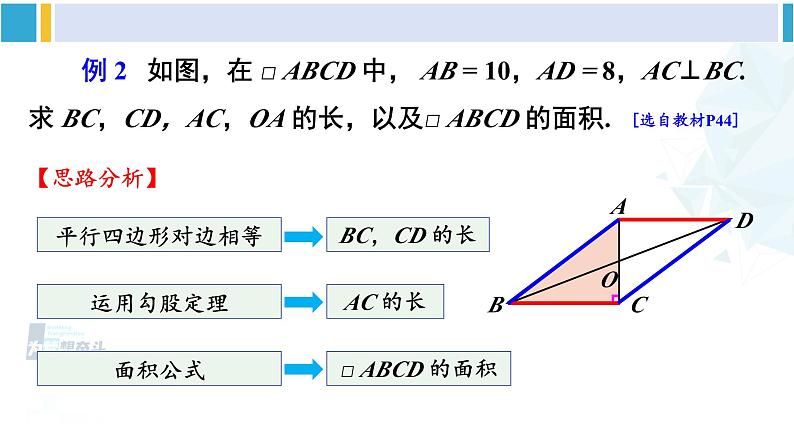
人教版八年级下册平行四边形对角线的性质前面我们学习了平行四边形的哪些知识点？定义：两组对边分别平行的四边形叫作平行四边形。性质1：平行四边形的对边相等。性质2：平行四边形的对角相等。在平行四边形中你还能找到其他性质吗？ 如图，在 □ ABCD 中，连接 AC，BD，并设它们相交于点 O，OA 与 OC，OB 与 OD 有什么关系？你能证明发现的结论吗？观察与度量[选自教材P43]证明：∵四边形 ABCD 是平行四边形，∴AB∥CD，AB = CD.∴∠1 = ∠2，∠3 = ∠4.在△OAB 和△OCD 中，∴△OAB ≌△OCD （ASA）.∴OA = OC，OB = OD.平行四边形的对角线互相平分.符号语言：∵四边形 ABCD 是平行四边形，∴OA = OC，OB = OD.小 结 例 2 如图，在 □ ABCD 中， AB = 10，AD = 8，AC⊥BC.求 BC，CD，AC，OA 的长，以及□ ABCD 的面积.[选自教材P44]【思路分析】平行四边形对边相等BC，CD 的长运用勾股定理AC 的长面积公式□ ABCD 的面积解：∵四边形 ABCD 是平行四边形，∴ BC = AD = 8， CD = AB = 10.∵ AC ⊥ BC，∴ △ABC 是直角三角形.根据勾股定理，又 OA = OC， 例 2 如图，在 □ ABCD 中， AB = 10，AD = 8，AC⊥BC.求 BC，CD，AC，OA 的长，以及□ ABCD 的面积.[选自教材P44] 一位饱经沧桑的老人经过一辈子的辛勤劳动拥有了一块平行四边形形状的土地．由于年老体弱，他决定把这块土地平分给他的四个孩子，他是按下图这样分的：       可是当四个孩子看到时，争论不休，都认为自己分的土地比其他人少．老人这样分地合理吗？面积探索说一说，△ABO，△BCO，△CDO，△DAO 它们的面积有什么关系？平行四边形的对角线互相平分.【提示】三角形中线等分面积.面积探索说一说，△ABO，△BCO，△CDO，△DAO 它们的面积有什么关系？在△ABD中，OB = OD，OA 是 BD 边上的中线，所以 S△ABO = S△DAO .同理可得：S△ABO = S△BCO = S△CDO = S△DAO .面积探索说一说，△ABO，△BCO，△CDO，△DAO 它们的面积有什么关系？归纳：平行四边形的两条对角线将它分成的四个三角形的面积都相等.面积探索想一想 △ABD 的面积与 △CDB 的面积有什么关系？△ABC 的面积与△CDA 的面积呢？因为 S△ABD = S△ABO + S△DAO ，S△CDB = S△BCO + S△CDO ，所以 S△ABD = S△CDB .同理可得，S△ABC = S△CDA .发现：任意相邻两个小三角形组成的大三角形的面积也相等.面积探索 如图，在 □ ABCD 中，BC = 10，AC = 8，BD = 14，△AOD 的周长是多少？△ABC 与△DBC 的周长哪个长？长多少？[选自教材P44 练习]解：∵四边形 ABCD 是平行四边形，∴AD＝ BC＝10，OA＝ OC ＝ 4，OD＝ OB ＝ 7，∴ l△AOD＝ AD+OA+OD＝10+4+7＝21，∵ AB=CD，BC=BC，BD – AC=14 – 8 = 6，∴△DBC 的周长较长，长 6.△ABO 与△ADO 的周长呢？周长探索 如图， □ ABCD 的对角线 AC ，BD 相交于点 O，EF 过 点 O 且与 AB，CD 分别相交于点 E，F . 求证 OE = OF.【思路分析】△AOE ≌△COFOE = OF[选自教材P44 练习]综合探索证明：∵四边形ABCD是平行四边形，∴AB∥CD，OA=OC （平行四边形的性质）∴∠EAO=∠FCO（两直线平行，内错角相等）在△AOE和△COF中， ∠AOE = ∠ COF﹙对顶角相等﹚ OA = OC ∠EAO = ∠FCO∴ △AOE≌△COF （ASA ）∴ OE = OF （全等三角形的对应边相等） 如图， □ ABCD 的对角线 AC ，BD 相交于点 O，EF 过 点 O 且与 AB，CD 分别相交于点 E，F . 求证 OE = OF.[选自教材P44 练习]综合探索改变直线 EF 的位置，OE = OF 还成立吗？ □ ABCD 被线段 EF 所截的两部分面积与周长呢？点击打开几何画板演示1. 如图， □ ABCD 中，AD = 5，BD = 6， AC = a，则 a 的取值范围是（ ） A．2