人教版八年级数学下册 第十九章 一次函数第二课时 一次函数的图象与性质（课件）

这是一份人教版八年级数学下册 第十九章 一次函数第二课时 一次函数的图象与性质（课件），共22页。
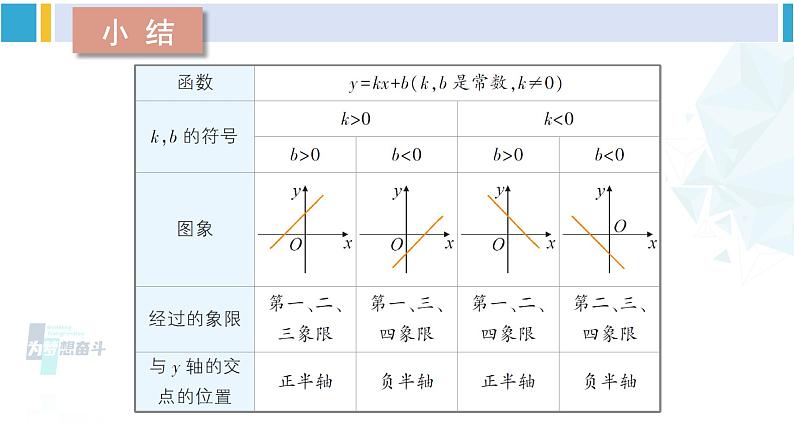
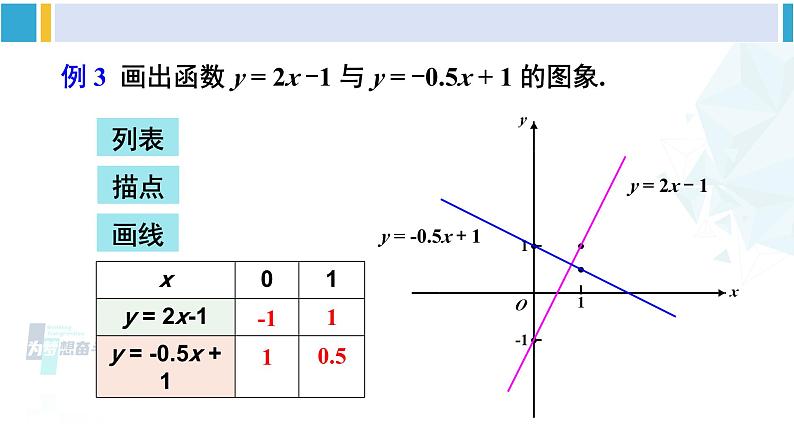
一次函数的图象与性质 正比例函数图象例 2 画出函数 y = -6x 与 y = -6x + 5 的图象.列表描点画线1260-6-1217115-1-7y = -6x y = -6x + 5 比较这两个函数图象的相同点与不同点，填出你的观察结果： 这两个函数的图象形状都是________，并且倾斜程度______. 函数 y = -6x 的图象经过原点，函数 y = -6x + 5 的图象与 y 轴交于点______，即它可以看作由直线y = -6x 向____平移_____个单位长度得到.一条直线相同(0，5)上5思 考y = -6x y = -6x + 5 联系上面的结果，你能归纳出一次函数 y = kx + b(k ≠ 0) 与正比例函数y = kx (k≠0) 之间的关系吗？y = -6x y = -6x + 5 直线 y = kx + b (k≠0) 可以看作由直线 y = kx (k≠0) 平移 | b | 个单位长度得到.当 b > 0 时，向上平移；当 b < 0 时，向下平移 .小 结一次函数图象的画法：根据两点确定一条直线，为计算简单，一般选择点（0，b）和点（1，k+b）.例 3 画出函数 y = 2x -1 与 y = -0.5x + 1 的图象.列表描点画线-11y = 2x - 1 10.5y = -0.5x + 1 例 3 画出函数 y = 2x -1 与 y = -0.5x + 1 的图象.你还有其他画法吗？ 先画直线 y = 2x 与 y = -0.5x，再分别平移它们，也能得到直线 y = 2x-1 与 y = -0.5x + 1.- 1 + 1 探 究 画出函数 y = x + 1，y = -x + 1，y = 2x + 1，y = -2x + 1 的图象. 由它们联想：一次函数解析式 y = kx + b（k，b 是常数，k ≠ 0）中，k 的正负对函数图象有什么影响？1210131-1当 k > 0 时，y 随 x 的增大而增大；当 k < 0 时，y 随 x 的增大而减小.[选自教材P93]练习1. 直线 y = 2x - 3 与 x 轴交点坐标为______，与 y 轴 交点坐标为_______，图象经过____________象限， y 随 x 的增大而______.(0，-3)一、三、四增大2. 在同一直角坐标系中画出下列函数的图象，并指出 每小题中三个函数的图象有什么关系. （1）y = x -1， y = x， y = x + 1；y = x -1y = xy = x + 12. 在同一直角坐标系中画出下列函数的图象，并指出 每小题中三个函数的图象有什么关系. （2）y = -2x -1， y = -2x， y = -2x+1.每小题中三个函数的图象都互相平行.3. 分别在同一直角坐标系中画出下列（1）（2）中各函数 的图象，并指出每组函数图象的共同之处.（1）y = x + 1， y = x + 1， y = 2x + 1；3. 分别在同一直角坐标系中画出下列（1）（2）中各函数 的图象，并指出每组函数图象的共同之处.（2）y = - x - 1， y = -x - 1， y = -2x - 1.每小题中三个函数的图象与 y 轴交点为同一点，只是倾斜程度不同.题型一 一次函数的图象与性质已知关于 x 的一次函数 y = （2m+4）x+（3-n）.（1）当 m，n 取何值时，y 随 x 的增大而减小？（2）当 m，n 取何值时，图象经过第一、二、三象限？ 题型一 一次函数的图象与性质已知关于 x 的一次函数 y = （2m+4）x+（3-n）.（1）当 m，n 取何值时，y 随 x 的增大而减小？（2）当 m，n 取何值时，图象经过第一、二、三象限？ 解：（1）由题意，得 2m + 4 < 0，3-n 是任意实数，所以 m < -2，n 是任意实数.（2）由题意，得 2m + 4 > 0，3-n > 0，所以 m > -2，n < 3.题型二 平面直角坐标系中的双图象共存问题关于 x 的一次函数 y = mx + n 与 y = mnx（mn ≠ 0）在同一平面直角坐标系中的大致图象可能是（ ） C题型三 一次函数的图象和性质与几何的综合如图，函数 y = kx + 1 的图象经过点 A（3，-3），且与 x 轴相交于点 B，O 为坐标原点，连接 OA.（1）求点 B 的坐标；（2）求△OAB 的面积.题型三 一次函数的图象和性质与几何的综合如图，函数 y = kx + 1 的图象经过点 A（3，-3），且与 x 轴相交于点 B，O 为坐标原点，连接 OA.（1）求点 B 的坐标；（2）求△OAB 的面积.一次函数解析式y = kx + b（k，b是常数，k ≠ 0）图象的位置当 k > 0，b > 0 时，图象经过一、二、三象限当 k > 0，b < 0 时，图象经过一、三、四象限当 k < 0，b > 0 时，图象经过一、二、四象限当 k < 0，b < 0 时，图象经过二、三、四象限性质当 k > 0 时，y 随 x 的增大而增大.当 k < 0 时，y 随 x 的增大而减小.