人教版八年级数学下册 第十九章 一次函数第二课时 正比例函数的图象与性质（课件）

这是一份人教版八年级数学下册 第十九章 一次函数第二课时 正比例函数的图象与性质（课件），共21页。

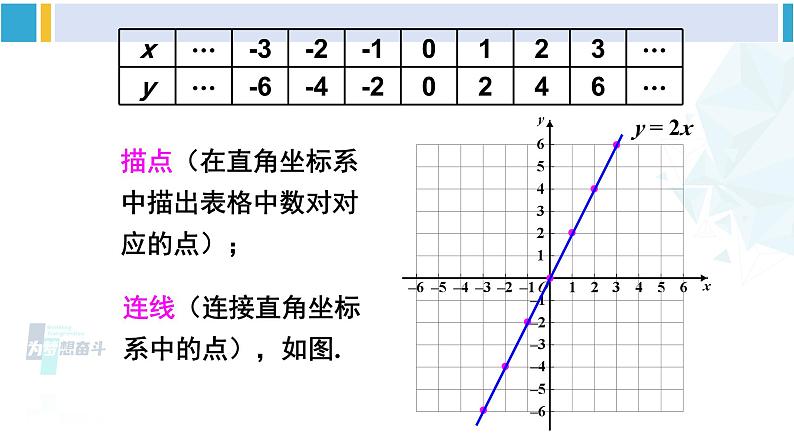
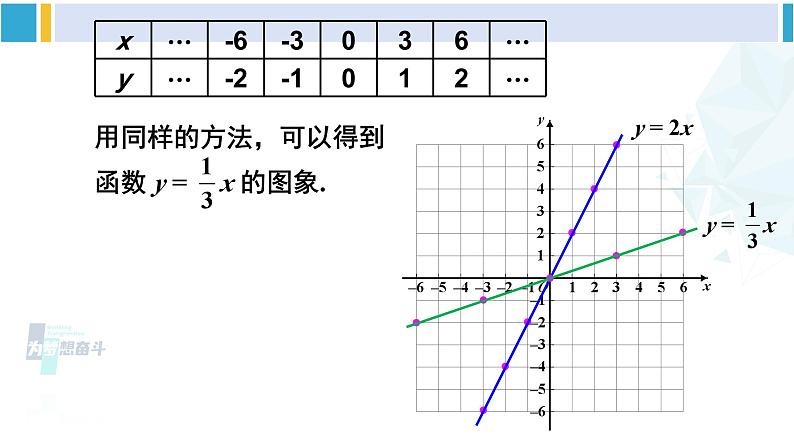
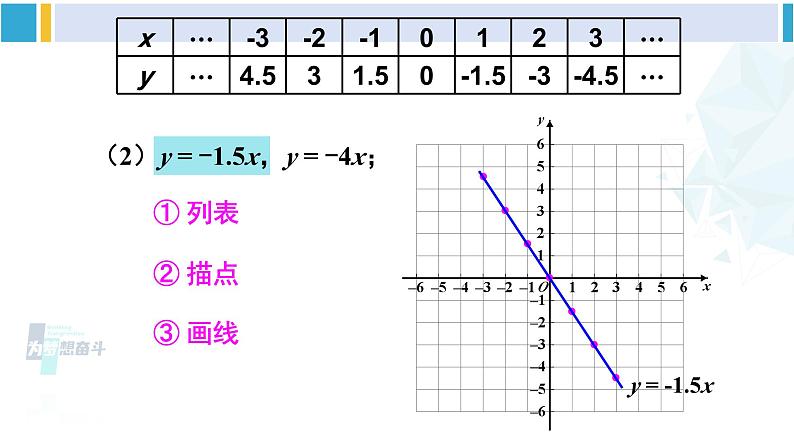
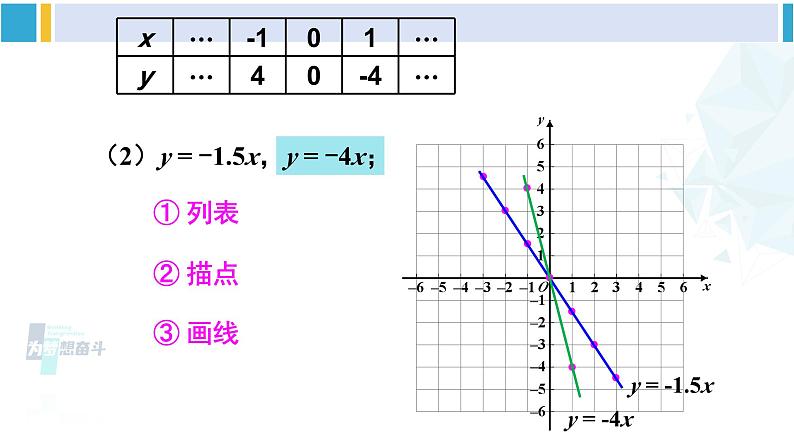
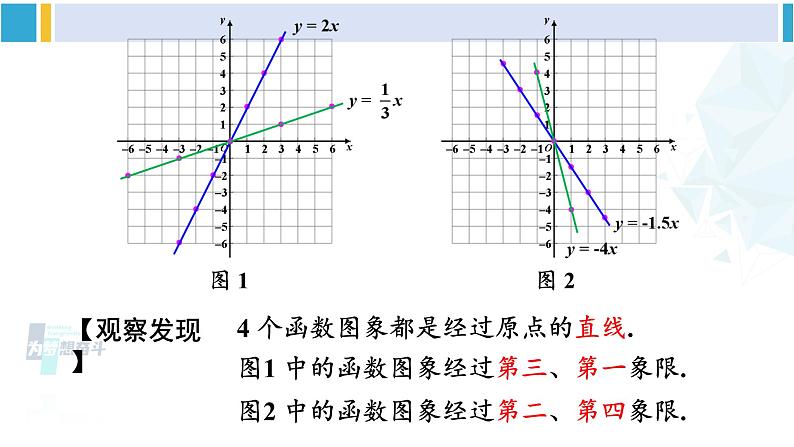
正比例函数的图象与性质例 1 画出下列正比例函数的图象：解：函数 y = 2x 中自变量 x 可为任意实数. 列表如下： 探索新知描点（在直角坐标系中描出表格中数对对应的点）；连线（连接直角坐标系中的点），如图.y = 2xy = 2x（2）y = -1.5x，y = -4x； ① 列表 ② 描点 ③ 画线 y = -1.5x（2）y = -1.5x，y = -4x；y = -1.5x ① 列表 ② 描点 ③ 画线 y = -4x图 1图 2【观察发现】4 个函数图象都是经过原点的直线.图1 中的函数图象经过第三、第一象限.图2 中的函数图象经过第二、第四象限. 一般地，正比例函数 y = kx（k 是常数，k ≠ 0）的图象是一条经过原点的直线，我们称它为直线 y = kx.小 结当 k > 0 时，直线 y = kx 从左向右上升，即随着 x 的增大 y 也增大；当 k < 0 时，直线 y = kx 从左向右下降，即随着 x 的增大 y 反而减小； 经过原点与点（1，k）（k 是常数，k ≠ 0）的直线是哪个函数的图象？画正比例函数的图象时，怎样画最简单？为什么？因为两点确定一条直线，所以可用两点法画正比例函数 y = kx (k ≠ 0) 的图象.一般地，过原点和点(1，k)(k 是常数，k ≠ 0) 的直线，即正比例函数 y = kx (k ≠ 0) 的图象.思 考[选自教材P89]练习用你认为最简单的方法画出下列函数的图象：（2）y = -3x.y = -3x已知 y 是 x 的正比例函数，且函数图象经过点 A(-3，6).（1）求 y 关于 x 函数解析式；（2）当 x = -6 时，求对应的函数值 y；（3）当 y = 2 时，求 x 的值.解：（1）设正比例函数的解析式为 y = kx（k ≠ 0）.因为图象经过点 A(-3，6)，所以 -3k = 6，解得 k = -2. 所以 y 关于 x 的函数解析式是 y = -2x.（2）把 x = -6 代入 y = -2x，可得 y = 12.（3）把 y = 2 代入 y = -2x，可得 x = -1.求正比例函数解析式的步骤：（1）设：设出正比例函数解析式 y = kx（k 是常数，k ≠ 0）；（2）代：将一组 x，y 的值代入函数解析式，得到关于 k 的方程；（3）求：解方程求出 k 的值；（4）写：写出正比例函数解析式.1.已知关于 x 的正比例函数 y = (m+1) ，若 y 随 x 的增大而减小，则 m 的值为______.-2巩固练习2.如图，三个正比例函数的图象分别对应解析式：① y = ax；② y = bx；③ y = cx. 将 a，b，c 从小到大排列为（ ）A. a < b < c B. a < c < b C. b < a < c D. c < b < aB3.已知 y = y1+y2，y1与 x 成正比例，y2 与 x-1 成正比例，且当 x = 3 时，y = 4；当 x = 1是，y = 2. 求 y 关于 x 的函数解析式.某商品的售价 y（单位：元）与质量 x（单位：kg）之间的关系如下表：（1）由上表写出售价 y 随质量 x 变化的函数解析式，并画出函数的图象；（2）购买 5.5 kg 这种商品应付多少元？ 解：（1）由表中数据观察到质量 x 每增加 1 kg，售价就增加 2.4 元，这样的变化规律可以表示为 y = 2.4x（x ≥ 0）. 这个函数的图象如图所示.（2）当 x = 5.5 时，y = 2.4×5.5 = 13.2，所以购买 5.5 kg 这种商品应付 13.2 元.正比例函数的图象和性质图象：性质：经过原点的直线当 k > 0 时，经过第三、第一象限当 k < 0 时，经过第二、第四象限当 k > 0 时，直线 y = kx 从左向右上升，即随着 x 的增大 y 也增大；当 k < 0 时，直线 y = kx 从左向右下降，即随着 x 的增大 y 反而减小；课堂小结1.从课后习题中选取；2.完成练习册本课时的习题.课后作业