四川省宜宾市叙州区第二中学2024届高三上学期期末数学（文）试卷（Word版附解析）

这是一份四川省宜宾市叙州区第二中学2024届高三上学期期末数学（文）试卷（Word版附解析），文件包含四川省宜宾市叙州区第二中学校2024届高三上学期期末数学文试题Word版含解析docx、四川省宜宾市叙州区第二中学校2024届高三上学期期末数学文试题Word版无答案docx等2份试卷配套教学资源，其中试卷共28页， 欢迎下载使用。
第Ⅰ卷 选择题
一、选择题：本题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的．
1. 已知集合，，则（ ）
A. B. C. D.
【答案】B
【解析】
【分析】根据对数函数的性质求出集合，再根据一元二次方程求出集合，最后根据并集的定义计算可得.
【详解】解：由，即，解得，所以，
由，即，解得，所以，
所以.
故选：B
2. 已知复数，i为虚数单位，则z的共轭复数为（ ）
A. B. C. D.
【答案】B
【解析】
【分析】根据复数的运算公式求复数的代数形式，再求其共轭复数即可.
【详解】，
所以z的共轭复数为，
故选：B.
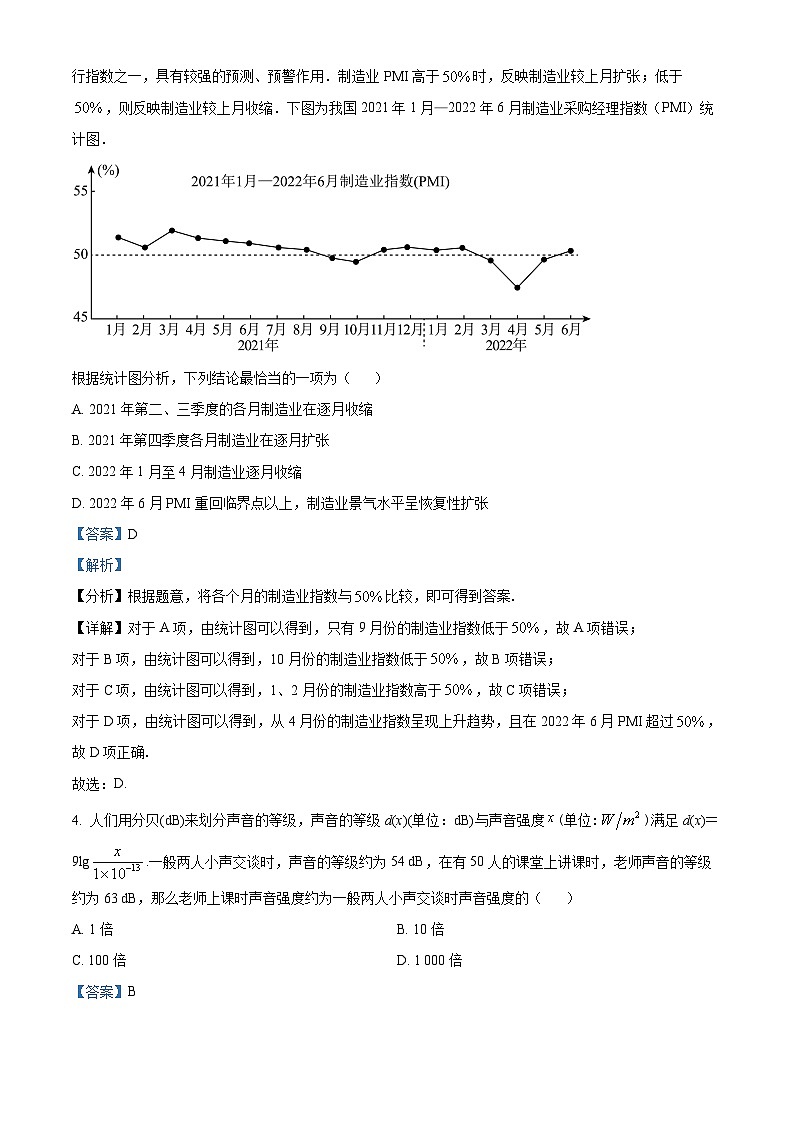
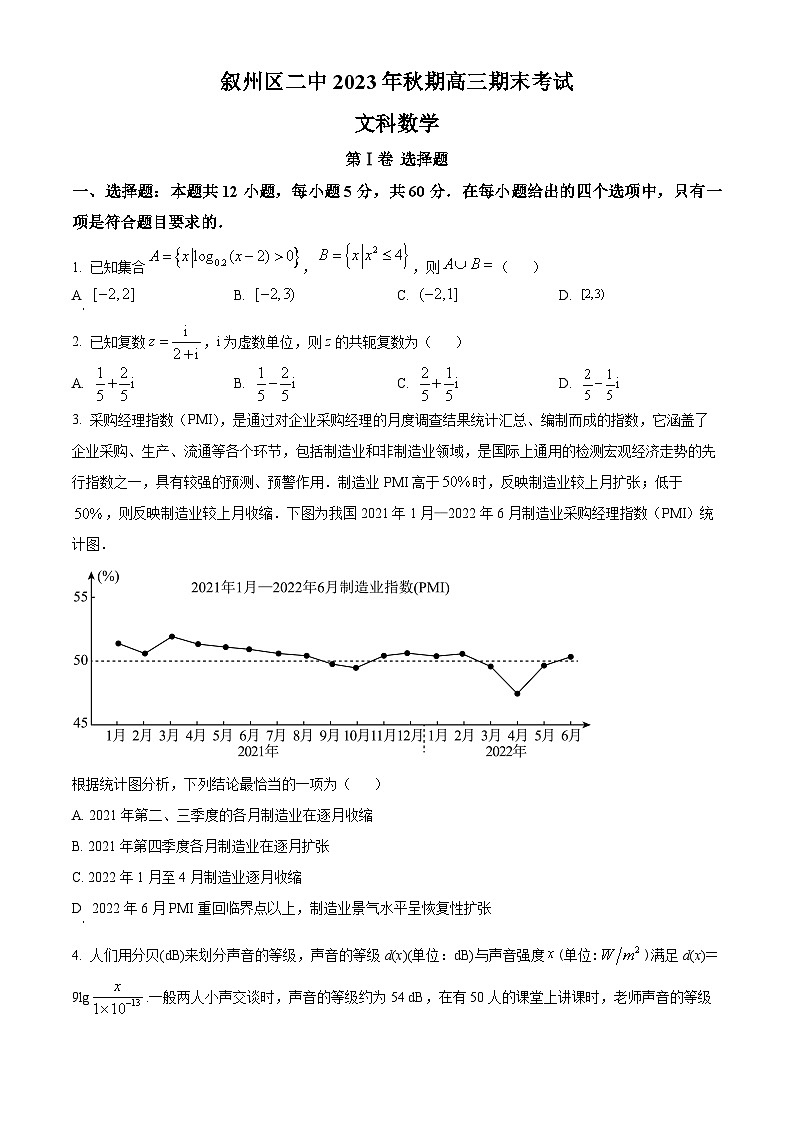
3. 采购经理指数（PMI），是通过对企业采购经理的月度调查结果统计汇总、编制而成的指数，它涵盖了企业采购、生产、流通等各个环节，包括制造业和非制造业领域，是国际上通用的检测宏观经济走势的先行指数之一，具有较强的预测、预警作用．制造业PMI高于时，反映制造业较上月扩张；低于，则反映制造业较上月收缩．下图为我国2021年1月—2022年6月制造业采购经理指数（PMI）统计图．
根据统计图分析，下列结论最恰当的一项为（ ）
A. 2021年第二、三季度的各月制造业在逐月收缩
B. 2021年第四季度各月制造业在逐月扩张
C. 2022年1月至4月制造业逐月收缩
D. 2022年6月PMI重回临界点以上，制造业景气水平呈恢复性扩张
【答案】D
【解析】
【分析】根据题意，将各个月的制造业指数与比较，即可得到答案.
【详解】对于A项，由统计图可以得到，只有9月份的制造业指数低于，故A项错误；
对于B项，由统计图可以得到，10月份的制造业指数低于，故B项错误；
对于C项，由统计图可以得到，1、2月份的制造业指数高于，故C项错误；
对于D项，由统计图可以得到，从4月份的制造业指数呈现上升趋势，且在2022年6月PMI超过，故D项正确.
故选：D.
4. 人们用分贝(dB)来划分声音的等级，声音的等级d(x)(单位：dB)与声音强度(单位:)满足d(x)＝9lg.一般两人小声交谈时，声音的等级约为54 dB，在有50人的课堂上讲课时，老师声音的等级约为63 dB，那么老师上课时声音强度约为一般两人小声交谈时声音强度的（ ）
A. 1倍B. 10倍
C. 100倍D. 1 000倍
【答案】B
【解析】
【分析】利用对数运算即可求解.
【详解】设老师上课时声音强度，一般两人小声交谈时声音强度分别为，
根据题意得＝，解得，，解得，所以
因此，老师上课时声音强度约为一般两人小声交谈时声音强度的10倍.
故选: B.
5. 已知直线的方程为，，则直线的倾斜角范围是（ ）
A. B.
C. D.
【答案】B
【解析】
【分析】计算，再考虑和两种情况，得到倾斜角范围.
【详解】，则，
设直线的倾斜角为，故，
所以当时，直线的倾斜角；
当时，直线的倾斜角；
综上所述：直线的倾斜角
故选：B
6. 已知，则（ ）
A. B. C. D.
【答案】D
【解析】
【分析】利用余弦的和差公式对原式进行展开，平方后再利用，，去进行整理可得.
【详解】因为，所以，平方后可得，整理得，所以.
故选：D.
7. 在正方体中，下列结论正确的是（ ）
A. 与所成的角为B. 与所成的角为
C. 与所成的角为D. 与所成的角为
【答案】A
【解析】
【分析】根据空间直线与直线夹角定义逐项判断即可.
【详解】
如图正方体中，设其棱长为1，
易知直线与直线平行，所以与所成的角即为与所成的角，
即为，而三角形为正三角形，所以，所以A正确；
同理与平行，与所成的角即为与所成角，即为，三角形为正三角形，所以，所以C错误；
因为，，，平面，平面，
所以平面，所以与所成的角即为，则B错误；
因为与平行，所以与所成角与与所成的角相等，
即为，三角形中，， ，
所以不为，则D错误；
故选：A
8. 若，，，则（ ）
A. B.
C. D.
【答案】D
【解析】
【分析】根据指数函数以及对数函数的性质，判断a,b,c的范围，即可比较大小，可得答案.
【详解】由函数为增函数可知，
由为增函数可得，由由为增函数可得，
，
，
故选:D
9. 设是定义域为R的奇函数，且.若，则（ ）
A. B. C. D.
【答案】C
【解析】
【分析】由题意利用函数的奇偶性和函数的递推关系即可求得的值.
【详解】由题意可得：，
而，
故.
故选：C.
【点睛】关键点点睛：本题主要考查了函数的奇偶性和函数的递推关系式，灵活利用所给的条件进行转化是解决本题的关键.
10. 若将函数的图像向右平移个单位长度后，与函数的图像重合，则的最小值是（ ）
A. B. C. D.
【答案】B
【解析】
【分析】先得到平移后的解析式，再由题中条件，列出等式，求出，即可得出结果.
【详解】将函数的图像向右平移个单位长度后得到函数的图像，
即，与函数的图像重合
即，
故
∴，
所以的最小值为.
故选：B.
11. 在四棱锥中，底面为等腰梯形，底面.若，，则这个四棱锥的外接球表面积为（ ）
A. B. C. D.
【答案】C
【解析】
【分析】先求得四棱锥的外接球的半径，再去求外接球表面积即可解决.
【详解】取BC中点E，连接EA、ED，取PC中点H，连接EH、BH，
等腰梯形中，，，
则有，则四边形为平行四边形，
则，又，则为等边三角形，
则，则△等边三角形
则，故点E为等腰梯形的外接圆圆心，
△中，，则
又底面，则底面，
又，
即，
故点H为四棱锥的外接球球心，
球半径
则四棱锥外接球表面积为
故选：C
12. 已知双曲线的右焦点与抛物线的焦点重合，过作与一条渐近线平行的直线，交另一条渐近线于点，交抛物线的准线于点，若三角形（为原点）的面积，则双曲线的方程为（ ）
A. B. C. D.
【答案】D
【解析】
【分析】由抛物线方程得出焦点坐标和准线方程，联立直线与渐近线方程得出的坐标，联立直线与准线方程得出的坐标，根据三角形的面积得出，再结合，，可解得结果.
【详解】由得，所以，
所以直线，抛物线的准线为：，
联立可得，所以，
联立可得，所以，
所以，
所以，所以，即，
又，，
所以，所以，所以，
所以双曲线的方程为.
故选：D.
【点睛】本题考查了抛物线和双曲线的几何性质，考查了三角形的面积，考查了运算求解能力，属于基础题.
第Ⅱ卷 非选择题
二、填空题：本题共4小题，每小题5分，共20分．
13. 已知实数满足，则的最大值为________．
【答案】11
【解析】
【分析】由约束条件作出可行域，化目标函数为直线方程的斜截式，数形结合得到最优解，把最优解的坐标代入目标函数得到答案.
【详解】由约束条件，画出可行域，如图：

令，化为斜截式方程得，
由图可知，当直线过点时，直线在轴上的截距最大.
由得，即.
所以点代入目标函数可得最大值，即最大值为.
故答案为：11.
14. 若直线与平行，则实数a的值是___________.
【答案】
【解析】
【分析】根据两直线平行得到，解得，再代入检验即可；
【详解】解：因为直线与平行，
所以，解得，
当时，直线与，两条直线重合，故舍去.
当时，直线与，符合题意.
故答案为：
15. 已知函数为上的奇函数，则实数______________________．
【答案】1
【解析】
【分析】利用奇函数的性质有，列方程求参数a即可.
【详解】由题设，
所以，可得.
故答案为：1
16. 在棱长为1的正方体中，点是对角线的动点（点与不重合），则下列结论正确的有__________.
①存在点，使得平面平面；
②分别是在平面，平面上的正投影图形的面积，存在点，使得；
③对任意的点，都有；
④对任意的点的面积都不等于.
【答案】①②③
【解析】
【分析】当直线交平面于点时，根据面面平行的判定定理即可判断①正确；设根据面积可解得即可判断②正确；利用线面垂直判定定理可证明当直线交平面于点时满足，可得③正确，由③可知当点是线段上靠近点的三等分点时，的面积等于，即④错误.
【详解】对于①，根据题意，连接，如下图所示：
由正方体性质可得，平面，平面，
所以可得平面，
同理可平面，又，且平面，
所以可得平面平面，
当直线交平面于点时，有平面，即①正确；
对于②，设，
则在平面上正投影图形的面积为，
在平面上的正投影图形的面积与在平面上的的面积相等，
即，
若，则可得，解得或，
又因为，所以可得，故存在点，使得，即②正确；
对于③，取的中点为，的中点为，连接交于点，如下图所示：
由正方形性质可知，，且，
又，平面，所以平面；
又，所以平面，可得，
由的中点为，所以可得即为线段的垂直平分线，
可知，即③正确；
对于④，利用正方体性质可得平面,平面,所以；
同理可得平面,平面,所以；
又，所以平面，
易知平面，所以；
结合③的结论即可得即为和的公垂线，即的高的最小值即为，
易知，，可得，
所以此时，即，
即的面积，
即当点是线段上靠近点的三等分点时，的面积等于，即④错误；
故答案为：①②③
【点睛】方法点睛：处理立体几何中动点问题时，往往利用面面平行、线面垂直等判定定理首先确定满足条件的动点位置，再利用几何体性质验证是否符合题意，即可求出最值或范围等问题.
三、解答题：共70分．解答应写出文字说明、证明过程或演算步骤．第17~21题为必考题，每个试题考生都必须作答．第22、23题为选考题，考生根据要求作答．
（一）必考题：共60分．
17. 已知函数
（1）求的单调递增区间；
（2）三角形的三边a，b，c满足，求的取值范围．
【答案】（1）
（2）
【解析】
【分析】（1）先利用倍角公式以及两角和差的正弦公式进行化简可得，然后根据函数的单调性即可求得的单调递增区间；
（2）根据余弦定理可求得，便可知的取值范围从而求得的取值范围.
【小问1详解】
解：由题意得：

当时，函数单调递增，解得：
的单调递增区间：
【小问2详解】
由可知
由余弦定理得：
故可知
∴
又
∴．
18. 近年来，我国新能源汽车技术水平不断进步、产品性能明显提升，产销规模连续六年位居世界首位.我国新能源汽车行业取得的成就离不开国家政策的支持，为支持我国新能源汽车行业发展，国家出台了一系列政策，其中《新能源汽车产业发展规划（2021－2035年）》提出，到2025年，新能源汽车新车销售量达到汽车新车销售总量的20％左右，力争经过15年的持续努力，我国新能源汽车核心技术达到国际先进水平，质量品牌具备较强国际竞争力.某汽车城从某天开始连续的营业天数x与新能源汽车销售总量y（单位：辆）的统计数据如表所示：
（1）已知可用线性回归模型拟合y与x的关系，请用相关系数加以说明（结果精确到0.001）；
（2）求y关于x的线性回归方程，并预测该汽车城连续营业130天的汽车销售总量.
参考数据：，，.
参考公式：相关系数，
线性回归方程中斜率与截距的最小二乘估计公式分别为，.
【答案】（1）答案见解析
（2），142辆
【解析】
【分析】（1）根据相关系数的计算公式代入数据即可求解，
（2）由最小二乘法的计算公式求解线性回归方程，即可代入求解.
【小问1详解】
，
，
，
，
则相关系数
，
因为y与x的相关系数近似为0.999，说明y与x的线性相关程度相当高，从而可用线性回归模型拟合y与x的关系.
【小问2详解】
由（1）得，
，
所以y关于x的线性回归方程为.
将代入，
得，
所以预测该汽车城连续营业130天的汽车销售总量为142辆.
19. 如图，平面平面，四边形为矩形，为正三角形，，为的中点.

（1）证明：平面平面；
（2）已知四棱锥的体积为，求点到平面的距离.
【答案】（1）证明见详解
（2）
【解析】
【分析】（1）利用平面几何知识结合已知条件可以证明，再利用面面垂直的性质进一步证明，
结合线面垂直、面面垂直的判定定理即得证.
（2）不妨设，则点到平面的距离即为的长度，结合附加条件四棱锥的体积为可以求得所有棱长，最终利用平面几何知识即可求解.
【小问1详解】
一方面：因为为正三角形且为的中点，所以（三线合一），
又因为平面平面且平面平面，并注意到平面，
所以由面面垂直性质可知平面，
又因为平面，
所以由线面垂直的性质可知；
另一方面：由题意不妨设，则，
因为为正三角形且为的中点，所以，，
所以，且，注意到与均为锐角，
所以，不妨设，

因为，
所以，即.
综合以上两方面有且，
注意到，平面，平面，
所有由线面垂直的判定有平面，
又因为平面，所以平面平面.
【小问2详解】
由（1）可知平面，则点到平面的距离即为的长度，
一方面梯形的面积为，，
所以有四棱锥的体积为，
另一方面由题可知四棱锥的体积为，
结合以上两方面有，解得，
因为，所以，由（1）可知，
所以，所以，
所以.
20. 动点P到定点F(0，1)的距离比它到直线的距离小1，设动点P的轨迹为曲线C，过点F的直线交曲线C于A、B两个不同的点，过点A、B分别作曲线C的切线，且二者相交于点M．
（1）求曲线C的方程；
（2）求证：；
（3）求△ ABM的面积的最小值．
【答案】（1）；
（2）见解析； （3）4．
【解析】
【分析】（1）利用定义判断出曲线为抛物线；
（2）设出点的坐标，利用导数分别求出过点的切线方程，求出交点的坐标为，联立直线和抛物线的方程，利用韦达定理算出，从而得到，利用向量可以计算，所以；
（3）利用焦半径公式和点到直线的距离可以求得，从而求得面积的最小值为．
【小问1详解】
解：由已知，动点在直线上方，
条件可转化为动点到定点的距离等于它到直线距离，
∴ 动点的轨迹是以为焦点，直线为准线的抛物线，
故其方程为．
【小问2详解】
证：设直线的方程为：，
由得：
，
设，
则，．
由得：
，
，
∴ 直线的方程为：① ，
直线的方程为：② ，
① －② 消y得：
，
即，
将代入① 得：
，
，
故，

，
．
【小问3详解】
解：由（2）知，点到的距离，
，
，
∴ 当时，的面积有最小值4．
【点睛】形如的抛物线，考虑其切线时可以利用导数去讨论．
21. 已知函数．
（1）求函数的极值；
（2）对于任意的，当时，不等式恒成立，求实数的取值范围．
【答案】（1）极小值为，极大值为；
（2）.
【解析】
【分析】（1）根据导数性质，结合极小值的定义进行求解即可；
（2）问题转化为恒成立，然后构造函数，利用导数判定其单调性即可.
【小问1详解】
由得，
令，则或，
令，则，
故当时，单调递增，
当时，单调递减，
当时，单调递增，
所以当时，函数有极小值点，极小值为；
当时，函数有极大值点，极大值为；
【小问2详解】
问题，时恒成立，
等价于恒成立，
构造函数，即，
即证函数上单调递减，
即在上恒成立，
由，
设，
因为，所以，所以函数单调递减，
故，因此.
【点睛】关键点睛：构造函数利用导数的性质进行求解是解题的关键，对于恒成立的问题可以用分离参数来处理.
（二）选考题，共10分．请考生在第22、23题中任选一题作答．如果多做，则按所做的第一题计分．
22. 以坐标原点为极点，x轴的正半轴为极轴建立极坐标系，圆C的极坐标方程为，直线l的参数方程为（t为参数）
（1）求圆C的半径以及圆心的直角坐标；
（2）若点直线l上，且在圆C内部（不含边界），求的取值范围．
【答案】（1）半径为4，
（2）
【解析】
【分析】（1）将圆的极坐标方程化为直角坐标方程，整理成标准方程，然后可得；
（2）直线参数方程代入目标函数，根据直线参数的几何意义，结合直线过圆心可得.
【小问1详解】
由圆C的极坐标方程得，
所以圆C的直角坐标方程为，即，
所以圆C的半径为4，圆心为．
【小问2详解】
设，
将代入，得．
根据直线l的参数方程中参数的几何意义可知，表示直线l上的点到点的距离，
又因为为圆C的圆心，
所以，即，即的取值范围是．
23. 已知函数的最小值为.
（1）求的值；
（2）若为正实数，且，求证：.
【答案】（1）；（2）证明见解析
【解析】
【分析】
（1）由题意，得到函数，利用分段函数和一次函数的性质求得函数的最小值，即可求解；
（2）由（1）可得，实数为正实数，且，代入利用基本不等式即可作出证明.
【详解】（1）由题意，函数，
当时，函数单调递减，所以；
当时，函数单调递减，所以；
当时，函数单调递增，所以，
综上可得，函数的最小值为，所以.
（2）由（1）可得，实数为正实数，且，
所以
.
当且仅当时等号成立，所以.从某天开始连续的营业天数x
10
20
30
40
50
新能源汽车销售总量y/辆
62
68
75
81
89