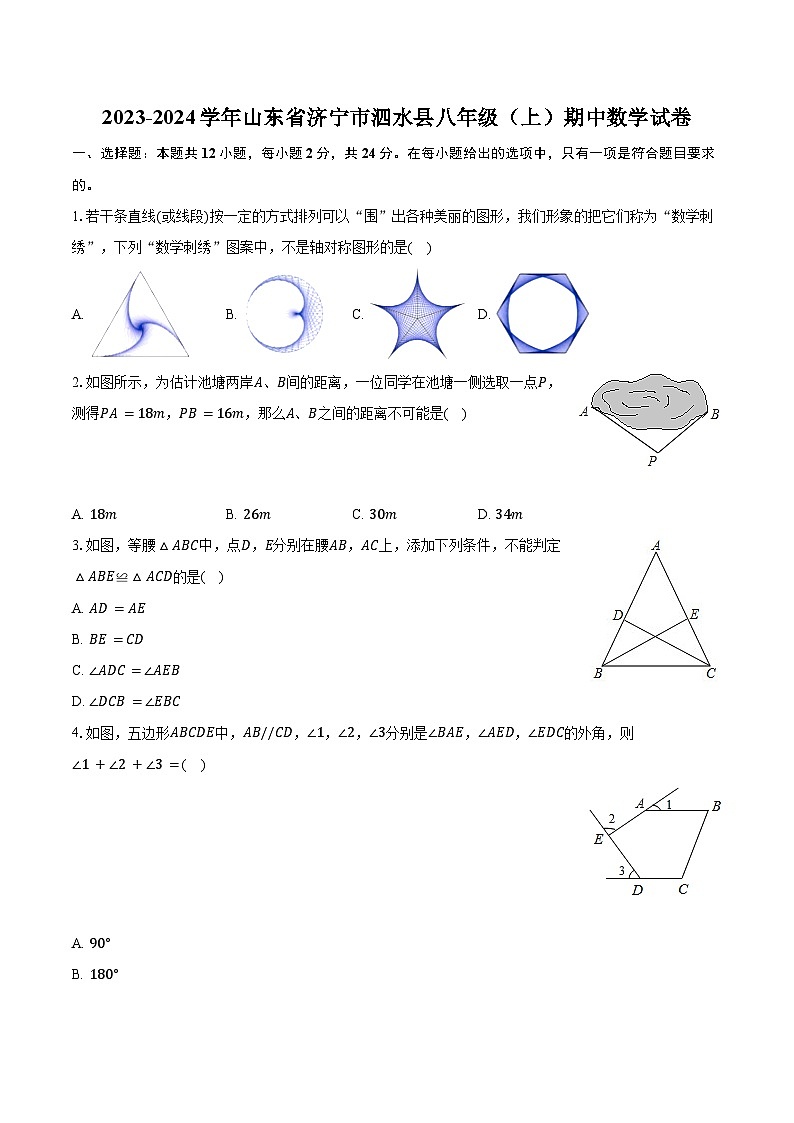
2023-2024学年山东省济宁市泗水县八年级（上）期中数学试卷（含解析）

这是一份2023-2024学年山东省济宁市泗水县八年级（上）期中数学试卷（含解析），共23页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

1.若干条直线(或线段)按一定的方式排列可以“围”出各种美丽的图形，我们形象的把它们称为“数学刺绣”，下列“数学刺绣”图案中，不是轴对称图形的是( )
A. B. C. D.
2.如图所示，为估计池塘两岸A、B间的距离，一位同学在池塘一侧选取一点P，测得PA=18m，PB=16m，那么A、B之间的距离不可能是( )
A. 18mB. 26mC. 30mD. 34m
3.如图，等腰△ABC中，点D，E分别在腰AB，AC上，添加下列条件，不能判定△ABE≌△ACD的是( )
A. AD=AE
B. BE=CD
C. ∠ADC=∠AEB
D. ∠DCB=∠EBC
4.如图，五边形ABCDE中，AB/​/CD，∠1，∠2，∠3分别是∠BAE，∠AED，∠EDC的外角，则∠1+∠2+∠3=( )
A. 90°
B. 180°
C. 120°
D. 270°
5.生活中，我们所见到的地面、墙面、服装面料等，常常是由一种或几种性质相同的图形拼接而成的.像这样的用形状、大小完全相同的一种或几种平面图形进行拼接，彼此之间不留空隙，不重叠地铺成一片，就是平面图形的镶嵌.如果选用两种几何图形镶嵌整个地面，下列哪种组合能镶嵌成一个平面图形.( )
A. 正三角形和正五边形B. 正方形和正六边形
C. 正方形和正八边形D. 正五边形和正九边形
6.如图，等腰直角三角形ABC中，∠BAC=90°，D是AC的中点，EC⊥BD于点E，交BA的延长线于点F，若BF=12，则△AFC的面积为( )
A. 16
B. 20
C. 48
D. 32
7.如图，Rt△ABC中，∠C=90°，∠B=30°，要求用圆规和直尺作图，把它分成两个三角形，其中一个三角形是等腰三角形．其作法错误的是( )
A. B.
C. D.
8.如图，在△ABC中，∠BAC=90°，AB=2AC，点D是线段AB的中点，将一块锐角为45°的直角三角板△ADE按如图放置，使直角三角板斜边的两个端点分别与A，D重合，连接BE，CE与AB交于点F.下列判断正确的有( )
①△ACE≌△DBE；
②BE⊥CE；
③△ADE与△ACE的面积相等．
A. ①②B. ①③C. ②③D. ①②③
9.如图，在△ABC中，∠BAC=80°，AB边的垂直平分线交AB于点D，交BC于点E，AC边的垂直平分线交AC于点F，交BC于点G，连接AE，AG.则∠EAG的度数为( )
A. 15°B. 20°C. 25°D. 30°
10.如图，甲、乙两位同学用n个完全相同的正六边形按如下方式拼成一圈后，使相邻的两个正六边形有公共顶点，设相邻两个正六边形外圈的夹角为x°，内圈的夹角为y°，中间会围成一个正n边形，关于n的值，甲的结果是n=5，乙的结果是n=3或4，则( )
A. 甲的结果正确B. 乙的结果正确
C. 甲、乙的结果合在一起才正确D. 甲、乙的结果合在一起也不正确
11.如图1，已知AB=AC，D为∠BAC的平分线上一点，连接BD、CD；如图2，已知AB=AC，D、E为∠BAC的平分线上两点，连接BD、CD、BE、CE；如图3，已知AB=AC，D、E、F为∠BAC的平分线上三点，连接BD、CD、BE、CE、BF、CF；…，依次规律，第n个图形中全等三角形的对数是( )
A. nB. 2n−1C. n(n+1)2D. 3(n+1)
12.如图，AC平分∠DAB，CE⊥AB于E，且AB−AD=2BE，下列结论正确的有个．( )
①AD=AE；
②∠DAB+∠DCB=180°；
③CD=CB；
④S△ACE−S△BCE=S△ADC；
⑤AB+AD=2AE．
A. 2个B. 3个C. 4个D. 5个
二、填空题：本题共6小题，每小题3分，共18分。
13.如图，∠B=40°，∠ACD=3∠B，那么∠A= ______度.
14.已知一个多边形的内角和比外角和多180°，则它的边数为 ．
15.如图，在Rt△ABC与Rt△DCB中，已知∠A=∠D=90°，请你添加一个条件(不添加字母和辅助线)，使Rt△ABC≌Rt△DCB，你添加的条件是______．
16.如图，在三角形纸片ABC中，AC=BC.把△ABC沿着AC翻折，点B落在点D处，连接BD.如果∠BAC=35°，则∠CBD的度数是______．
17.如图，AB=7cm，∠CAB=∠DBA=60°，AC=5cm，点P在线段AB上以2cm/s的速度由点A向点B运动，同时点Q在射线BD上运动，当点P运动结束时，点Q随之结束运动当点PO运动到某处时有△ACP与△BPQ全等，则Q的运动速度是______cm/s．
18.如图，△ABC中，AC⊥BC，D为BC边上的任意一点，连接AD，E为线段AD上的一个动点，过点E作EF⊥AB，垂足为F点.如果BC=10，AC=24，AB=26，则CE+EF的最小值为______．
三、解答题：本题共8小题，共58分。解答应写出文字说明，证明过程或演算步骤。
19.(本小题6分)
如图，点A，E，F，C在同一条直线上，AD//BC，AD=CB，AE=CF，求证：BE=DF．
20.(本小题6分)
阅读小明和小红的对话，解决下列问题．

(1)这个“多加的锐角”是______°.
(2)小明求的是几边形的内角和？
(3)若这是个正多边形，则这个正多边形的一个外角是多少度？
21.(本小题6分)
如图，在正方形网格上有一个△ABC．
(1)画出△ABC关于直线l对称的图形；
(2)在直线l上找一点P，使PB+PC的长最短．(不写作法，保留作图痕迹)
22.(本小题7分)
如图，已知线段AB与直线平行．
(1)作∠CAB的角平分线AE交直线CD于点E(尺规作图，保留作图痕迹，不写作法)；
(2)在(1)的条件下，若AE的中点为F，连接BF并延长交直线CD于点G，请用等式表示线段AB，AC，CG之间的数量关系：______．
23.(本小题7分)
如图，在△ABC中，∠A=80°，∠BDE=35°，BD平分∠ABC交AC于D，DE/​/AB交BC于E，求∠ABC和∠C的度数．
24.(本小题8分)
如图，△ABC为等边三角形，AE=CD，AD，BE相交于点P，BQ⊥AD于Q，PQ=5，PE=2．
(1)求证：AD=BE；
(2)求AD的长．
25.(本小题8分)
某校八年级(1)班数学兴趣小组在一次活动中进行了试验探究活动，请你和他们一起活动吧．
【探究与发现】
(1)如图1，AD是△ABC的中线，延长AD至点E，使ED=AD，连接BE，△ACD和△EBD全等吗？为什么？
【理解与运用】
(2)如图2，EP是△DEF的中线，若EF=5，DE=3，设EP=x，则x的取值范围是______．
26.(本小题10分)
在直线m上依次取互不重合的三个点D、A、E，在直线m上方有AB=AC，且满足∠BDA=∠AEC=∠BAC=α．
【积累经验】
(1)如图1，当α=90°时，猜想线段DE，BD，CE之间的数量关系是______；请说明理由；
【类比迁移】
(2)如图2，当0<α<180°时，问题(1)中结论是否仍然成立？如成立，请说明理由；若不成立，也请说明理由；
【拓展应用】
(3)如图3，在△ABC中，∠BAC是钝角，AB=AC，∠BAD<∠CAE，∠BDA=∠AEC=∠BAC，直线m与CB的延长线交于点F，若BC=3FB，△ABC的面积是12，直接写出△FBD与△ACE的面积之和．
答案和解析
1.【答案】A
解：B、C、D选项中的图形都能找到一条直线，使图形沿一条直线折叠，直线两旁的部分能够互相重合，所以是轴对称图形，不符合题意；
A选项中的图形不能找到一条直线，使图形沿一条直线折叠，直线两旁的部分能够互相重合，所以不是轴对称图形，符合题意；
故选：A．
根据轴对称图形的定义(如果一个图形沿着一条直线对折后两部分完全重合，那么这样的图形就叫做轴对称图形)对四个选项进行分析．
本题主要考查轴对称的知识，熟练掌握轴对称图形的定义是解题的关键．
2.【答案】D
解：根据三角形的三边关系可得：18−16即2∴A、B之间的距离不可能是34，
故选：D．
根据三角形的三边关系定理：三角形两边之和大于第三边，三角形的两边差小于第三边，可得18−16此题主要考查了三角形的三边关系，关键是掌握第三边的范围是：大于已知的两边的差，而小于两边的和．
3.【答案】B
【解析】【分析】
本题考查了全等三角形的判定：熟练掌握全等三角形的判定方法．选用哪一种方法，取决于题目中的已知条件．也考查了等腰三角形的性质．利用等腰三角形的性质得∠ABC=∠ACB，AB=AC，然后根据全等三角形的判定方法对各选项进行判断．
【解答】
解：∵△ABC为等腰三角形，
∴∠ABC=∠ACB，AB=AC，
∴当AD=AE时，则根据“SAS”可判断△ABE≌△ACD；
当∠AEB=∠ADC，则根据“AAS”可判断△ABE≌△ACD；
当∠DCB=∠EBC，则∠ABE=∠ACD，根据“ASA”可判断△ABE≌△ACD．
故选：B．
4.【答案】B
解：如图，∵AB/​/CD，
∴∠4+∠5=180°，
∵∠1+∠2+∠3+∠4+∠5=360°，
∴∠1+∠2+∠3=180°．
故选：B．
先利用平行线的性质得到∠4+∠5=180°，然后根据多边形的外角和为360°得到∠1+∠2+∠3+∠4+∠5=360°，从而得到∠1+∠2+∠3=180°．
本题考查了多边形内角与外角：多边形内角和为(n−2)⋅180 (n≥3)且n为整数)，外角和永远为360°.也考查了平行线的性质．
5.【答案】C
解：∵正三角形，正四边形，正五边形，正六边形，正八边形，正九边形的内角分别为：60°，90°，108°，120°，135°，140°．
而要用边长相同的两种正多边形材料组合铺设地面，能平整镶嵌必需这两个正多边形的内角的整数倍的和为360°，
∵90°+2×135°=360°，
∴正四边形和正八边形可以平整镶嵌．
故选：C．
先计算出正三角形，正四边形，正五边形，正六边形，正八边形，正九边形的内角，根据平整镶嵌的条件得到90°+2×135°=360°，由此得到正四边形和正八边形可以平整镶嵌．
本题考查了两个正多边形平面镶嵌的条件：这两个正多边形的内角的整数倍的和为360°.也考查了正多边形内角的计算方法．
6.【答案】A
解：∵CE⊥BD，
∴∠BEF=90°，
∵∠BAC=90°，
∴∠CAF=90°，
∴∠FAC=∠BAD=90°，∠ABD+∠F=90°，∠ACF+∠F=90°，
∴∠ABD=∠ACF，
在△ABD和△ACF中，
∠BAD=∠CAEAB=AC∠ABD=∠ACF，
∴△ABD≌△ACF(ASA)，
∴AD=AF，
∵AB=AC，D为AC中点，
∴AB=AC=2AD=2AF．
∵BF=AB+AF=12，
∴3AF=12，
∴AF=4，
∴AC=2AF=8，
∴△AFC的面积是12×AF×AC=12×4×8=16．
故选：A．
分析题意，可先得出∠ABD=∠ACF，根据ASA可证△ABD≌△ACF，推出AD=AF；然后可得出AB=AC=2AD=2AF，进而得到AF长，求出AC长；再根据三角形的面积公式得出△AFC的面积是12×AF×AC，代入求出即可．
此题考查的是全等三角形的判定与性质、等腰三角形的性质，掌握其性质定理是解决此题的关键．
7.【答案】B
解：A.由作法知AD=AC，
所以△ACD是等腰三角形，故选项A不符合题意；
B.由作法知所作图形是线段BC的垂直平分线，
所以不能推出△ACD和△ABD是等腰三角形，故选项B符合题意；
C. 由作法知，所作图形是线段AB的垂直平分线，
所以DA=DB，
所以△ABD是等腰三角形，故选项C不符合题意；
D.∠C=90°，∠B=30°，
∠BAC=60°，
由作法知AD是∠BAC的平分线，
所以∠BAD=30°=∠B，
所以DB=DA，
所以△ABD是等腰三角形，故选项D不符合题意；
故选B．
本题主要考查了尺规作图−作一条线段的垂直平分线、作一个角的平分线等，熟练掌握尺规作图的步骤，并能够准确识别对应的图形是解决问题的关键．
8.【答案】D
解：①∵点D是线段AB的中点，
∴BD=AD=12AB，
∵AB=2AC，
∴AC=12AB，
∴BD=AC，
∵△ADE为等腰直角三角形，
∴DE=AE，∠EDA=∠EAD=45°，
∴∠EDB=180°−45°=135°，
∵∠BAC=90°，
∴∠EAC=∠BAC+∠EAD=135°，
在△ACE和△DBE中，
DE=AE∠EDB=∠EACBD=AC，
∴△ACE≌△DBE(SAS)，故①正确，符合题意；
②∵△ACE≌△DBE(SAS)，
∴∠AEC=∠DEB，
∵∠AED=∠AEC+∠DEF=90°，
∴∠BEC=∠DEB+∠DEF=90°，
即BE⊥CE，故②正确，符合题意；
③∵△ACE≌△DBE(SAS)，
∴S△ACE=S△DBE，
∵BD=AD，
∴S△ADE=S△DBE，
∴S△ADE=S△ACE，故③正确，符合题意；
综上：正确的有①②③，
故选：D．
①根据点D是线段AB的中点，得出BD=AD=12AB，根据等腰直角三角形的性质，推出DE=AE，∠EDB=∠EAC=135°，即可求证△ACE≌△DBE(SAS)；②根据全等的性质得出∠AEC=∠DEB，推出∠BEC=∠DEB+∠DEF=90°，即BE⊥CE；③根据全等的性质得出S△ACE=S△DBE，根据三角形中线的性质得出S△ADE=S△DBE，则S△ADE=S△ACE．
本题主要考查了全等三角形的判定和性质，等腰直角三角形的性质，三角形中线的性质，解题的关键是掌握全等三角形对应角相等，对应边相等，面积相等；三角形中线将三角形面积平均分为两份．
9.【答案】B
解：∵AB边的垂直平分线交AB于点D，AC边的垂直平分线交AC于点F，
∴AG=CG，AE=BE，
∴∠C=∠CAG，∠B=∠BAE，
∴∠BAE+∠CAG=∠B+∠C=180°−∠BAC=100°，
∴∠EAG=∠BAE+∠CAG−∠BAC=100°−80°=20°，
故选：B．
根据线段垂直平分线的性质和等腰三角形的性质即可得到结论．
此题考查了线段垂直平分线的性质，等腰三角形的性质，正确的识别图形是解题的关键．
10.【答案】D
解：∵正六边形的一个内角为(6−2)×180°6=120°，
∴x+y=360°−2×120°=120°，
∵y°为正n边形的一个内角为度数，
∴y=(n−2)×180°n，
当n=3时，y=60°，则x=60°，
当n=4时，y=90°，则x=30°，
当n=5时，y=108°，则x=12°，
当n=6时，y=120°，x=0°，
则n的值为3或4或5或6．
故选：D．
正六边形的一个内角为120°，根据周角的定义有，x+y=360°−2×120°=120°，得y=(n−2)×180°n，再讨论即可得n的值．
本题考查了多边形的内角与外角．注意求正多边形的内角常常转化到求外角来计算．
11.【答案】C
解：由题知，第1个图形中全等三角形的对数为：1；
第2个图形中全等三角形的对数为：1+2=3；
第3个图形中全等三角形的对数为：1+2+3=6；
第4个图形中全等三角形的对数为：1+2+3+4=10；
...
第n个图形中全等三角形的对数为：1+2+3+4+...+n=n(n+1)2；
故选：C．
根据图形得出当有1点D时，有1对全等三角形；当有2点D、E时，有3对全等三角形；当有3点D、E、F时，有6对全等三角形；根据以上结果得出当有n个点时，可求得有12n(n+1)对全等三角形．
本题主要考查全等三角形的判定，关键是根据已知图形得出规律，题目比较典型，但有一定的难度．
12.【答案】C
解：在AE上取点F，使EF=BE，连接CF，
∵AB=AD+2BE=AF+EF+BE，EF=BE，
∴AB=AD+2BE=AF+2BE，
∴AD=AF，且AF∴AD∴AB+AD=AF+EF+BE+AD=2AF+2EF=2(AF+EF)=2AE，故⑤正确；
∵AC平分∠DAB，
∴∠DAC=∠FAC，
∵AD=AF，AC=AC，
∴△ACD≌△ACF(SAS)，
∴∠ADC=∠AFC．
∵CE垂直平分BF，
∴CF=CB，
∴∠CFB=∠B．
又∵∠AFC+∠CFB=180°，
∴∠ADC+∠B=180°，
∴∠DAB+∠DCB=360−(∠ADC+∠B)=180°，故②正确；
由②知，△ACD≌△ACF，
∴CD=CF，
又∵CF=CB，
∴CD=CB，故③正确；
∵CF=CB，CE=CE，
∴Rt△CEF≌Rt△CEB(HL)，
∴S△ACE−S△BCE=S△ACE−S△FCE=S△ACF，
又∵△ACD≌△ACF，
∴S△ACF=S△ADC，
∴S△ACE−S△BCE=S△ADC，故④正确，
∴结论正确的有②③④⑤，共4个，
故选：C．
在AE取点F，使EF=BE，连接CF，利用已知条件AB=AD+2BE，可得AD=AF，进而可以判断①；证出2AE=AB+AD，进而可以判断⑤；先由SAS证明△ACD≌△ACF，得出∠ADC=∠AFC；再根据线段垂直平分线、等腰三角形的性质得出∠CFB=∠B；然后由邻补角定义及四边形的内角和定理得出∠DAB+∠DCB=180°，可以判断②；根据全等三角形的对应边相等得出CD=CF，根据线段垂直平分线的性质性质得出CF=CB，从而CD=CB，进而可以判断③；由于△CEF≌△CEB，△ACD≌△ACF，根据全等三角形的面积相等易证S△ACE−S△BCE=S△ADC进而可以判断④，即可解决问题．
本题是三角形综合题，考查了角平分线性质，全等三角形的性质和判定，等腰三角形的性质，四边形的内角和定理，邻补角定义等知识点的应用，正确作辅助线是解此题的关键，综合性比较强．
13.【答案】80
解：∵∠B=40°，∠ACD=3∠B，∠ACD=∠A+∠B
∴∠A=∠ACD−∠B=3∠B−∠B=2∠B=80°，
故答案为：80．
根据三角形的外角的性质可得∠ACD=∠A+∠B，结合已知条件，即可求解．
本题考查了三角形的外角的性质，熟练掌握三角形的外角的性质是解题的关键．
14.【答案】5
解：设这个多边形是n边形，
根据题意得，(n−2)⋅180°=360°+180°，
解得n=5．
故答案为：5．
根据多边形的内角和公式(n−2)⋅180°与外角和定理列出方程，然后求解即可．
本题考查了多边形的内角和公式与外角和定理，多边形的外角和与边数无关，任何多边形的外角和都是360°．
15.【答案】AB=DC(答案不唯一)
【解析】此题主要考查了全等三角形的判定和性质的应用，要熟练掌握，解答此题的关键是要明确：①判定定理1：SSS−三条边分别对应相等的两个三角形全等．②判定定理2：SAS−两边及其夹角分别对应相等的两个三角形全等．③判定定理3：ASA−两角及其夹边分别对应相等的两个三角形全等．④判定定理4：AAS−两角及其中一个角的对边对应相等的两个三角形全等．⑤判定定理5：HL−斜边与直角边对应相等的两个直角三角形全等．
根据斜边与直角边对应相等的两个直角三角形全等，使Rt△ABC≌Rt△DCB，添加的条件是：AB=DC．
解：∵斜边与直角边对应相等的两个直角三角形全等，
∴在Rt△ABC与Rt△DCB中，已知∠A=∠D=90°，BC=CB，使Rt△ABC≌Rt△DCB，添加的条件是：AB=DC．
故答案为：AB=DC(答案不唯一)．
16.【答案】20°
解：∵AC=BC，∠BAC=35°，
∵∠ABC=∠BAC=35°，
由折叠的性质可得：∠CAD=∠BAC=35°，AB=AD，
∴∠BAD=∠CAD+∠BAC=70°，
∴∠ABD=12(180°−∠BAD)=55°，
∴∠CBD=∠ABD−∠ABC=20°．
故答案为：20°．
由AC=BC，∠BAC=35°，根据等边对等角的性质，即可求得∠ABC的度数，又由折叠的性质，求得∠ABD的度数，继而求得∠CBD的度数．
此题考查了折叠的性质与等腰三角形的性质．此题注意折叠中的对应关系，注意数形结合思想的应用．
17.【答案】2或207
解：设点Q在射线BD上运动速度为x cm/s，它们运动的时间为t s，
①若△ACP≌△BPQ，
则AC=BP，AP=BQ，
∴5=7−2t，2t=xt，
解得：x=2，t=1；
②若△ACP≌△BQP，
则AC=BQ，AP=BP，
∴5=xt，2t=7−2t
解得：x=207，t=74．
综上，Q的运动速度是2cm/s或207cm/s，
故答案为：2或207．
分两种情况：①△ACP≌△BPQ时AC=BP，AP=BQ，②△ACP≌△BQP时AC=BQ，AP=BP，建立方程组求得答案即可．
此题考查全等三角形的性质，关键是了解全等三角形的对应角相等，对应边相等，解决此题的关键是注意分类讨论．
18.【答案】12013
解：过C作CF⊥AB于F，交AD于E，
则CE+EF的最小值为CF．
∵BC=0，AC=24，AB=26，
∴12AB⋅CF=12BC⋅AC，
∴CF=AC⋅BCAB=24×1026=12013，
即CE+EF的最小值为：12013．
故答案为：12013．
过C作CF⊥AB于F，交AD于E.则CE+EF的最小值为CF，利用三角形等面积法12AB⋅CF=12BC⋅AC，求出CF即为CE+EF的最小值．
本题考查了轴对称−最短路线问题，正确运用三角形等面积法是解题的关键．
19.【答案】证明：∵AD/​/BC，
∴∠A=∠C．
∵AE=FC，
∴AF=CE．
在△ADF和△CBE中，
AD=CB∠A=∠CAF=CE，
∴△ADF≌△CBE(SAS)．
∴BE=DF．
【解析】根据平行线的性质得到∠A=∠C.根据线段的和差得到AF=CE.推出△ADF≌△CBE(SAS).根据全等三角形的性质即可得到结论．
本题考查了全等三角形的判定及性质；解题关键是找准依据，从题中筛选条件，利用边角边判定进行解答．
20.【答案】30
解：(1)12边形的内角和为(12−2)×180°=1800°，而13边形的内角和为(13−2)×180°=1980°，
由于小红说：“多边形的内角和不可能是1830°，你一定是多加了一个锐角”，所以这个“多加的锐角是1830°−1800°=30°，
故答案为：30；
(2)设这个多边形为n边形，由题意得：
(n−2)×180°=1800°，
解得：n=12；
答：小明求的是12边形的内角和；
(3)正12边形的每一个外角都相等，而多边形的外角和始终为360°，
所以每一个外角为360°12=30°，
答：这个正多边形的每一个外角为30°
(1)根据多边形的内角和的公式进行估算即可；
(2)根据对话和多边形的内角和公式列方程求解即可；
(3)根据正多边形外角和为360°，而每一个外角都相等进行计算即可；
本题主要考查多边形的内角和和外角和，掌握多边形内角和的计算方法以及多边形的性质是正确解答的前提．
21.【答案】解：(1)如图所示，△AB′C′即为所求作的三角形；
(2)如图所示，点P即为所求．

【解析】(1)根据网格结构找出点B、C关于直线l的对称点B′、C′的位置，然后顺次连接即可；
(2)根据轴对称确定最短路线，连接B′C，与对称轴l的交点即为所求点P．
本题考查了利用轴对称变换作图，凡是涉及最短距离的问题，一般要考虑线段的性质定理，结合轴对称变换来解决，多数情况要作点关于某直线的对称点．
22.【答案】CG+AC=AB
解：(1)AE就是∠CAB的角平分线；
(2)∵AE是∠CAB的角平分线，
∴∠CAE=∠EAB．
∵AB/​/CD，
∴∠CEA=∠EAB．
∴∠CAE=∠CEA．
∴AC=CE．
∵AE的中点为F，
∴AF=FE．
在△GFE和△BFA中，
∠GEA=∠EABAF=EF∠AFB=∠GFE，
∴△GFE≌△BFA(ASA)．
∴GE=AB．
∴CG+CE=CG+AC=AB．
(1)利用尺规作图作出角的平分线；
(2)利用等腰三角形的判定和性质先说明AC=CE，再利用“ASA”说明△GFE≌△BFA，最后利用线段的和差及全等三角形的性质得结论．
本题主要考查了平行线的性质，掌握等腰三角形的性质和判定、全等三角形的性质和判定是解决本题的关键．
23.【答案】解：∵DE//AB，
∴∠ABD=∠BDE=35°
∵BD平分∠ABC，
∴∠ABC=2∠ABD=70°，
∵∠A+∠C+∠ABC=180°
∴∠C=180°−∠A−∠ABC
=180°−80°−70°
=30°．

【解析】先利用三角形的内角和定理求出∠ABC，再利用角平分线的定义和平行线的性质得结论．
本题主要考查了三角形的内角和定理，掌握“三角形的内角和是180°”、“两直线平行，内错角相等”及角平分线的性质是解决本题的关键．
24.【答案】(1)证明：∵△ABC为等边三角形，
∴∠BAC=∠C=60°，AB=AC，
又∵AE=CD，
∴△ABE≌△CAD(SAS)，
∴BE=AD；
(2)解：∵△ABE≌△CAD，
∴∠ABE=∠CAD，
∵∠BPQ=∠BAP+∠ABE=∠BAP+∠PAE=∠BAC=60°，
又∵BQ⊥PQ，
∴∠PBQ=30°．
∴PB=2PQ=10，
∴BE=PB+PE=12．
∴AD=BE=12．
【解析】(1)根据SAS证明△ABE与△CAD全等即可；
(2)根据全等三角形的性质得出∠ABE=∠CAD，求出∠PBQ=30°，进而由直角三角形的性质解答即可．
本题考查了全等三角形的判定与性质、含30度角的直角三角形，等边三角形的性质，证明△ABE≌△CAD是解题的关键．
25.【答案】1解：(1)△ACD≌△EBD，
理由：∵AD是△ABC的中线，
∴CD=BD，
在△ACD和△EBD中，
AD=ED∠ADC=∠EDBCD=BD，
∴△ACD≌△EBD(SAS)．
(2)如图2，延长EP到点G，使GP=EP，连接FG，则EG=2EP=2x，
∵EP是△DEF的中线，
∴FP=DP，
在△FPG和△DPE中，
GP=EP∠FPG=∠DPEFP=DP，
∴△FPG≌△DPE(SAS)，
∴FG=DE=3，
∵EF−FG∴5−3<2x<5+3，
∴1故答案为：1(1)由D是△ABC的中线得CD=BD，而∠ADC=∠EDB，CD=BD，即可根据“SAS”证明△ACD≌△EBD；
(2)延长EP到点G，使GP=EP，连接FG，则EG=2EP=2x，可证明△FPG≌△DPE，得FG=DE=3，根据三角形的三边关系得EF−FG此题重点考查全等三角形的判定与性质、三角形的三边关系、不等式的应用等知识，正确地作出辅助线构造全等三角形是解题的关键．
26.【答案】DE=BD+CE
解：(1)DE=BD+CE，理由如下，
∵∠BDA=∠BAC=∠AEC=90°，
∴∠BAD+∠EAC=∠BAD+∠DBA=90°，
∴∠DBA=∠EAC，
∵AB=AC，
∴△DBA≌△EAC(AAS)，
∴AD=CE，BD=AE，
∴DE=AD+AE=BD+CE，
故答案为：DE=BD+CE．
(2)DE=BD+CE仍然成立，理由如下，
∵∠BDA=∠BAC=∠AEC=α，
∴∠BAD+∠EAC=∠BAD+∠DBA=180°−α，
∴∠DBA=∠EAC，
∵AB=AC，
∴△DBA≌△EAC(AAS)，
∴BD=AE，AD=CE，
∴DE=AD+AE=BD+CE；
(3)解：∵∠BAD<∠CAE，∠BDA=∠AEC=∠BAC，
∴∠CAE=∠ABD，
在△ABD和△CAE中，
∠ABD=∠CAE∠BDA=∠CEAAB=AC，
∴△ABD≌△CAE(AAS)，
∴S△ABD=S△CAE，
设△ABC的底边BC上的高为ℎ，则△ABF的底边BF上的高为ℎ，
∴S△ABC=12BC⋅ℎ=12，S△ABF=12BF⋅ℎ，
∵BC=3BF，
∴S△ABF=4，
∵S△ABF=S△BDF+S△ABD=S△FBD+S△ACE=4，
∴△FBD与△ACE的面积之和为4．
(1)由∠BDA=∠BAC=∠AEC=90°得到∠BAD+∠EAC=∠BAD+∠DBA=90°，进而得到∠DBA=∠EAC，然后结合AB=AC得证△DBA≌△EAC，最后得到DE=BD+CE；
(2)由∠BDA=∠BAC=∠AEC=α得到∠BAD+∠EAC=∠BAD+∠DBA=180°−α，进而得到∠DBA=∠EAC，然后结合AB=AC得证△DBA≌△EAC，最后得到DE=BD+CE；
(3)由∠BAD>∠CAE，∠BDA=∠AEC=∠BAC，得出∠CAE=∠ABD，由AAS证得△ADB≌△CAE，得出S△ABD=S△CEA，再由不同底等高的两个三角形的面积之比等于底的比，得出S△ABF即可得出结果．
本题是三角形综合题，考查了全等三角形的判定与性质、直角三角形的性质，三角形的面积，解题的关键是熟练掌握全等三角形的判定与性质．