



云南省昆明市官渡区2023-2024学年七年级上学期期末数学试题(原卷+解析)
展开(全卷三个大题,共24个小题,共8页;满分100分,考试用时120分钟)
注意事项:
1.本卷为试题卷.考生必须在答题卡上解题作答.答案应书写在答题卡的相应位置上,在试题卷、草稿纸上作答无效.
2.考试结束后,请将试题卷和答题卡一并交回.
一、选择题(本大题共12小题,每小题只有一个正确选项,每小题3分,共36分)
1. 中国是世界上最早提出和采用“正负数表示相反意义的量”的国家,关于正负数的记载最早见于公元一世纪的中国数学著作《九章算术》中,比欧洲早一千余年.如果将“支出45元”记作“元”,那么“收入25元”记作( )
A. 元B. 元C. 元D. 元
【答案】C
【解析】
【分析】本题考查了正负数的实际应用,熟知正负数代表相反意义的量是解本题的关键.根据正负数代表相反意义的量即可解答.
【详解】解:“支出45元”记作“元”,那么“收入25元”记作元,
故选:C
2. 年月日,丽江至香格里拉铁路正式开通运营,至此云南迪庆藏族自治州结束了不通铁路的历史.丽香铁路为全国一级单线电气化铁路,全长米,将数据用科学记数法表示为( )
A. B. C. D.
【答案】B
【解析】
【分析】本题考查科学记数法,根据将一个数写成的形式叫科学记数法直接求解即可得到答案;
【详解】解:由题意可得,
,
故选:B.
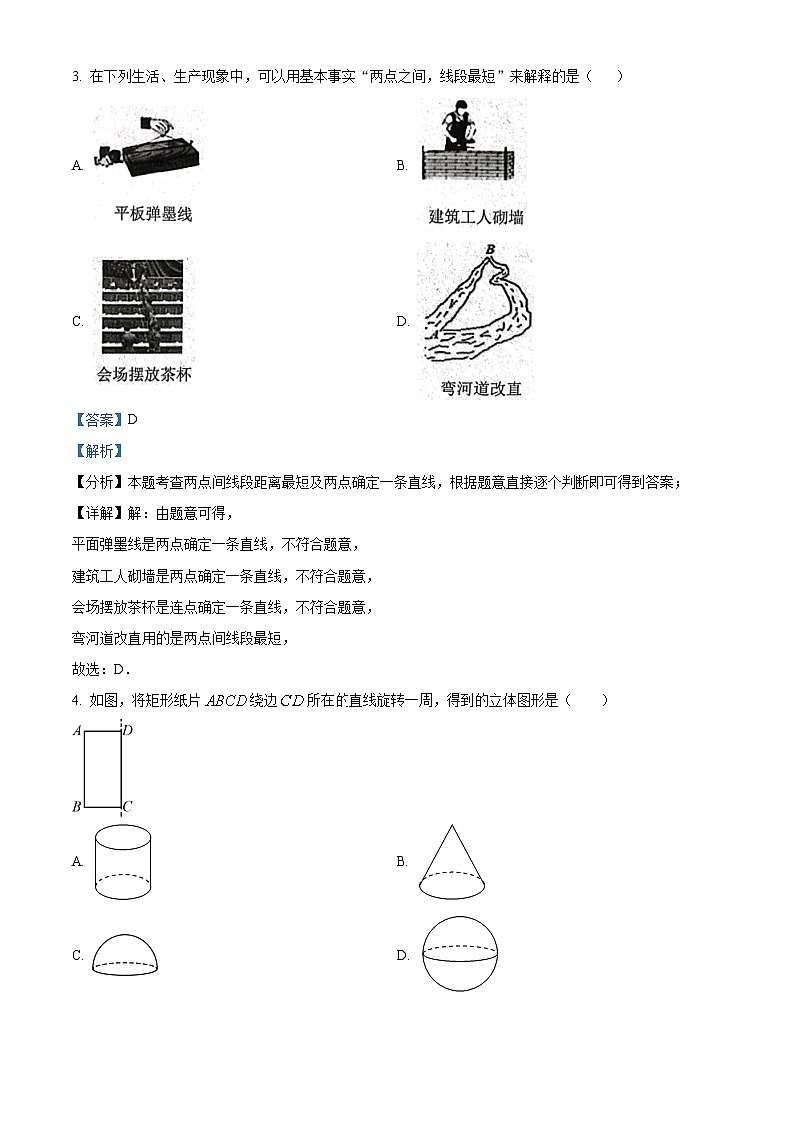
3. 在下列生活、生产现象中,可以用基本事实“两点之间,线段最短”来解释的是( )
A. B.
C. D.
【答案】D
【解析】
【分析】本题考查两点间线段距离最短及两点确定一条直线,根据题意直接逐个判断即可得到答案;
【详解】解:由题意可得,
平面弹墨线是两点确定一条直线,不符合题意,
建筑工人砌墙是两点确定一条直线,不符合题意,
会场摆放茶杯是连点确定一条直线,不符合题意,
弯河道改直用的是两点间线段最短,
故选:D.
4. 如图,将矩形纸片绕边所在直线旋转一周,得到的立体图形是( )
A. B.
C. D.
【答案】A
【解析】
【分析】根据矩形绕一边旋转一周得到圆柱体示来解答.
【详解】解:矩形纸片绕边所在的直线旋转一周,得到的立体图形是圆柱体.
故选:A.
【点睛】本题考查了点、线、面、体,熟练掌握“面动成体”得到的几何体的形状是解题的关键.
5. 在有理数,,,,,,中,负分数有( )
A. 3个B. 4个C. 5个D. 6个
【答案】A
【解析】
【分析】本题考查了有理数的分类,牢记有理数的分类是解题的关键.
【详解】解:,,是负分数,共个,
故选:A.
6. 下列等式变形正确的是( )
A. 若,则B. 若,则
C. 若,则D. 若,则
【答案】D
【解析】
【分析】本题考查了等式的基本性质,正确掌握等式的性质是解题的关键.等式的基本性质1是等式的两边都加上(或减去)同一个整式,所得的结果仍是等式;等式的基本性质2是等式的两边都乘以(或除以)同一个数(除数不能为0),所得的结果仍是等式.根据等式的性质逐项分析即可.
【详解】解: A.等式两边同时加上y,得,故选项A错误;
B.等式两边同时乘4,得,故选项B错误;
C.等式两边同时除以a,但未说明,故选项C错误;
D.等式两边同时乘,得,故选项D正确.
故选:D.
7. 有理数在数轴的位置如图所示,下列说法正确的是( )
A. B. C. D.
【答案】B
【解析】
【分析】本题考查根据数轴上点判断式子与0的关系,根据数轴得到,,结合加减法则求解即可得到答案;
【详解】解:由数轴可得,
,,故B正确,
∴,,,故A、C、D错误,
故选:B.
8. 下列说法正确的是( )
A. 是整式B. 0是单项式
C. 的系数是D. 是一次三项式
【答案】B
【解析】
【分析】本题考查单项式,多项式,整式的定义及系数次数的判断,根据单项式,多项式的定义,系数,次数的概念直接逐个判断即可得到答案
【详解】解:不是整式,故A错误,不符合题意,
0是单项式,故B正确,符合题意,
系数是,故C错误,不符合题意,
是二次三项式,故D错误,不符合题意,
故选:B.
9. 如图,某动物园的大象馆A位于大门O的北偏东的方向,海洋世界B位于大门O的南偏东的方向,那么的大小为( )
A. B. C. D.
【答案】C
【解析】
【分析】本题主要考查了方向角,解题的关键是根据题意找出图中角的度数.利用方向角的定义求解即可.
【详解】解:∵某动物园的大象馆A位于大门O的北偏东的方向,海洋世界B位于大门O的南偏东的方向,
∴,
故选:C.
10. 若与是同类项,则值为( )
A. B. C. 1D. 2
【答案】C
【解析】
【分析】本题考查了同类项的定义,掌握两个相同是解题关键.含有相同的字母,并且相同字母的指数也相同的两个单项式是同类项.
【详解】解:∵与是同类项,
∴,,
解得:,,
∴.
故选:C.
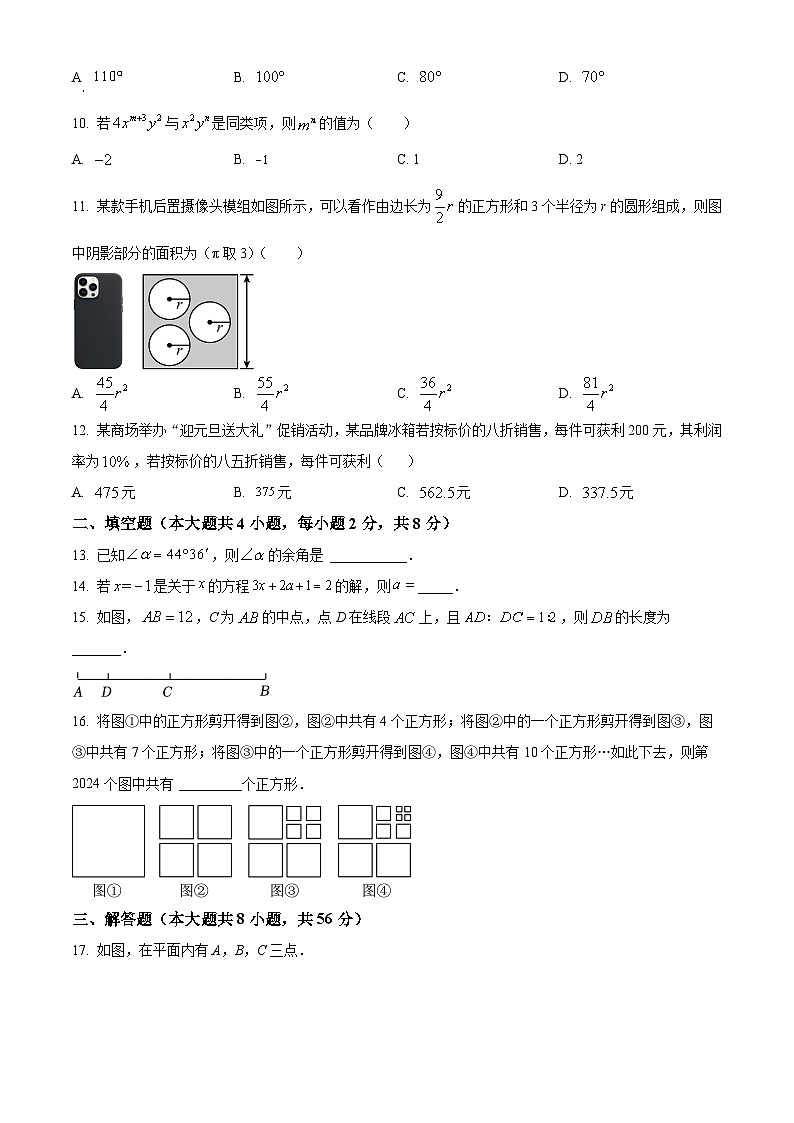
11. 某款手机后置摄像头模组如图所示,可以看作由边长为的正方形和3个半径为r的圆形组成,则图中阴影部分的面积为(π取3)( )
A. B. C. D.
【答案】A
【解析】
【分析】本题考查了圆的面积、正方形的面积,关键是计算正确.图中阴影部分的面积个正方形的面积个圆的面积.
【详解】解:正方形的面积,
3个圆的面积,
图中阴影部分的面积,
故选:A
12. 某商场举办“迎元旦送大礼”促销活动,某品牌冰箱若按标价的八折销售,每件可获利200元,其利润率为,若按标价的八五折销售,每件可获利( )
A. 元B. 元C. 元D. 元
【答案】D
【解析】
【分析】利用进价利润利润率可求出该品牌冰箱的进价,设该品牌冰箱的标价为x元,根据“若按标价的八折销售,每件可获利元”,即可得出关于x的一元一次方程,解之即可求出x的值,再将其代入中即可求出结论.
【详解】解:该品牌冰箱的进价为(元).
设该品牌冰箱的标价为x元,
依题意得:,
解得:,
∴(元).
故选:D.
【点睛】本题考查了一元一次方程的运用,找准等量关系,正确列出一元一次方程是解题的关键.
二、填空题(本大题共4小题,每小题2分,共8分)
13. 已知,则的余角是 ___________.
【答案】
【解析】
【分析】本题主要考查了求一个角的余角的度数,根据度数之和为90度的两个角互余进行求解即可.
【详解】解:∵,
∴的余角是
故答案为:.
14. 若是关于的方程的解,则_____.
【答案】2
【解析】
【分析】本题主要考查的是一元一次方程的解和解一元一次方程,依据题意得到关于的方程是解题的关键.将方程的解代入得到关于的一元一次方程,然后解关于的方程即可.
【详解】解:将代关于的方程,得:,
解得:.
故答案为:2
15. 如图,,C为的中点,点D在线段上,且,则的长度为 _______.
【答案】10
【解析】
【分析】本题主要考查了与线段中点有关的线段和差计算,先由线段中点得到,再求出,则.
【详解】解:∵,C为的中点,
∴,
∵点D在线段上,且,
∴,
∴,
故答案为:10.
16. 将图①中的正方形剪开得到图②,图②中共有4个正方形;将图②中的一个正方形剪开得到图③,图③中共有7个正方形;将图③中的一个正方形剪开得到图④,图④中共有10个正方形…如此下去,则第2024个图中共有 _________个正方形.
【答案】6070
【解析】
【分析】本题主要考查了图形规律探索,结合题意确定图形变化规律是解题关键.根据图①、图②、图③、图④中正方形个数变化情况,可知第个图中,正方形有个,即可获得答案.
【详解】解:第1个图中,正方形有1个,
第2个图中,正方形有个,
第3个图中,正方形有个,
第4个图中,正方形有个,
……
∴第个图中,正方形有个,
∴第2024个图中,正方形有:个.
故答案为:6070.
三、解答题(本大题共8小题,共56分)
17. 如图,平面内有A,B,C三点.
(1)画直线,射线,线段;
(2)在线段上任取一点D(不同于B,C),连接,并延长至E,使;
(3)数一数,此时图中线段共有______条.
【答案】(1)见解析 (2)见解析
(3)8
【解析】
【分析】(1)依据直线、射线、线段的定义,即可得到直线,射线,线段;
(2)依据在线段上任取一点D(不同于B,C),连接线段即可;
(3)根据图中的线段为,即可得到图中线段的条数.
【小问1详解】
如图,直线,射线,线段即为所求;
【小问2详解】
如图,线段和线段即为所求;
【小问3详解】
由题可得,图中线段的条数为,共8个,
故答案为:8.
【点睛】本题主要考查了直线、射线、线段的定义,熟练掌握各定义是解题的关键.
18. 计算:
(1);
(2);
(3).
【答案】(1);
(2);
(3).
【解析】
【分析】()根据有理数的加减运算法则进行计算即可得到结果;
()先把除法转化成乘法,再利用乘法分配律进行计算即可得到结果;
()先算乘方,再算乘除,最后进行加减运算即可得到结果;
本题考查了有理数的运算,掌握有理数的运算法则和运算律是解题的关键.
【小问1详解】
解:
,
;
【小问2详解】
解:
,
,
,
,
;
【小问3详解】
解:
,
,
.
19. 先化简,再求值:,其中,.
【答案】;
【解析】
【分析】本题主要考查了整式化简求值,解题的关键是熟练掌握去括号法则和合并同类项法则,注意括号前面为负号时,将负号和括号去掉后,括号里每一项的符号要发生改变.
【详解】解:
,
当,时,原式.
20. 解方程:
(1);
(2).
【答案】(1)
(2)
【解析】
【分析】本题主要考查了解一元一次方程,解题的关键是熟练掌握解一元一次方程的基本步骤,“先去分母、再去括号,然后移项合并同类项,最后系数化为1”,准确计算.
(1)先去括号,然后移项合并同类项,最后系数化为1;
(2)先去分母、再去括号,然后移项合并同类项,最后系数化为1.
【小问1详解】
解:
去括号得:
移项、合并同类项得:,
系数化1得:.
【小问2详解】
解:,
去分母得:,
去括号得:,
移项、合并同类项得:,
系数化1得:.
21. 某班数学活动小组的同学用纸板制作长方体包装盒,其平面展开图和相关尺寸如图所示,其中阴影部分为内部粘贴角料.(单位:)请结合图形解决下列问题:
(1)此长方体包装盒的体积为 用含,的式子表示)
(2)此长方体包装盒的表面积(不含内部粘贴角料)为 ;(用含x,y的式子表示)
(3)若内部粘贴角料的面积占长方体包装盒表面积的,求当,时,制作这样一个长方体共需要纸板多少平方厘米(含内部粘贴角料)?
【答案】(1)
(2)
(3)平方厘米
【解析】
【分析】本题考查了列代数式,代数式求值;
(1)根据长方体的体积公式,即可求解;
(2)根据长方体的表面积公式,即可求解;
(3)将,代入,即可求解.
【小问1详解】
解:由长方体包装盒的平面展开图,可知该长方体的长为厘米,宽为厘米,高为厘米,
则长方体包装盒的体积为立方厘米.
故答案为:;
【小问2详解】
长方体的表面积不含内部粘贴角料为平方厘米;
故答案为:;
【小问3详解】
长方体的长为厘米,宽为厘米,高为厘米,
长方体的表面积平方厘米,
又内部粘贴角料的面积占长方体表面纸板面积的,
制作这样一个长方体共需要纸板的面积平方厘米,
,,
制作这样一个长方体共需要纸为 平方厘米,
答:制作这样一个长方体共需要纸平方厘米.
22. 将直角三角板的直角顶点放在直线上,,射线平分.
(1)求的度数;
(2)试说明平分.
【答案】(1)
(2)见解析
【解析】
【分析】本题考查了角的计算,关键是掌握角平分线的性质.
(1)根据求解即可;
(2)先算出,再算出,可得与的关系,可得平分.
【小问1详解】
解:,
的度数为;
【小问2详解】
证明:,
射线平分,
,
,
平分.
23. 近年来,云南昆明不断完善全民健身公共服务体系,随着滇池绿道的建造,“15分钟健身圈”逐步形成,把“健身房”建在市民身边,让体育更好的融入生活.某工厂生产一批太空漫步器(如图).每套设备由3根立柱和4个脚踏板组装而成;工厂现共有40名工人,每人每天平均生产36根立柱或48个脚踏板,应如何分配工人才能使每天生产的立柱和脚踏板恰好配套?
【答案】20名工人生产立柱,20名工人生产脚踏板
【解析】
【分析】本题主要考查了一元一次方程的应用.设安排x人生产立柱,则安排人生产脚踏板,根据“每人每天平均生产36根立柱或48个脚踏板”,即可求解.
【详解】解:设安排x人生产立柱,则安排人生产脚踏板,由题意,得
,
解得,
,
答:安排20人生产立柱,20人生产脚踏板正好配套.
24. “距离”再探究.
概念理解】
“数形结合”是重要的数学思想.如:表示3与差的绝对值,也可以理解为3与在数轴上所对应的两个点之间的距离.进一步地,数轴上两个点A,B,所对应的数分别用a,b表示,那么A,B两点之间的距离表示为.利用此结论,回答以下问题:
(1)数轴上,点A,B表示的数分别是x,2,则A,B两点之间的距离可以表示为 .
A. B. C. D.
(2)【数学思考】数轴上,点C,D,E表示的数分别是2,4,10.点P是数轴上的动点,设点P表示的数是x.
(Ⅰ)的最小值为 ;
(Ⅱ)填写表格,并回答问题:
①处应填 .②处应填 .当 时,取最小值.
(3)【实际应用】在一条笔直的道路l上依次建有A,B,C,D四个停车场,其中B停车场靠近风景区,现准备在道路l上修建一个充电站P,请为充电站P选择一个合理的建造地点,并简要说明理由.
【答案】(1)D (2)(Ⅰ)2(Ⅱ)9;8;4
(3)点P在点B停车场最合适.理由:由奇中点偶中段可知,点P在线段BC上任何一点都可以使点P到四点距离之和最短,又由于点B停车场靠近风景区,所以点P在点B停车场最合适.
【解析】
【分析】本题考查数轴上两点的距离,化简绝对值,整式的加减,解答本题的关键是明确绝对值的定义,利用绝对值的知识和分类讨论的数学思想解答.
(1)由已知直接可得答案;
(2)(Ⅰ)是表示x的点P到表示2和4的点的距离之和,分类讨论根据绝对值的性质即可得答案;
(Ⅱ)将,分别代入即可求得空1和空2;分类讨论根据绝对值的性质即可得空3答案;
(3)利用(2)的结论即奇中点偶中段解决即可.
【小问1详解】
由A,B两点之间的距离表示为.
故选:D.
【小问2详解】
(Ⅰ)是表示x的点P到表示2和4的点的距离之和,
当时,原式;
当时,原式;
当时,原式;
∴当时,的最小为2;
故答案为:2.
(Ⅱ)当时,;
当时,;
表示数轴上有理数x所对应的点P到2、4和10所对应的点的距离和,
当时,原式;
当时,原式,
∴
当时,原式,
∴;
当时,原式,
∴;
∴当时,有最小值.
故答案为:9;8;4.
【小问3详解】
点P在点B停车场最合适.
理由:由奇中点偶中段可知,点P在线段上任何一点都可以使点P到四点距离之和最短,又由于点B停车场靠近风景区,所以点P在点B停车场最合适.x
…
3
4
5
6
…
…
①
②
9
10
…
云南省昆明市2023-2024学年七年级上学期期末数学试题(原卷+解析): 这是一份云南省昆明市2023-2024学年七年级上学期期末数学试题(原卷+解析),文件包含精品解析云南省昆明市2023-2024学年七年级上学期期末数学试题原卷版docx、精品解析云南省昆明市2023-2024学年七年级上学期期末数学试题解析版docx等2份试卷配套教学资源,其中试卷共19页, 欢迎下载使用。
云南省昆明市官渡区2023-2024学年九年级上学期期末数学试题(无答案): 这是一份云南省昆明市官渡区2023-2024学年九年级上学期期末数学试题(无答案),共7页。试卷主要包含了本卷为试题卷,下列事件是随机事件的是等内容,欢迎下载使用。
云南省昆明市官渡区昆一中学致学校2023-2024学年七年级上学期期中数学试题(原卷+解析): 这是一份云南省昆明市官渡区昆一中学致学校2023-2024学年七年级上学期期中数学试题(原卷+解析),文件包含精品解析云南省昆明市官渡区昆一中学致学校2023-2024学年七年级上学期期中数学试题原卷版docx、精品解析云南省昆明市官渡区昆一中学致学校2023-2024学年七年级上学期期中数学试题解析版docx等2份试卷配套教学资源,其中试卷共18页, 欢迎下载使用。












