



还剩9页未读,
继续阅读
所属成套资源:湘教版八年级数学下册【精品教学课件】
成套系列资料,整套一键下载
湘教版八年级数学下册 第1章 直角三角形 第1课时 直角三角形的性质和判定(课件)
展开
这是一份湘教版八年级数学下册 第1章 直角三角形 第1课时 直角三角形的性质和判定(课件),共17页。
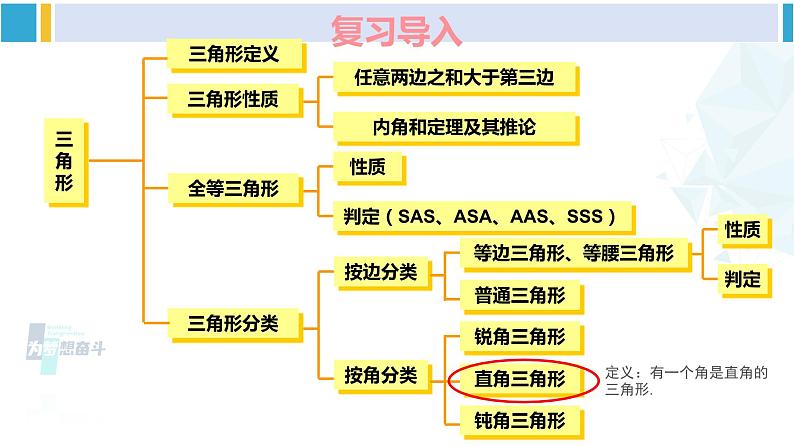
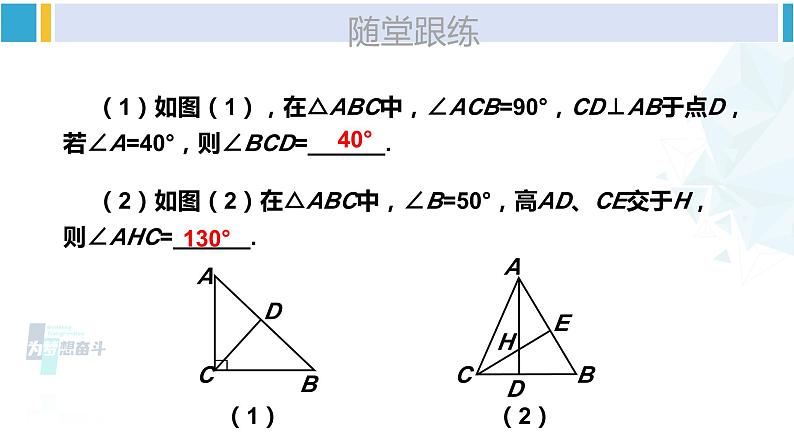
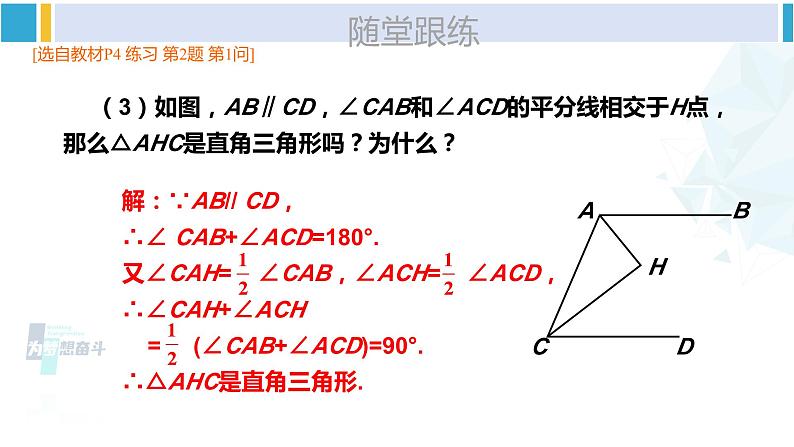
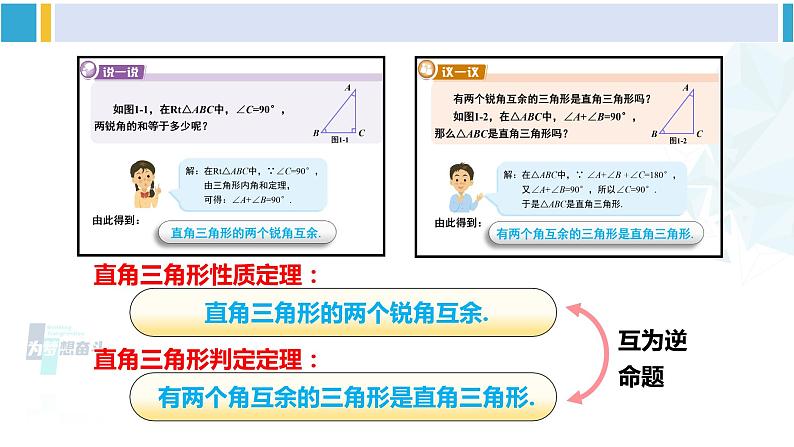
直角三角形的性质和判定湘教版·八年级数学下册①复习导入三角形定义三角形三角形性质定义:有一个角是直角的三角形.新课引入 如图1-1,在Rt△ABC中,∠C=90°,两锐角的和等于多少呢?解:在Rt△ABC中,∵∠C=90°, 由三角形内角和定理, 可得:∠A+∠B=90°.由此得到:Rt△两锐角关系动态演示随堂跟练 (1)如图(1),在△ABC中,∠ACB=90°,CD⊥AB于点D,若∠A=40°,则∠BCD=______. (2)如图(2)在△ABC中,∠B=50°,高AD、CE交于H,则∠AHC=______.40°130°(1) 有两个锐角互余的三角形是直角三角形吗?ABC图1-2 如图1-2,在△ABC中,∠A+∠B=90°,那么△ABC是直角三角形吗?解:在△ABC中,∵ ∠A+∠B +∠C=180°, 又∠A+∠B=90°,所以∠C=90°. 于是△ABC是直角三角形.由此得到:随堂跟练 (3)如图,AB∥CD,∠CAB和∠ACD的平分线相交于H点,那么△AHC是直角三角形吗?为什么?[选自教材P4 练习 第2题 第1问]解:∵AB// CD,∴∠ CAB+∠ACD=180°.又∠CAH= ∠CAB,∠ACH= ∠ACD, ∴∠CAH+∠ACH = (∠CAB+∠ACD)=90°.∴△AHC是直角三角形.直角三角形性质定理:直角三角形判定定理:互为逆命题 我测量后发现探究新知ABC图1-3 如图1-3,画一个Rt△ABC,并作出斜边AB上的中线CD,比较线段CD与线段AB之间的数量关系,你能得出什么结论?DAB= ;CD= ;度量AB、CD的长度:6cm3cmRt△中线与斜边关系动态演示探究新知由此得到:AB图1-4DC证明:如图1-4,过点D作DE⊥AC,交AC于点E;作DF⊥BC,交BC于点F.∵∠ACB= ∠AED=∠DFB = 90°,∴DE// BC,DF//AC.∴∠A=∠FDB,∠ADE=∠B.又D为AB的中点,即AD=DB,∴△AED≌△DFB (ASA).∴AE=DF, DE= BF.同理可证△CDE≌△DCF,从而DE=CF,CE= DF.∴AE=CE,BF= CF. 故DE, DF分别垂直平分边AC, BC. AD=CD=BD (为什么?) .由此得到:CD= AB例 1如图1-5,已知CD是△ABC的AB边上的中线,且CD= AB.求证:△ABC是直角三角形.证明:∵CD= AB=AD=BD,∴∠1=∠A,∠2=∠B.∵∠A+∠B+∠ACB=180°,∠ACB=∠1+∠2∴∠A+∠B +∠1+∠2 =180°.∴2( ∠A+∠B )=180°.∴∠A+∠B=90°.∴△ABC是直角三角形.(等边对等角)(三角形内角和的性质)(有两个角互余的三角形是直角三角形)由此得到:___________________________________________________________三角形一边上的中线等于这条边的一半的三角形是直角三角形.【教材P4】 三角形一边上的中线等于这条边的一半的三角形是直角三角形.直角三角形性质定理:直角三角形判定定理:互为逆命题巩固练习1.在Rt△ABC中,斜边上的中线CD=2.5cm,则斜边AB的长是多少?直角三角形性质定理:AB=5cm[选自教材P4 练习 第1题]巩固练习2.如图,AB∥CD,∠CAB和∠ACD的平分线相交于H点,E为AC的中点,EH=2.那么△AHC是直角三角形吗?为什么?若是,求出AC的长.解:△AHC是直角三角形,理由:∵AB∥CD,∴∠CAB+∠ACD=180°.∵AH,CH分别为∠CAB,∠ACD的平分线,∴∠CAH+∠ACH=90°.∴∠AHC=90°,即△AHC是直角三角形.∵E为AC的中点,∴AC=2EH=4.[选自教材P4 练习 第2题 第2问]巩固练习1.如图,CD是Rt△ABC的中线,∠ACB=90°, ∠CDA =120°,求∠B的度数.解:∵CD是Rt△ABC斜边AB上的中线,∴CD=DB=AD.∵∠CDA=120°,∴∠A=∠ACD=30°.在Rt△ABC中,∠A+∠B=90°,∴∠B=60°.[选自教材P7 习题1.1 A组 第1题]巩固练习2.如图,在△ABC中,已知∠B= ∠A= ∠C,AB=8 cm.(1)求证:△ABC为直角三角形;(2)求AB边上的中线长.(2)AB边上的中线长为4cm.[选自教材P7 习题1.1 A组 第2题]课堂小结直角三角形1.从课后习题中选取;2.完成练习册本课时的习题。课后作业
直角三角形的性质和判定湘教版·八年级数学下册①复习导入三角形定义三角形三角形性质定义:有一个角是直角的三角形.新课引入 如图1-1,在Rt△ABC中,∠C=90°,两锐角的和等于多少呢?解:在Rt△ABC中,∵∠C=90°, 由三角形内角和定理, 可得:∠A+∠B=90°.由此得到:Rt△两锐角关系动态演示随堂跟练 (1)如图(1),在△ABC中,∠ACB=90°,CD⊥AB于点D,若∠A=40°,则∠BCD=______. (2)如图(2)在△ABC中,∠B=50°,高AD、CE交于H,则∠AHC=______.40°130°(1) 有两个锐角互余的三角形是直角三角形吗?ABC图1-2 如图1-2,在△ABC中,∠A+∠B=90°,那么△ABC是直角三角形吗?解:在△ABC中,∵ ∠A+∠B +∠C=180°, 又∠A+∠B=90°,所以∠C=90°. 于是△ABC是直角三角形.由此得到:随堂跟练 (3)如图,AB∥CD,∠CAB和∠ACD的平分线相交于H点,那么△AHC是直角三角形吗?为什么?[选自教材P4 练习 第2题 第1问]解:∵AB// CD,∴∠ CAB+∠ACD=180°.又∠CAH= ∠CAB,∠ACH= ∠ACD, ∴∠CAH+∠ACH = (∠CAB+∠ACD)=90°.∴△AHC是直角三角形.直角三角形性质定理:直角三角形判定定理:互为逆命题 我测量后发现探究新知ABC图1-3 如图1-3,画一个Rt△ABC,并作出斜边AB上的中线CD,比较线段CD与线段AB之间的数量关系,你能得出什么结论?DAB= ;CD= ;度量AB、CD的长度:6cm3cmRt△中线与斜边关系动态演示探究新知由此得到:AB图1-4DC证明:如图1-4,过点D作DE⊥AC,交AC于点E;作DF⊥BC,交BC于点F.∵∠ACB= ∠AED=∠DFB = 90°,∴DE// BC,DF//AC.∴∠A=∠FDB,∠ADE=∠B.又D为AB的中点,即AD=DB,∴△AED≌△DFB (ASA).∴AE=DF, DE= BF.同理可证△CDE≌△DCF,从而DE=CF,CE= DF.∴AE=CE,BF= CF. 故DE, DF分别垂直平分边AC, BC. AD=CD=BD (为什么?) .由此得到:CD= AB例 1如图1-5,已知CD是△ABC的AB边上的中线,且CD= AB.求证:△ABC是直角三角形.证明:∵CD= AB=AD=BD,∴∠1=∠A,∠2=∠B.∵∠A+∠B+∠ACB=180°,∠ACB=∠1+∠2∴∠A+∠B +∠1+∠2 =180°.∴2( ∠A+∠B )=180°.∴∠A+∠B=90°.∴△ABC是直角三角形.(等边对等角)(三角形内角和的性质)(有两个角互余的三角形是直角三角形)由此得到:___________________________________________________________三角形一边上的中线等于这条边的一半的三角形是直角三角形.【教材P4】 三角形一边上的中线等于这条边的一半的三角形是直角三角形.直角三角形性质定理:直角三角形判定定理:互为逆命题巩固练习1.在Rt△ABC中,斜边上的中线CD=2.5cm,则斜边AB的长是多少?直角三角形性质定理:AB=5cm[选自教材P4 练习 第1题]巩固练习2.如图,AB∥CD,∠CAB和∠ACD的平分线相交于H点,E为AC的中点,EH=2.那么△AHC是直角三角形吗?为什么?若是,求出AC的长.解:△AHC是直角三角形,理由:∵AB∥CD,∴∠CAB+∠ACD=180°.∵AH,CH分别为∠CAB,∠ACD的平分线,∴∠CAH+∠ACH=90°.∴∠AHC=90°,即△AHC是直角三角形.∵E为AC的中点,∴AC=2EH=4.[选自教材P4 练习 第2题 第2问]巩固练习1.如图,CD是Rt△ABC的中线,∠ACB=90°, ∠CDA =120°,求∠B的度数.解:∵CD是Rt△ABC斜边AB上的中线,∴CD=DB=AD.∵∠CDA=120°,∴∠A=∠ACD=30°.在Rt△ABC中,∠A+∠B=90°,∴∠B=60°.[选自教材P7 习题1.1 A组 第1题]巩固练习2.如图,在△ABC中,已知∠B= ∠A= ∠C,AB=8 cm.(1)求证:△ABC为直角三角形;(2)求AB边上的中线长.(2)AB边上的中线长为4cm.[选自教材P7 习题1.1 A组 第2题]课堂小结直角三角形1.从课后习题中选取;2.完成练习册本课时的习题。课后作业
相关资料
更多









