
所属成套资源:【学霸计划】2024年中考数学大复习-知识点记诵版
第10讲 三角形与全等三角形(知识点梳理)(记诵版)-【学霸计划】2024年中考数学大复习
展开
这是一份第10讲 三角形与全等三角形(知识点梳理)(记诵版)-【学霸计划】2024年中考数学大复习,共7页。
考点01 与三角形有关的线段
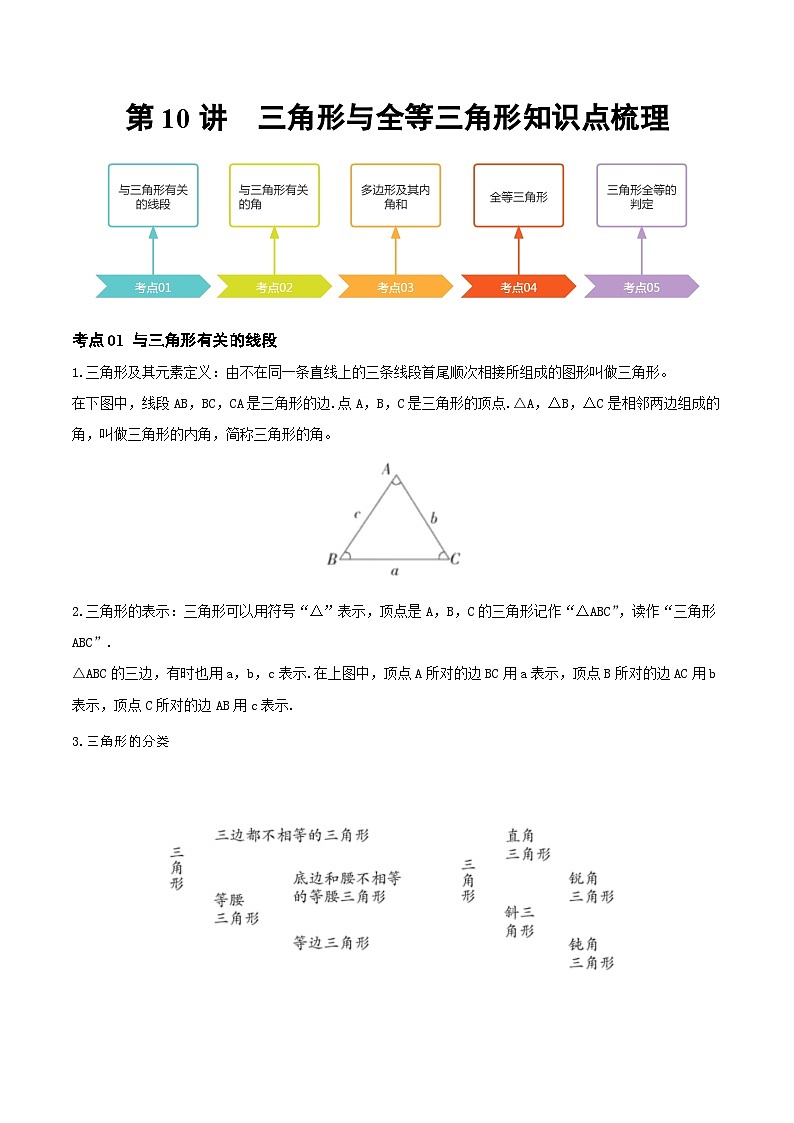
1.三角形及其元素定义:由不在同一条直线上的三条线段首尾顺次相接所组成的图形叫做三角形。
在下图中,线段AB,BC,CA是三角形的边.点A,B,C是三角形的顶点.△A,△B,△C是相邻两边组成的角,叫做三角形的内角,简称三角形的角。
2.三角形的表示:三角形可以用符号“△”表示,顶点是A,B,C的三角形记作“△ABC”,读作“三角形ABC”.
△ABC的三边,有时也用a,b,c表示.在上图中,顶点A所对的边BC用a表示,顶点B所对的边AC用b表示,顶点C所对的边AB用c表示.
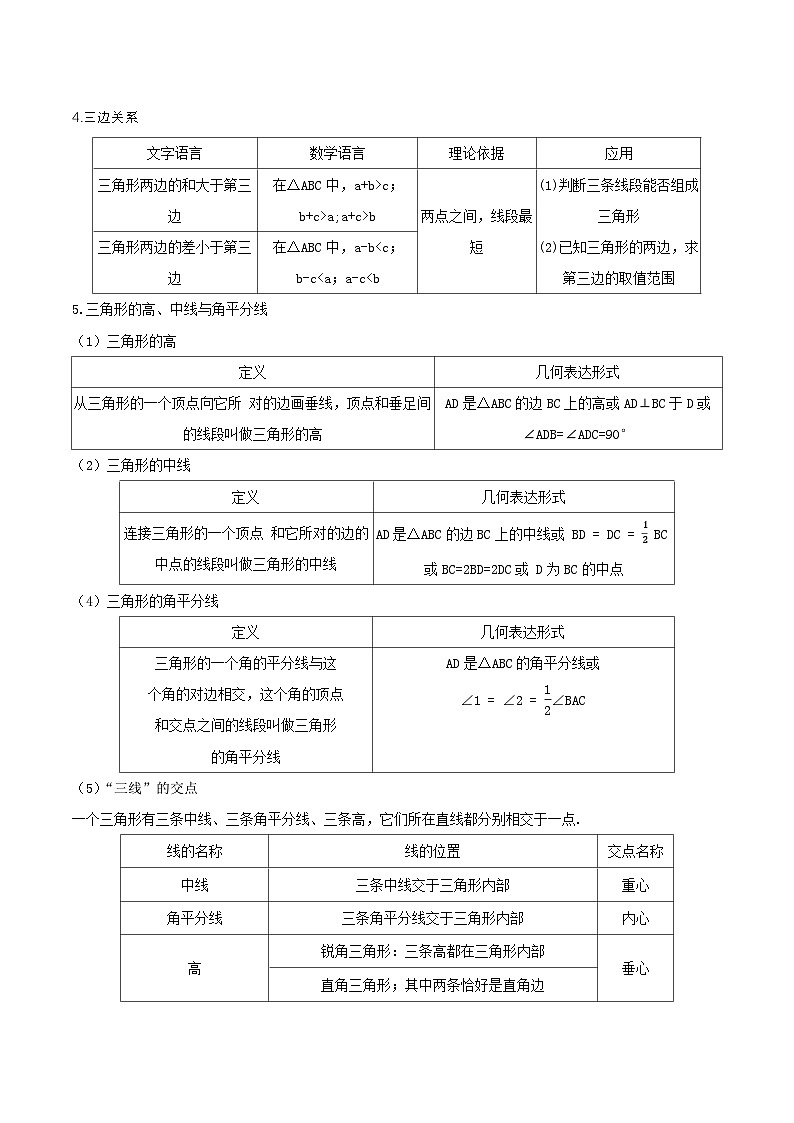
3.三角形的分类
4.三边关系
5.三角形的高、中线与角平分线
(1)三角形的高
(2)三角形的中线
(4)三角形的角平分线
(5)“三线”的交点
一个三角形有三条中线、三条角平分线、三条高,它们所在直线都分别相交于一点.
注意:三角形的高、中线、角平分线都是线段。
6.三角形的稳定性
三角形具有稳定性,而四边形没有稳定性.
三角形的稳定性有广泛的应用:桥梁、起重机、人字型屋顶等.
考点02 与三角形有关的角
1.三角形的内角
(1)三角形内角和定理:三角形三个内角的和等于180°.
(2)证明方法
剪拼成平角、通过作平行线构造平角,构造两平行线下的同旁内角。
2.直角三角形的性质与判定
(1)性质:直角三角形的两个锐角互余。
直角三角形可以用符号“Rt△”表示,直角三角形ABC可以写成Rt△ABC。
(2)判定:有两个角互余的三角形是直角三角形。
如下图,在△ABC中,如果∠A+∠B=90°,那么△ABC是直角三角形。
3.三角形的外角
(1)定义:三角形的一边与另一边的延长线组成的角,叫做三角形的外角.如图,∠ABD是△ABC的一个外角。
(2)性质:三角形的外角等于与它不相邻的两个内角的和;三角形的外角大于与它不相邻的任何一个内角;三角形的外角和为360°。
考点03 多边形及其内角和
1.多边形
(1)定义:在平面内,由一些线段首尾顺次相接组成的封闭图形叫做多边形。
(2)多边形的内角;多边形相邻两边组成的角叫做多边形的内角。
(3)多边形的外角:多边形的边与它的邻边的延长线组成的角叫做多边形的外角。
如图,∠2是五边形ABCDE的一个外角。
(4)多边形的对角线:连接多边形不相邻的两个顶点的线段,叫做多边形的对角线.
(5)凸多边形:画出多边形的任何一条边所在直线,如果整个多边形都在这条直线的同一侧,那么这个多边形就是凸多边形.
(6)正多边形:各个角都相等,各条边都相等的多边形叫做正多边形.一个n边形从一个顶点出发有(n-3)条对角线,所有对角线的数量是 nn−32条
2.多边形的内角和、外角和
(1)多边形内角和公式:n边形内角和等于(n-2)×180°,
(2)定理:多边形的外角和等于360°.多边形的外角和恒等于360°,与多边形的边数无关.
(3)正n边形的每个内角等于 n−2n⋅180°,每个外角等于360°。
考点04 全等三角形
1.全等形:能够完全重合的两个图形叫做全等形.
2.全等三角形的相关概念及表示方法
(1)相关概念
能够完全重合的两个三角形叫做全等三角形。
把两个全等的三角形重合到一起,重合的顶点叫做对应顶点,重合的边叫做对应边,重合的角叫做对应角。
(2)表示方法
全等的符号:“≌”,读作“全等于”。
△ABC与△DEF全等,记作;△ABC≌△DEF,读作:“三角形ABC全等于三角形DEF".
记两个三角形全等时,通常把表示对应顶点的字母写在对应的位置上.△ABC和△DBC全等,点A和点D,点B和点B,点C和点C是对应顶点,记作△ABC≌△DBC。
3.全等三角形的性质:全等三角形的对应边相等,全等三角形的对应角相等。
4.确定全等三角形对应边、对应角的方法
(1)若有公共边,则公共边一定是对应边。
(2)一对最长的边一定是对应边,一对最短的边也一定是对应边。
(3)若有公共角,则公共角一定是对应角。
(4)若有对顶角,则对顶角一定是对应角。
(5)一对最大的角一定是对应角,一对最小的角也一定是对应角。
(6)两边是对应的,则它们所对的角也一定是对应的;反过来,两个角是对应的,则它们所对的边也是对应的。
(7)两条对应边所夹的角是对应角,两对对应角所夹的边是对应边。
(8)两个三角形全等用“>”表示,找对应边、对应角一般可以从其书写的顺序和位置上来找。
考点05 三角形全等的判定
1.三角形全等的判定方法
(1)SSS(边边边):三边分别相等的两个三角形全等。
(2)SAS(边角边):两边和它们的夹角分别相等的两个三角形全等。
(3)ASA(角边角):两角和它们的夹边分别相等的两个三角形全等。
(4)AAS(角角边):两角和其中一个角的对边分别相等的两个三角形全等。
(5)HL(斜边、直角边):斜边和一条直角边分别相等的两个直角三角形全等。
2.合理选择全等三角形的判定方法
(1)已知两边:①找夹角→SAS;②找第三边→SSS;③找直角→HL。
(2)已知两角:①找夹边→ASA;②找其中一个已知角的对边→AAS。
边为角的对边→找任一角→AAS
(3)已知一边一角
①边为角的对边:找任意一角→AAS;
②边为角的邻边:找夹角的另一边→SAS;找夹边的另一角→ASA;找边的对角→AAS。
4.角的平分线的性质:角的平分线上的点到角的两边的距离相等.如图,因为点P在△AOB的平分线上,PC上OA于点C,PD⊥OB于点D,所以PC=PD。
5.角的平分线的判定
角的内部到角的两边的距离相等的点在角的平分线上.如上图,因为PC⊥0A,PD⊥OB,PC=PD,所以点P在∠AOB的平分线上。
文字语言
数学语言
理论依据
应用
三角形两边的和大于第三边
在△ABC中,a+b>c;
b+c>a;a+c>b
两点之间,线段最短
(1)判断三条线段能否组成三角形
(2)已知三角形的两边,求第三边的取值范围
三角形两边的差小于第三边
在△ABC中,a-b
相关学案
这是一份备战中考初中数学导练学案50讲—第19讲全等三角形(讲练版),共26页。学案主要包含了疑难点拨,问题发现,类比探究,拓展应用等内容,欢迎下载使用。
这是一份(通用版)中考数学总复习知识点梳理第27讲《概率》学案,共1页。
这是一份(通用版)中考数学总复习知识点梳理第26讲《统计》学案,共2页。









