
黑龙江省哈尔滨市萧红中学校2023-2024学年九年级下学期开学考试数学试题
展开提示:请将答案作答在题卡上,否则无效。
一、选择题(每小题3分,共30分)
1.下列各数中最小的数是…………( )
A.−1B.0C.1D.3
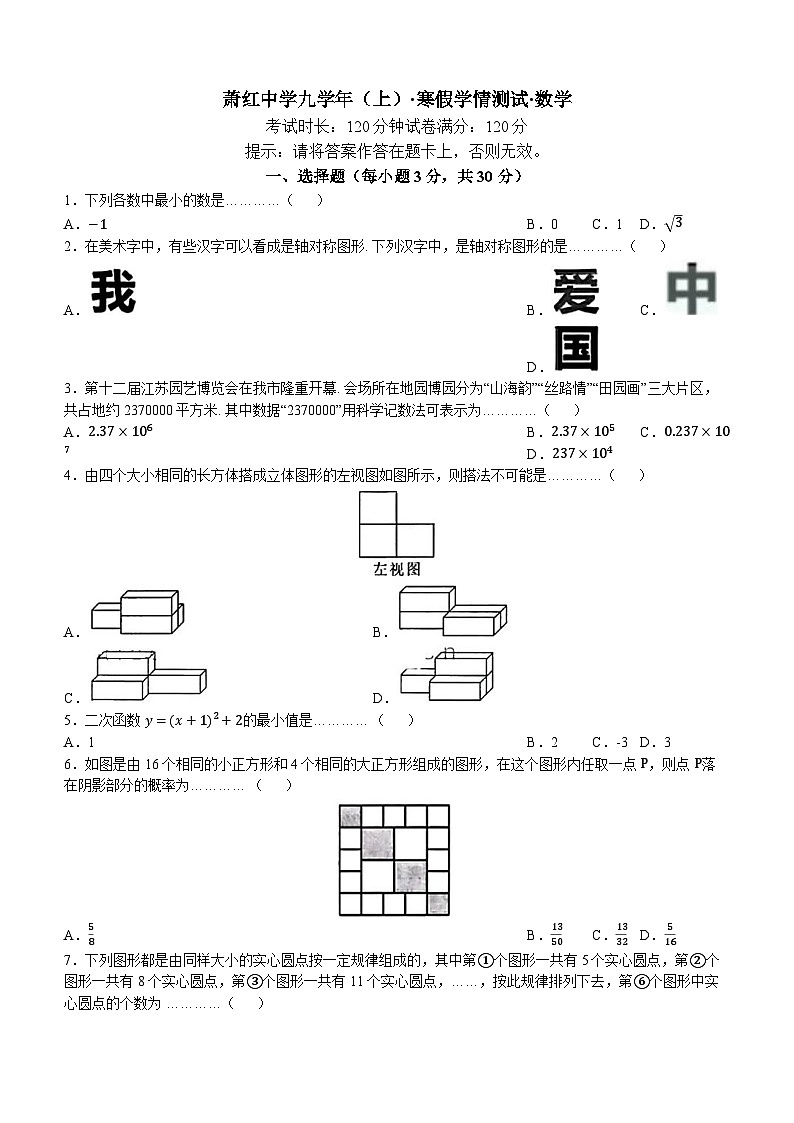
2.在美术字中,有些汉字可以看成是轴对称图形. 下列汉字中,是轴对称图形的是…………( )
A.B.C.D.
3.第十二届江苏园艺博览会在我市隆重开幕. 会场所在地园博园分为“山海韵”“丝路情”“田园画”三大片区,共占地约2370000平方米. 其中数据“2370000”用科学记数法可表示为…………( )
A.2.37×106B.2.37×105C.0.237×107D.237×104
4.由四个大小相同的长方体搭成立体图形的左视图如图所示,则搭法不可能是…………( )
A.B.
C.D.
5.二次函数 y=x+12+2的最小值是………… ( )
A.1B.2C.-3D.3
6.如图是由16个相同的小正方形和4个相同的大正方形组成的图形,在这个图形内任取一点 P,则点 P落在阴影部分的概率为………… ( )
A.58B.1350C.1332D.516
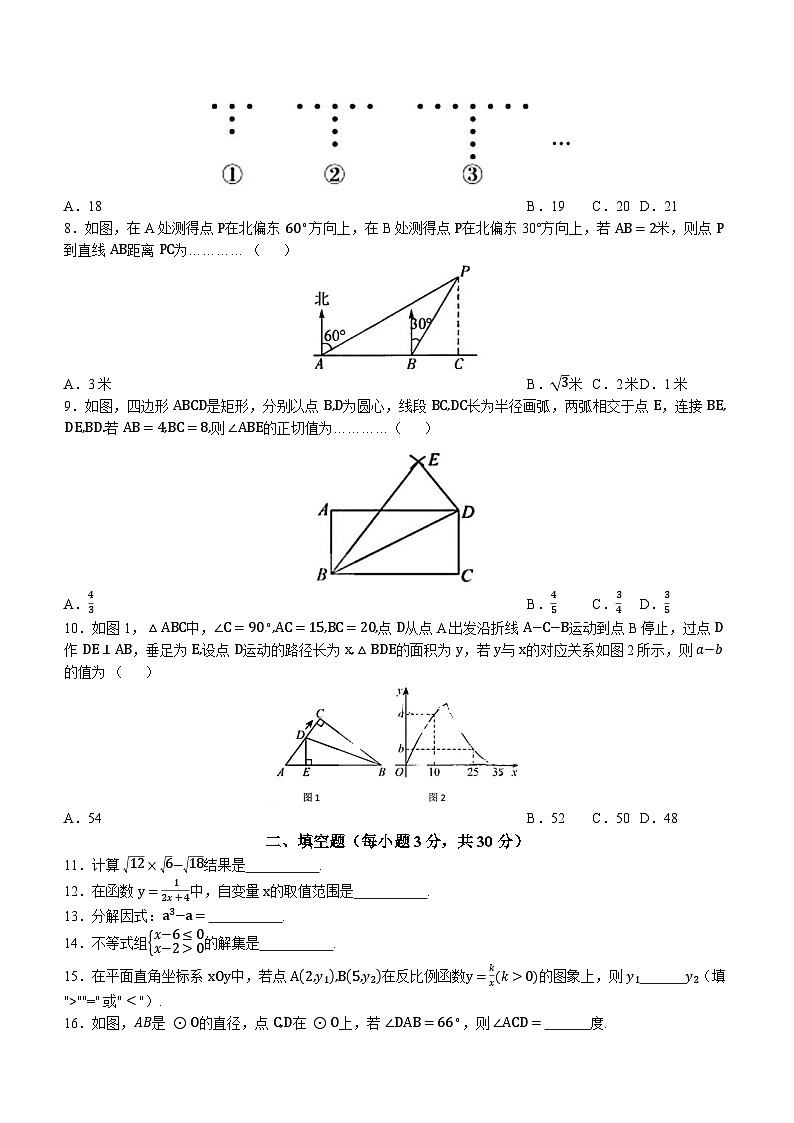
7.下列图形都是由同样大小的实心圆点按一定规律组成的,其中第①个图形一共有5个实心圆点,第②个图形一共有8个实心圆点,第③个图形一共有11个实心圆点,……,按此规律排列下去,第⑥个图形中实心圆点的个数为 …………( )
A.18B.19C.20D.21
8.如图,在 A处测得点 P在北偏东 60∘方向上,在 B处测得点 P在北偏东30°方向上,若 AB=2米,则点 P到直线 AB距离 PC为………… ( )
A.3米B.3米C.2米D.1米
9.如图,四边形 ABCD是矩形,分别以点 B,D为圆心,线段 BC,DC长为半径画弧,两弧相交于点 E,连接 BE,DE,BD.若 AB=4,BC=8,则 ∠ABE的正切值为…………( )
A.43B.45C.34D.35
10.如图1,△ABC中,∠C=90∘,AC=15,BC=20,点 D从点 A出发沿折线 A−C−B运动到点 B停止,过点 D作 DE⊥AB,垂足为 E,设点 D运动的路径长为 x,△BDE的面积为 y,若 y与 x的对应关系如图2所示,则 a−b的值为 ( )
A.54B.52C.50D.48
二、填空题(每小题3分,共30分)
11.计算 12×6−18结果是 .
12.在函数 y=12x+4中,自变量 x的取值范围是 .
13.分解因式:a3−a= .
14.不等式组x−6≤0x−2>0的解集是 .
15.在平面直角坐标系 xOy中,若点 A2,y1,B5,y2在反比例函数y=kxk>0的图象上,则 y1 y2(填 ">""="或"<").
16.如图,AB是 ⊙O的直径,点 C,D在 ⊙O上,若 ∠DAB=66∘,则 ∠ACD= 度.
17.一个扇形的面积为 6π,其弧长为 2π,则它的圆心角度数为 .
18.如图,在 △ABC中,D、E、F分别在 AB、AC、BC上,DE//BC,EF//AB,AD=9,EF=6,CF=5,,则 BF的长为 .
19.矩形 ABCD中, M为对角线 BD的中点,点 N在边 AD上,且 AN=AB=1. 当以点 D,M,N为顶点的三角形是直角三角形时,AD的长为 .
20.如图,四边形 ABCD,AD=AB=BC,∠ACD=30∘,tan∠BAC=233,CD=3,则 AC= .
三、解答题(其中 21~24题各7分,25、26题各10分,27题12分,共60分)
21.(7分)先化简,再求代数式 1x2−2x−1x2−4x+4÷2x2−2x的值,其中 x=2tan45∘−cs30∘.
22.(7分)图1、图2均是 4×4的正方形网格,每个小正方形的顶点称为格点小正方形的边长为1,线段 AB的端点 A,B均在格点上,在给定的网格中按要求画图,所画图形的顶点均在格点上.
(1)在图1中,以 AB为底边画一个等腰 △ABC;
(2)在图2中,以 AB为一边画一个面积为7的 ▱ ABDE.
(3)直接写出线段 BE的长.
23.(8分)萧红中学为了了解学生“最喜爱的省运会项目"的情况,随机抽取了部分学生进行问卷调查,规定每人从“篮球”、羽毛球”、自行车”、游泳"和“其他”五个选项中必须选择且只能选择一个,并将调查结果绘制成如下两幅不完整的统计图表.
最喜爱的省运会项目的人数调查统计表
根据以上信息,请回答下列问题:
(1)这次调查的样本容量是 ,a+b= ;
(2)扇形统计图中“自行车”对应的扇形的圆心角为 度;
(3)若该校有1200名学生,估计该校最喜爱的省运会项目是篮球的学生人数.
24.(8分)如图,△ABC中,∠ABC=90∘,CD=AB,过点 D作 DE⊥BC,DE=BC.
(1)求证 :△ACE是等腰直角三角形;
(2)延长 DE至 F,使得 EF=CD,连接BF并与 CE的延长线相交于点 G,求 ∠BGC的度数.
25.(10分)服装店去年10月以每套 1200元的进价购进一批羽绒服,当月以标价销售,销售额28000元,进入11月份搞促销活动,每件让利 100元,这样销售额比10月份增加了11000元,销售量是 10月份的1.5倍.
(1)求每件羽绒服的标价是多少元;
(2)进入12月份,服装店决定把剩余羽绒服九折甩货,全部卖掉,这批羽绒服总获利不少于9940元,问这批羽绒服至少购进多少件?
26.(10分)在⊙O中,AB为直径,CD为弦,弧 AC=弧 BE.
(1)如图1,求证:AB//CD;
(2)如图2,过点 D作 ⊙O的切线,交 AB延长线于点 E,交 AC延长线于点 F,求证:2∠A=∠E+90∘;
(3)如图3,在(2)的条件下,P为 AB上一点,∠FDP=∠CPA+∠DPA,AO=4,CP=6,求 DP的长.
27.(10分)在平面直角坐标系中,点 0为坐标原点,抛物线 y=ax2+x+6交 x轴负半轴于 A,交正半轴于 B,交 y轴于 C,OB=OC.
(1)求抛物线的解析式;
(2)如图1,点 P是第三象限抛物线上一点,连接 BP交 y轴于点 D,设点 P横坐标为 t,线段 CD长为 d,求 d与 t的函数关系;
(3)如图2,在 (2)的条件下,过点 C作 BP的垂线,交 x轴于点 F,垂足为点 G,E为 CF上一点,连接 BE,若 BE=BD,∠BEG=2∠PBA,求点 P坐标.
【参考答案】
萧红中学九学年(上)·寒假学情测试·数学
一、选择题(每小题3分,共30分)
1.A 2.C 3.A 4.A 5.B 6.B 7.C 8.B 9.C 10.B
二、填空题(每小题3分,共30分)
11.32
12.x≠−2
13.aa+1a−1
14.2
16.24∘
17.60°
18.152
19.2或 11+2
20.37
三、解答题(其中 21~24题各7分,25、26题各10分,27题12分,共60分)
21.
解:原式=[1xx−2−1x−22]⋅xx−22⋯⋯⋅2分
=x−2−xxx−22⋅xx−22⋯⋯⋅1分 =12−x,⋯⋯1分
∵x=2tan45∘−cs30∘=2×1−32=2−3,⋯⋯⋅2分
∴原式=12−2−3=13=33⋅⋯⋯⋅1分
22.(1)
解:如图所示,
(2)
如图所示,
(3) BE=17
23.(1) 50; 11
(2) 72
(3) 解:该校最喜爱的省运会项目是篮球的学生人数为 1200×2050=480(人)
24.(1)
证明 DE⊥BC,
∠EDC=90∘=∠CBA,
∠DCE+∠DEC=90∘,
在△ABC和△CDE中,
AB=CD∠ABC=∠CDEBC=DE,
∴△ABC≅△CDESAS,
∴∠ACB=∠DEC,AC=CE,
∴∠ACB+∠DCE=∠ACE=90∘,
∴△ACE是等腰直角三角形;
(2)
∵AB⊥BC,DE⊥BC,
∴AB∥DF,
∵△ABC≅△CDE(已证),
∴AB=CD,
∵EF=CD,
∴AB=EF,
四边形 AEFB平行四边形,
∴BF∥AE,
∴∠BGC=∠AEC,
∵△ACE等腰直角三角形,
∴∠BGC=∠AEC=45.
25.(1)
设每件羽绒服的标价为x元,则 10月份售出 12000x件,
根据题意得:28000+11000x−100=28000x×1.5,
解得:x=1400,
经检验 x=1400是原方程的解,
答:每件羽绒服的标价为1400元.
(2)
设这批羽绒服购进a件,
10月份售出 128000÷1400=20(件),11月份售出 20×1.5=3(件)
根据题意得:28000+11000+28000+1400×0.9a−20−30−1200a≥9940解得 :a≥99,
所以a至少是99,
答:这批羽绒服至少购进99件.
26.(1) 连 AD,得等角,内错角得平行…………2分
(2) 连 CO,DO,导角可证…………3分
(3)
延长 DO交⊙O于点 G,延长 GP交 EF于H,
证等圆心角,…………1分;证全等,…………1分;导角证 DH=HP,…………1分
勾 △DGH求 DH=73,得 tan∠GHD=247,…………1分
解 △DHP求 DP=145…………分
27.(1)
点 C0,6,点 B(6,0)…………1分
待定系数法求解析式为 y=−13x2+x+6…………1分
(2) d=−2t…………3分
(3)
核心:立倒全等+还原错位角分线
最喜爱的项目
人数
篮球
20
羽毛球
9
自行车
10
游泳
a
其他
b
合计
证全等,得 OF=OD…………1分
构对称,2倍角变等角…………1分
构全等,得BG=KF’…………1分
平八全等导边得OB=3OF…………1分
D(0,-2)
法1:求直线BP解析式与抛 物线相交,求交点P坐标
法2:求CD长,用2问结论 定P横坐标,在代入解析式求 纵 结论:P4,−103…………1分
黑龙江省哈尔滨市重点学校2023-2024学年九年级下学期开学考试数学试题(含答案): 这是一份黑龙江省哈尔滨市重点学校2023-2024学年九年级下学期开学考试数学试题(含答案),共10页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
黑龙江省哈尔滨市萧红中学2023-2024学年九年级上学期月考数学试题(无答案): 这是一份黑龙江省哈尔滨市萧红中学2023-2024学年九年级上学期月考数学试题(无答案),共5页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
黑龙江省哈尔滨市南岗区萧红中学2023-2024学年九年级上学期开学考试数学(五四制)试题: 这是一份黑龙江省哈尔滨市南岗区萧红中学2023-2024学年九年级上学期开学考试数学(五四制)试题,共8页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。












