苏科版八年级下册11.1 反比例函数达标测试

这是一份苏科版八年级下册11.1 反比例函数达标测试，文件包含第11章反比例函数章末检测卷培优分阶练原卷版docx、第11章反比例函数章末检测卷培优分阶练解析版docx等2份试卷配套教学资源，其中试卷共34页， 欢迎下载使用。

一、选择题（本大题共10小题，每小题3分，共30分）在每小题所给出的四个选项中，只有一项是符合题目要求的．
1．（2023秋·广东江门·九年级统考期末）下列函数中，反比例函数是（ ）
A．B．C．D．
2．（2023·重庆·二模）已知某用电器的输出功率为、电阻为，通过的电流为，当为定值时，下面说法正确的是（ ）
A．是的正比例函数 B．是的正比例函数 C．是的反比例函数 D．是的反比例函数
3．（2023秋·河南开封·九年级统考期末）已知点在反比例函数的图象上，则点P关于原点对称的点的坐标是（ ）
A．B．C．D．
4．（2022·哈尔滨九年级期中）双曲线y＝的图象分布在第二、四象限，则k的取值范围是（ ）
A．k≤3B．k＜3C．k＞3D．k≥3
5．（2022·湖南湘潭·模拟预测）如图，过反比例函数的图象上任意两点A、B分别作x轴的垂线，垂足分别为C、D，连接、，设和的面积分别是、，比较它们的大小，可得（ ）
A．B．C．D．大小关系不能确定
6．（2023·湖北襄阳·校考一模）对于反比例函数，下列说法不正确的是（ ）
A．图象关于对称B．当时，y随x的增大而增大
C．图象位于第一、三象限D．当时，则
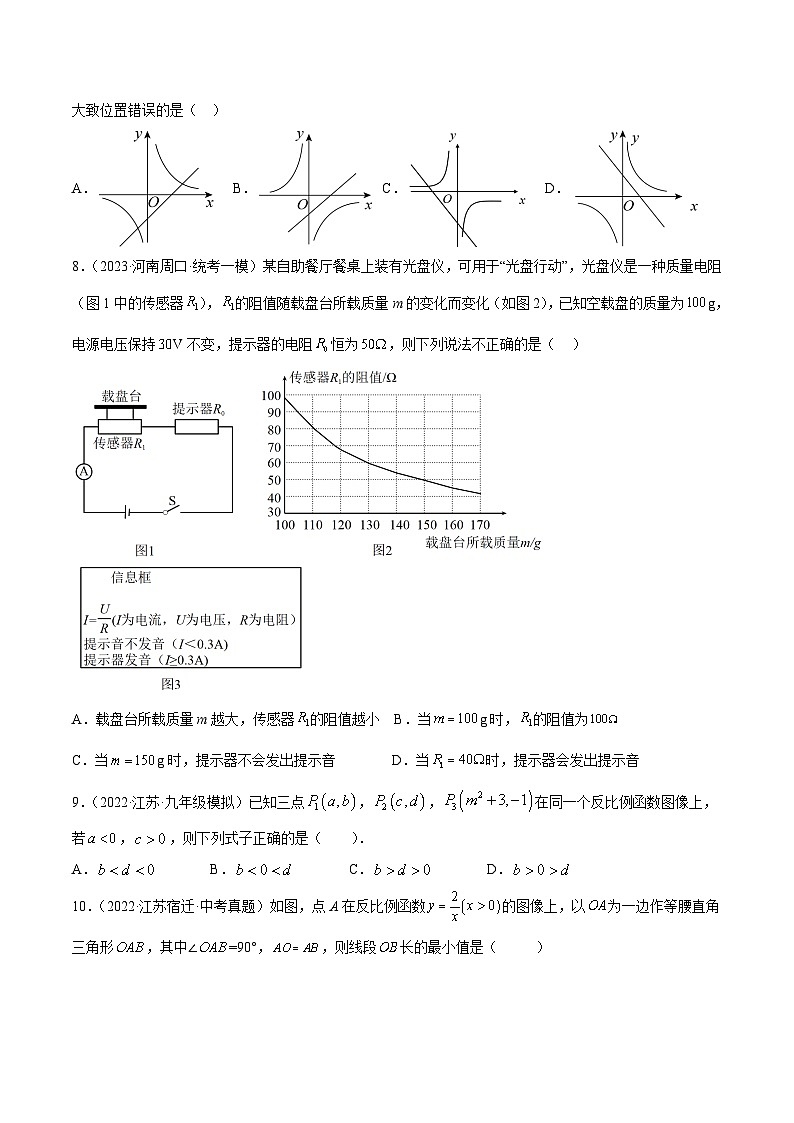
8．（2023秋·山东滨州·九年级统考期末）如图，同一坐标系中，直线与双曲线大致位置错误的是（ ）
A． B． C． D．
8．（2023·河南周口·统考一模）某自助餐厅餐桌上装有光盘仪，可用于“光盘行动”，光盘仪是一种质量电阻（图1中的传感器），的阻值随载盘台所载质量m的变化而变化（如图2），已知空载盘的质量为g，电源电压保持V不变，提示器的电阻恒为，则下列说法不正确的是（ ）
A．载盘台所载质量m越大，传感器的阻值越小 B．当g时，的阻值为
C．当g时，提示器不会发出提示音 D．当时，提示器会发出提示音
9．（2022·江苏·九年级模拟）已知三点，，在同一个反比例函数图像上，若，，则下列式子正确的是（ ）．
A．B．C．D．
10．（2022·江苏宿迁·中考真题）如图，点A在反比例函数的图像上，以为一边作等腰直角三角形，其中∠=90°，，则线段长的最小值是（ ）
A．1B．C．D．4
二、填空题（本大题共8小题，每小题3分，共24分．不需写出解答过程，请把答案直接填写在横线上）
11．（2023秋·天津南开·九年级统考期末）已知y与成反比例，并且当x＝3时，y＝4．则y与x之间的函数解析式为______．
12．（2021·江苏淮安区·八年级期末）已知反比例函数（k是常数， 1）的图象分布在二、四象限，那么k的取值范围是___________．
13．（2022·陕西西安市·九年级二模）若直线y＝kx与双曲线y＝﹣交于A(x1，y1)、B(x2，y2)两点，则3x1y2+2x2y1的值为_____．
14．（2022春·浙江·八年级阶段练习）根据某商场对一款运动鞋五天中的售价与销量关系的调查显示，售价是销量的反比例函数（统计数据见下表）．已知该运动鞋的进价为元/双，要使该款运动鞋每天的销售利润达到元，则其售价应定为__________元．
15．（2023·江苏南京·校联考一模）若函数（k为常数，且）过点，当时，y的取值范围是__________．
16．（2022·江苏徐州市·八年级期末）如图，点A在函数y＝的图像上，过A作AB∥x轴，AB与y＝的图像交于点B，点C、D在x轴上，若AB＝DC，则四边形ABCD的面积为 ___．
17．（2022·浙江八年级月考）如图，等腰直角三角形的一条直角边在轴上，点是边上的一个动点，过点的反比例函数的图象交斜边于点，（1）当为中点时，_________（2）若为的三等分点，当的面积为时，的值为________．
18．（2022·江苏靖江市·八年级期中）如图，在平面直角坐标系中，正方形的顶点O与原点重合，顶点A，C分别在x轴，y轴上，反比例函数的图像与正方形的两边，分别交于点M，N，连接，，，若，，则k的值为________．
三、解答题（本大题共8小题，共66分．请在答题卡指定区域内作答，解答时应写出文字说明、证明过程或演算步骤）
19．（2022·浙江余姚市·八年级期末）已知反比例函数y=（k≠0）的图象经过点A（2，-3）．
（1）求函数表达式；（2）当x=-4时，求函数y的值；（3）当x≤1且x≠0时，直接写出y的取值范围．
20．（2022·辽宁抚顺市·九年级三模）教师办公室有一台可以自动加热的饮水机，该饮水机的工作程序是：放满水后，接通电源，则自动开始加热．每分钟水温上升10℃，待加热到100℃时，饮水机自动停止加热，水温开始下降．在水温开始下降的过程中，水温y（℃）和通电时间x（）成反比例关系．直至水温降至室温，饮水机再次自动加热，重复上述过程．设某天水温和室温均为20℃，接通电源后，水温y（℃）和通电时间x（）之间的关系如图所示，回答下列问题：（1）分别求出当和时，y和x之间的函数关系式；（2）求出图中a的值；（3）李老师这天7：30将饮水机电源打开，若他想在8：10上课前喝到不低于40℃的开水，则他需要在通电多长时间内接水？
21．（2022安徽九年级月考）如图，直线与双曲线相交于A，B两点，与y轴交于点C，轴，垂足为D，已知．（1）求此双曲线的函数表达式；（2）求点A，B的坐标；（3）直接写出不等式的解集
22．（2022·佛山市九年级月考）如图，一次函数的图象与反比例函数的图象相交于、两点，其中点的坐标为，点的纵坐标为．（1）求这两个函数的表达式；（2）点为反比例函数图象上的一点，且点在点的上方，当时，求点的坐标．
23．（2022·沙坪坝区·九年级月考）小明根据学习函数的经验，对函数的图象和性质进行了探究，下面是小明的探究过程，请补充完整，并解决相关问题：（1）如表是与的几对对应值：
其中 ， ；（2）函数图象与轴的交点坐标是 ；（3）在平面直角坐标系中，画出函数的图象；
（4）结合图象，写出函数的一条性质： ；（5）观察函数图象，将直线向上平移个单位，使得平移后的直线与该函数图象恰好有两个交点，则的值是 ．
24．（2022·安徽淮北·九年级月考）如图，在平面直角坐标系中，一次函数的图象与反比例函数的图象交于点和点．（1）求一次函数与反比例函数的表达式；（2）直线与轴交于点，与轴交于点．①过点作轴交反比例函数的图象于点，连接，试判断的形状，并说明理由；②设是轴上一点，当时，求点的坐标．
25．（2022·重庆九年级期中）如图，已知直线与双曲线交于两点，且点坐标为（）. （1）求双曲线解析式及点坐标；（2）将直线向下平移一个单位得直线，是轴上的一个动点，是上的一个动点，求的最小值；（3）若点为轴上的一个动点，为平面内一个动点，当以、、为顶点的四边形是矩形时，直接写出点坐标．

26．（2022·江苏丹阳·八年级期末）我国著名数学家华罗庚先生曾说：“数缺形时少直观，形缺数时难入微，数形结合百般好，隔裂分家万事休”．数形结合是解决数学问题的重要思想方法．
阅读下列材料，回答问题：对任意的实数a、b而言，a2﹣2ab+b2＝（a﹣b）2≥0，即a2+b2≥2ab．
易知当a＝b时，（a﹣b）2＝0，即：a2﹣2ab+b2＝0，所以a2+b2＝2ab．
若a≠b，则（a﹣b）2＞0，所以a2+b2＞2ab．
[类比论证]对于任意正实数a、b，∵≥0，∴a+b 2ab（填“＜”、“＞”、“≤”或“≥”）
[几何验证]如图（1），在△ABC中，∠ACB＝90°，CD⊥AB于点D，CE为△ABC的中线，若AD＝a，BD=b，试根据图形证明：a+b≥2．
[结论应用]若a＞0，则当a＝ 时，代数式a+有最小值为 ．
[问题解决]（1）某汽车零件生产公司为提高工作效率，购进了一批自动化生产设备，已知每台设备每天的运营成本包含以下三个部分：一是固定费用，共3600元；二是材料损耗费，每个零件损耗约为5元（元），三是设备折旧费（元），它与生产的零件个数x的函数关系式为0.0001x2，设该设备每天生产汽车零件x个．当x为多少时，该设备每生产一个零件的运营成本最低？最低是多少元？（2）如图（2），在平面直角坐标系中，直线y＝﹣4与坐标轴分别交于点A、B，点M为反比例函数y＝（x＞0）上的任意一点，过点M作MC⊥x轴于点C, MD⊥y轴于点D．则四边形ABCD面积的最小值为 ．
售价x（元/双）
200
250
300
400
销售量y（双）
30
24
20
15
0
1
2
3
4
5
3