九年级下册第三章 圆4 圆周角和圆心角的关系示范课ppt课件

这是一份九年级下册第三章 圆4 圆周角和圆心角的关系示范课ppt课件，共28页。PPT课件主要包含了逐点学练，课堂小结，作业提升，学习目标，本节要点，学习流程，知识点，感悟新知，圆周角，圆周角定理的推论等内容，欢迎下载使用。
圆周角圆周角定理的推论圆内接四边形
1. 圆周角的定义 顶点在圆上，两边分别与圆还有另一个交点，像这样的角，叫做圆周角.特征 圆周角必须满足两个条件：①顶点在圆上；②两边都和圆相交.
特别提醒圆心角与圆周角的区别与联系：
2. 圆周角定理 圆周角的度数等于它所对弧上的圆心角度数的一半.如图3-4-1，∠ ACB= ∠ AOB.特别警示：定理中的圆周角与圆心角是通过它们所对的同一条弧联系在一起的，故不能把同一条弧这个前提省略.
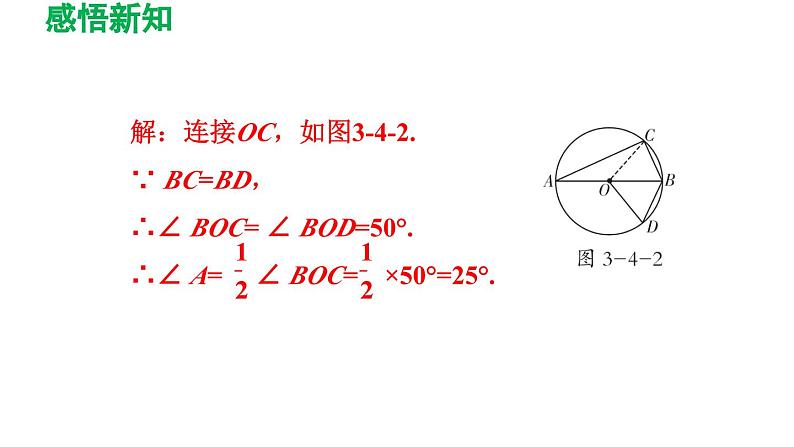
如图3-4-2，AB 是⊙ O 的直径， 弦BC=BD， 若∠ BOD=50°，求∠ A 的度数.
解题秘方：连接OC，将求BC所对的圆周角的度数转化为求BC所对的圆心角的度数来解.
解：连接OC，如图3-4-2.∵ BC=BD，∴∠ BOC= ∠ BOD=50°.∴∠ A= ∠ BOC= ×50°=25°.
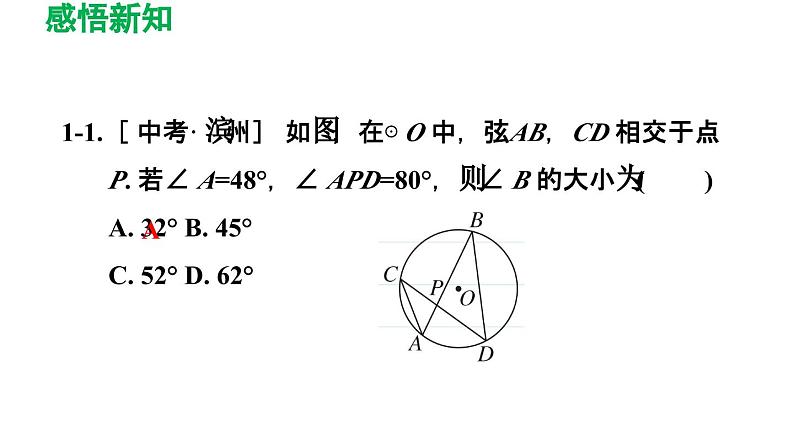
1-1.［ 中考· 滨州］ 如图，在⊙ O 中，弦AB，CD 相交于点P. 若∠ A=48°，∠ APD=80°，则∠ B 的大小为( )A. 32° B. 45°C. 52° D. 62°
1. 推论1 同弧或等弧所对的圆周角相等.
特别提醒“同弧或等弧”若改为“同弦或等弦”结论就不成立了.因为一条弦(非直径)所对的圆周角有两种情况：优弧上的圆周角和劣弧上的圆周角.
2. 推论2 (1)直径所对的圆周角是直角；(2)90°的圆周角所对的弦是直径.3.“五量关系”定理(拓展归纳)在同圆或等圆中，如果两个圆心角、两条弧、两条弧所对(或所含)的圆周角、两条弦、两条弦的弦心距中有一组量相等，那么它们所对应的其余各组量都分别相等.
如图3-4-3，A，P，B，C 是圆上的四个点，∠ APC=∠ CPB=60°．求证：△ ABC 是等边三角形.
解题秘方：紧扣“同弧所对的圆周角相等”解决.
证明：∵ A，P，B，C 是圆上的四个点，∴∠ ABC= ∠ APC，∠ CPB= ∠ BAC.又∵∠ APC= ∠ CPB=60°，∴∠ ABC= ∠ BAC=60°. ∴△ ABC 是等边三角形.
2-1. 如图， 以△ ABC的一边AB 为直径的半圆与其他两边AC，BC的交点分别为D，E，且DE = BE， 试判断△ ABC 的形状，并说明理由.
解：△ABC为等腰三角形．理由如下：如图，连接AE.∵DE＝BE，∴∠CAE＝∠BAE.∵AB为半圆的直径，∴∠AEB＝∠AEC＝90°.又∵AE＝AE，∴△ABE≌△ACE(ASA)．∴AB＝AC.∴△ABC为等腰三角形．
如图3-4-4，AB 是⊙ O 的直径，BD 是⊙ O 的弦，延长BD 到点C，使AC=AB. 求证：BD=CD.
解题秘方：紧扣“直径所对的圆周角是直角”，结合等腰三角形“三线合一”的性质求解.
证明：如图3-4-4，连接AD.∵ AB 是⊙ O 的直径，∴∠ ADB=90°，即AD ⊥ BC.又∵ AC=AB，∴ BD=CD.
3-1. 如图，AB 是⊙ O的直径， ∠ C=25 °，求∠ BAD 的度数.
解：∵AB为⊙O的直径，∴∠ADB＝90°.∵∠C＝25°，∴∠B＝∠C＝25°.∴∠BAD＝90°－∠B＝65°.
如图3-4-5，已知经过原点的⊙ P 与x 轴、y 轴分别交于A，B 两点，点C 是弧AB 上一点，则∠ ACB 的度数是( )A. 80° B. 90°C. 100° D. 无法确定
解题秘方：利用“直角所对的弦是直径”，结合“直径所对的圆周角是直角”求解.
解：连接AB，如图3-4-5.∵∠ AOB=90°，∴ AB 是⊙ P 的直径.∴∠ ACB=90°.
4-1. 如图，把直角三角板的直角顶点O 放在破损的圆玻璃镜的圆周上，两直角边与圆弧分别交于点M，N， 量得OM=8 cm，ON=6 cm，则该圆玻璃镜的半径是________ .
1. 圆内接四边形四边形ABCD 的四个顶点都在⊙ O 上，像这样的四边形叫做圆内接四边形，这个圆叫做四边形的外接圆.
特别解读每一个圆都有无数个内接四边形，但并不是所有的四边形都有外接圆，只有对角互补的四边形才有外接圆.
2. 圆周角定理的推论3圆内接四边形的对角互补.
[ 中考·常德]如图3-4-6，四边形ABCD 为⊙ O 的内接四边形，已知∠ BOD=100°，则∠ BCD 的度数为( )A. 50° B. 80°C. 100° D. 130°
解题秘方：将所求角的度数转化为求圆内接四边形对角的度数.
解：∵∠ BAD 与∠ BOD 是同弧所对的圆周角和圆心角，∴∠ BAD= ∠ BOD= ×100°=50°.又∵四边形ABCD 为⊙ O 的内接四边形，∴∠ BCD+ ∠ BAD=180°.∴∠ BCD=180°－∠ BAD=180°－50°=130°.
5-1.［ 中考· 镇江］ 如图， 四边形ABCD 是半圆的内接四边形，AB是直径，DC = CB，若∠ C=110°，则∠ ABC的度数等于( ) A. 55° B. 60°C. 65° D. 70°