初中数学北师大版八年级下册3 线段的垂直平分线背景图课件ppt

这是一份初中数学北师大版八年级下册3 线段的垂直平分线背景图课件ppt，共43页。PPT课件主要包含了逐点学练，本节小结，作业提升，本节要点，学习流程，知识点，1BEDE，∠APB＝2∠ACB，线段的垂直平分线等内容，欢迎下载使用。
线段垂直平分线的性质定理线段垂直平分线的判定定理三角形三条边的垂直平分线的性质定理用尺规作已知直线(或线段)的垂线
线段垂直平分线的性质定理
1. 性质定理 线段垂直平分线上的点到这条线段两个端点的距离相等.条件：点在线段的垂直平分线上.结论：这个点到线段两个端点的距离相等.
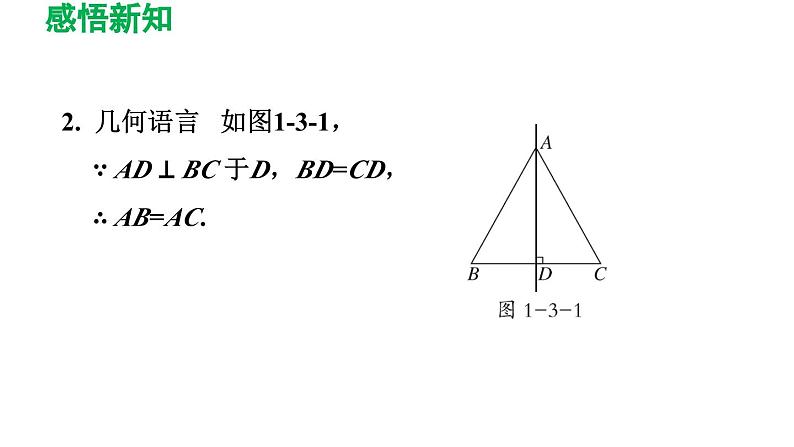
2. 几何语言 如图1-3-1，∵ AD ⊥ BC 于D，BD=CD，∴ AB=AC.
3. 线段垂直平分线的性质与角平分线的性质的联系与区别联系：两者都可以直接得到两条线段相等.区别：前者指的是点到点的距离，后者指的是点到直线的距离.
特别解读♦线段的垂直平分线的性质中的“距离”是“该点与这条线段两个端点的距离”.♦用线段的垂直平分线的性质可直接证明线段相等，不必再用三角形全等来证明，因此它为证明线段相等提供了新方法.
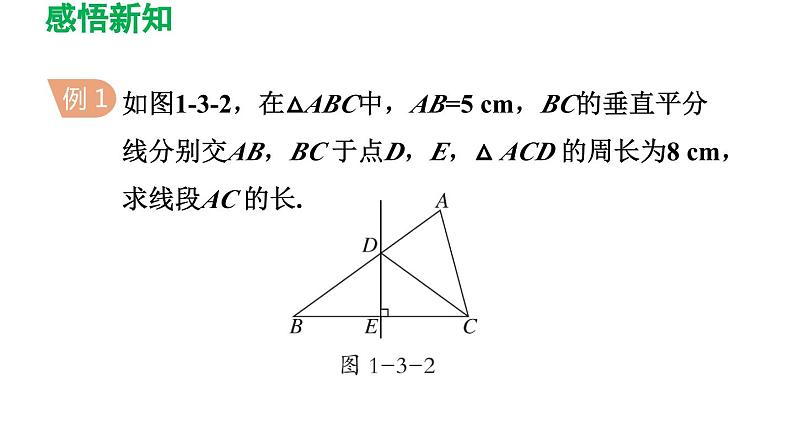
如图1-3-2，在△ABC中，AB=5 cm，BC的垂直平分线分别交AB，BC 于点D，E，△ ACD 的周长为8 cm，求线段AC 的长.
解题秘方：利用线段的垂直平分线的性质将要求的线段向已知条件转化.
解：∵ DE 为BC 的垂直平分线，∴ CD=BD.∴ △ ACD 的周长=AC+AD+CD=AC+AD+BD=AC+AB=8 cm.∵ AB=5 cm，∴ AC=3 cm.
1-1. 如图，AB所在直线是CD的垂直平分线，若AC=2.3 cm，BD=1.6 cm， 则四边形ACBD的周长是( )3.9 cm 7.8 cm3.2 cm 4.6 cm
线段垂直平分线的判定定理
1. 判定定理 到一条线段两个端点距离相等的点，在这条线段的垂直平分线上.条件：点到线段两个端点距离相等.结论：点在线段的垂直平分线上.
2. 几何语言 如图1-3-3，∵ AB=AC，∴点A 在线段BC 的垂直平分线上.
特别解读♦用定义法证明一个点在一条线段的垂直平分线上，思路有两种：一是作垂直，证平分；二是取中点，证垂直.♦用判定定理证明线段的垂直平分线，必须证明两个点在线段的垂直平分线上.
如图1-3-4，AD 为∠ BAC的平分线，交BC于点D，AE=AF，请判断线段AD 所在的直线是否为线段EF 的垂直平分线. 若是，请给予证明；若不是，请说明理由.
解题秘方：紧扣线段的垂直平分线的判定，证明直线AD上的点A 和点D 到线段EF 的两个端点的距离相等即可.
解：线段AD 所在的直线是线段EF 的垂直平分线. 证明：如图1-3-4，连接DE，DF.∵ AD 是∠ BAC 的平分线，∴∠ EAD= ∠ FAD.在△ AED 和△ AFD 中， AE=AF， ∠ EAD= ∠ FAD， AD=AD，
∴△ AED ≌△ AFD(SAS).∴ DE=DF.∴点D 在线段EF 的垂直平分线上.∵ AE=AF，∴点A 在线段EF 的垂直平分线上.∴线段AD 所在的直线是线段EF 的垂直平分线.
切忌只证明一个点在线段的垂直平分线上，就说过该点的直线是线段的垂直平分线.
教你一招：判断线段垂直平分线的两种方法 一是定义法，二是判定定理. 一般习惯用定义法进行判断，而利用判定定理判定一条直线是线段的垂直平分线时，一定要证明直线上有两点到线段两个端点的距离相等.
2-1. 如图，AB=AD，BC=DC， 点E 是AC上一点. 求证：
证明：连接BD.∵AB＝AD，∴点A在线段BD的垂直平分线上．又∵BC＝DC，∴点C在线段BD的垂直平分线上．∴AC所在的直线是线段BD的垂直平分线．∵点E是AC上一点，∴BE＝DE.
(2)∠ ABE= ∠ ADE.
证明：易知四边形ABCD是以直线AC为对称轴的轴对称图形，∴∠ABE＝∠ADE.
三角形三条边的垂直平分线的性质定理
性质定理 三角形三条边的垂直平分线相交于一点，并且这一点到三个顶点的距离相等.
特别解读因为三角形任意两条边的垂直平分线一定交于一点，所以要证明三角形三条边的垂直平分线的性质，只要证明这个交点在第三条边的垂直平分线上即可.该性质综合了线段垂直平分线的性质定理和判定定理，是这两个定理的升华，同时也给出了判定三线共点的一种特殊方法.
符号语言 如图1-3-5，∵直线MN，EF，PQ分别垂直平分BC，AB，AC，∴直线MN，EF，PQ 相交于一点O，且OA=OB=OC.
拓展 几种三角形三条边的垂直平分线交点的情况如图1-3-6.
如图1-3-7，OE，OF 所在直线分别是△ ABC 中AB，AC 边的垂直平分线，∠ OBC，∠ OCB 的平分线相交于点I，试判断OI 与BC 的位置关系，并给予证明.
解题秘方：根据三角形三边的垂直平分线相交于一点，三个内角的平分线也相交于一点，这两条性质进行证明.
解：OI⊥BC. 证明如下：如图1-3-7，延长OI 交BC 于点M.∵ OE 垂直平分AB，OF 垂直平分AC，∴ O 点在BC 的垂直平分线上.∴ OB=OC.
又∵ BI 平分∠ OBC，CI 平分∠ OCB，∴ OI 平分∠ BOC，即∠ BOI= ∠ COI.在△ BOM 和△ COM 中， OB=OC， ∠BOM=∠COM， OM=OM，∴△ BOM ≌△ COM(SAS). ∴∠ BMO= ∠ CMO.∵∠BMO+∠CMO=180°，∴∠BMO=∠CMO=90°，即OI⊥BC.
3-1. 如图， 点P为△ ABC三边垂直平分线的交点，∠PAC= 20°，∠PCB=30°.
(1)求∠ PAB 的度数；
(2)直接写出∠ APB与∠ ACB 的数量关系：___________________.
用尺规作已知直线(或线段)的垂线
归纳总结作图题的一般思路：1. 假设所求作的图形已作出，画出草图；2. 在草图上标出已知的边、角的对应位置及规定的交点字母；3. 从草图中找出可作的基本图形，确定作图顺序；4. 按确定的顺序作出所求作的图形.
如图1-3-8，已知线段a.
解题秘方：紧扣尺规作图作线段垂直平分线及过直线上一点作已知直线的垂线的步骤作出三角形，并按提供的数据求高.
解：作图如图1-3-9，△ ABC 即为所求.
(2)若在(1)作出的Rt △ ABC中，AB=4 cm，求AC边上的高.
4-1. 已知△ ABC(如图).(1)用尺规作AB 边上的高.
解：如图所示，线段CE即为所求．
(2)用尺规作BC 边的垂直平分线. (不写作法，保留作图痕迹)
解：如图所示，直线MN即为所求．