初中数学第六章 特殊平行四边形1 菱形的性质与判定多媒体教学ppt课件

这是一份初中数学第六章 特殊平行四边形1 菱形的性质与判定多媒体教学ppt课件，共21页。PPT课件主要包含了对角线，菱形的四条边相等，对称性，菱形是轴对称图形，菱形是中心对称图形，知识回顾，菱形的定义，菱形的性质，想一想，定义法等内容，欢迎下载使用。
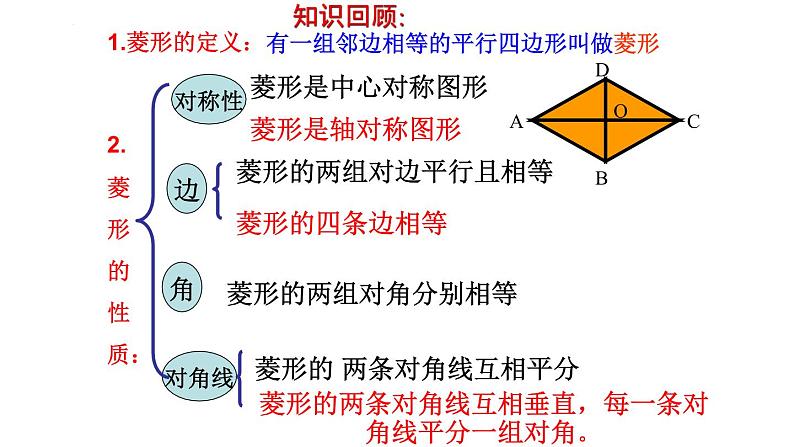
菱形的 两条对角线互相平分
菱形的两组对边平行且相等
菱形的两组对角分别相等
菱形的两条对角线互相垂直，每一条对角线平分一组对角。
有一组邻边相等的平行四边形叫做菱形
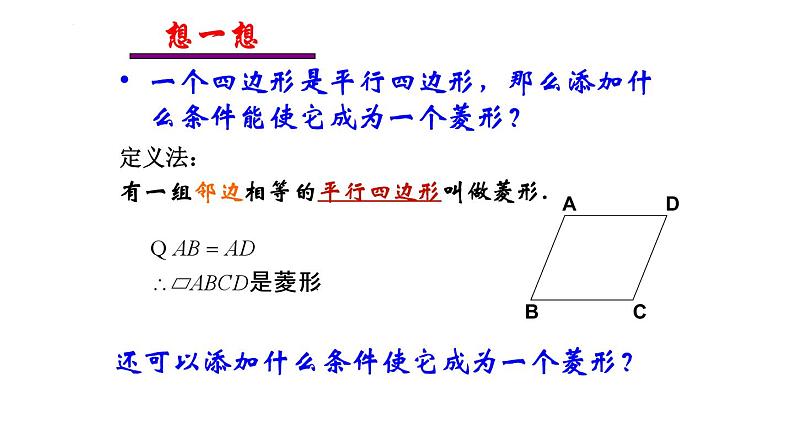
一个四边形是平行四边形，那么添加什么条件能使它成为一个菱形？
有一组邻边相等的平行四边形叫做菱形.
还可以添加什么条件使它成为一个菱形？
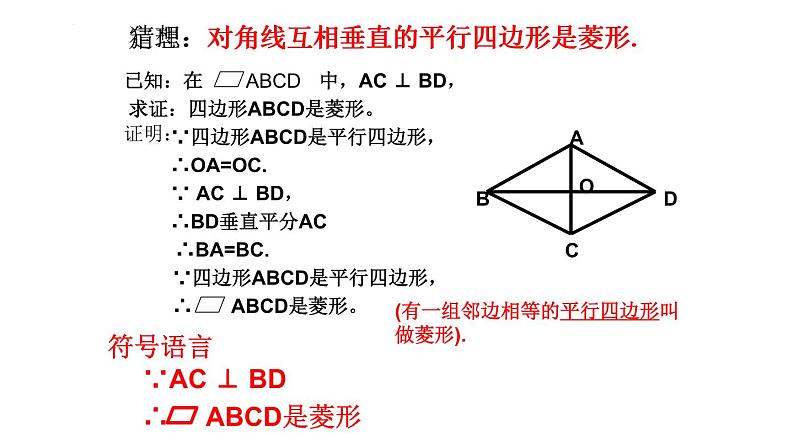
猜想：对角线互相垂直的平行四边形是菱形.
求证：四边形ABCD是菱形。
∴ ABCD是菱形。
∵四边形ABCD是平行四边形，
定理：对角线互相垂直的平行四边形是菱形.
(有一组邻边相等的平行四边形叫做菱形).
∴ ABCD是菱形
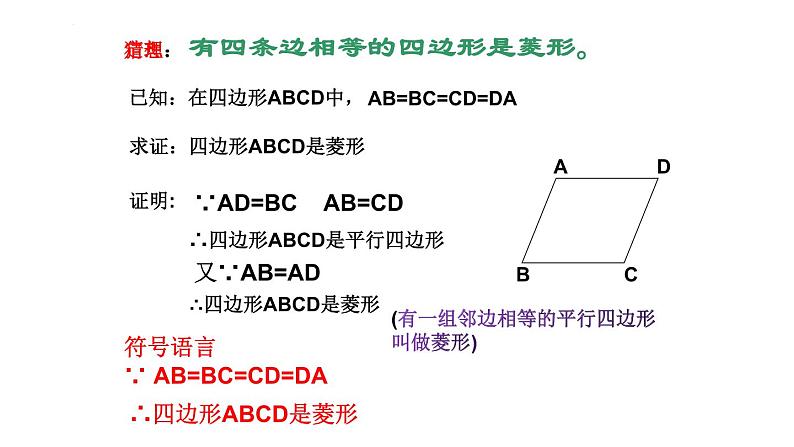
猜想： 有四条边相等的四边形是菱形。
∴四边形ABCD是平行四边形
已知：在四边形ABCD中，
AB=BC=CD=DA
求证：四边形ABCD是菱形
∴四边形ABCD是菱形
(有一组邻边相等的平行四边形叫做菱形)
∵ AB=BC=CD=DA
∵AD=BC AB=CD
定理： 有四条边相等的四边形是菱形。
有一组邻边相等的平行四边形是菱形.
对角线互相垂直的平行四边形是菱形.
有四条边相等的四边形是菱形.
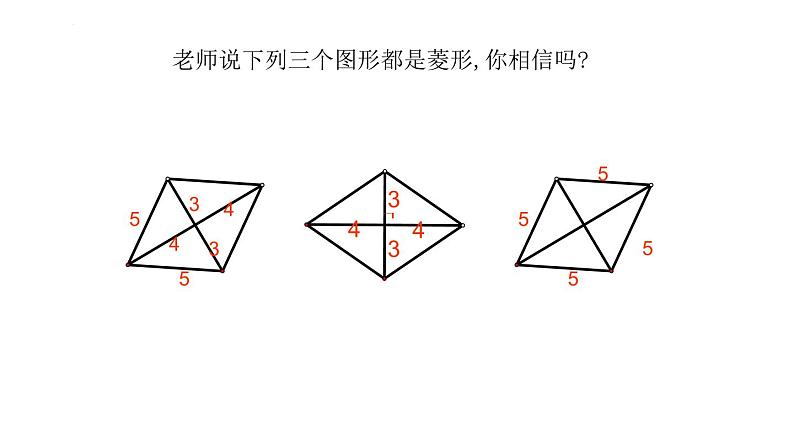
老师说下列三个图形都是菱形,你相信吗?
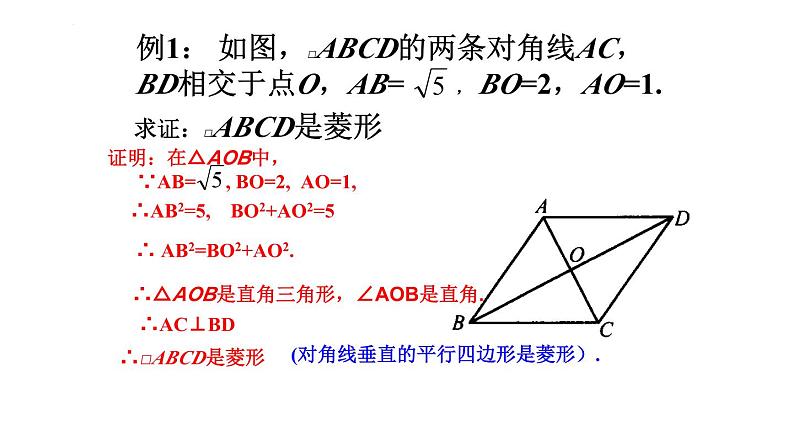
求证：□ABCD是菱形
∴□ABCD是菱形
(对角线垂直的平行四边形是菱形）.
证明：在△AOB中， ∵AB= , BO=2, AO=1,
∴AB2=5, BO2+AO2=5
∴ AB2=BO2+AO2.
∴△AOB是直角三角形，∠AOB是直角.
例2：已知：如图，四边形ABCD的对角线AC的垂直平分线与AD,AC,BC分别交于点E、O、F，且AD∥BC求证：四边形AFCE是菱形.
∵EF是AC的垂直平分线∴AE=CE,AO=CO
∵AD∥BC∴∠1=∠2
在△AOE和△COF中
∴△AOE≌△COF（ASA）
∴四边形AFCE是平行四边形
∴四边形AFCE是菱形
五、对应训练1.下列四边形不是菱形的是（ ） A.一组邻边相等的平行四边形 B.对角线互相垂直的四边形 C.对角线互相垂直平分的四边形 D.一条对角线平分一组对角的平行四边形2.四边形ABCD是平行四边形，下列条件：①AC⊥BD②∠BAD=90°③CD=BC ④AB⊥AC其中能单独判定平行四边形ABCD是菱形的是（ ）A.①③ B.②③ C.③④ D.②
3.已知E是□ABCD的边CD上的一点，且DE=AD,过点E作EF∥AD,交AB于点F，四边形AFED是菱形吗？为什么？
答：四边形AFED是菱形
∵四边形ABCD是平行四边形
∴四边形AFED是平行四边形
∴四边形AFED是菱形
六、当堂检测1.如图，四边形ABCD满足下列条件( )时，它是一个菱形A.AB=BC=CD=AC B.∠1=∠2=∠3=∠4C.AB=CD,AC⊥BD D.AO=CO,BO=DO,AB=CD
2.在△ABC中，AB≠AC，D是BC上一点，DE∥CA，交AB于E，DF∥BA交AC于点F，连接AD，要使四边形AEDF是菱形，只需添加条件（ ） A.AD⊥BC B.∠BAD＝∠CAD C.BD=DC D.AD=BC
4. 已知：如图，在菱形ABCD中，对角线AC与BD相交于点O，点E、F、G、H分别是OA、OB、OC、OD的中点.
求证：四边形EFGH是菱形.
∵E、F为OA、OB的中点∴EF为△OAB的中位线
∴FE= AB
FG= BC
GH= CD
HE= AD
又∵四边形ABCD为菱形∴AB=BC=CD=DA
∴EF=FG=GH=HE∴四边形EFGH为菱形
如图，△ABC中，AB=AC，AD是∠BAC的平分线，E为AD延长线上一点，CF∥BE交AD于F,连接BF、CE.求证：四边形BECF是菱形。