



还剩12页未读,
继续阅读
初中数学鲁教版 (五四制)八年级下册第六章 特殊平行四边形2 矩形的性质与判定示范课课件ppt
展开
这是一份初中数学鲁教版 (五四制)八年级下册第六章 特殊平行四边形2 矩形的性质与判定示范课课件ppt,共20页。PPT课件主要包含了平行四边形的性质,温故知新,矩形的定义,矩形的一般性质,矩形特殊的性质,从角上看,从对角线上看,想一想1,探索矩形的对称性,想一想等内容,欢迎下载使用。
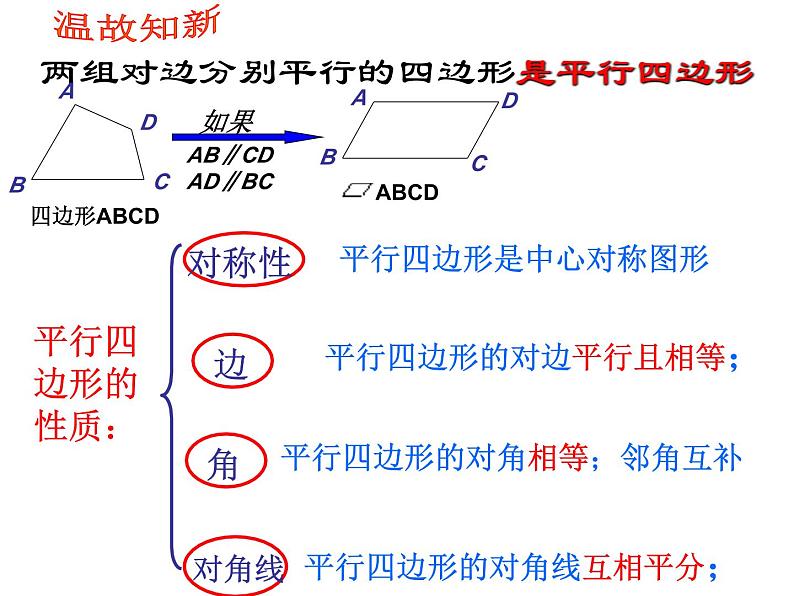
两组对边分别平行的四边形是平行四边形
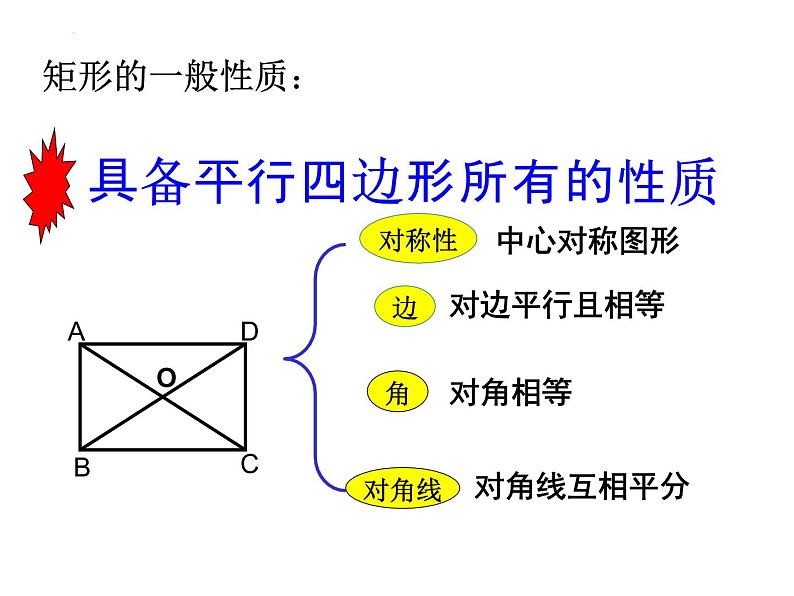
平行四边形的对边平行且相等;
平行四边形的对角相等;邻角互补
平行四边形的对角线互相平分;
平行四边形是中心对称图形
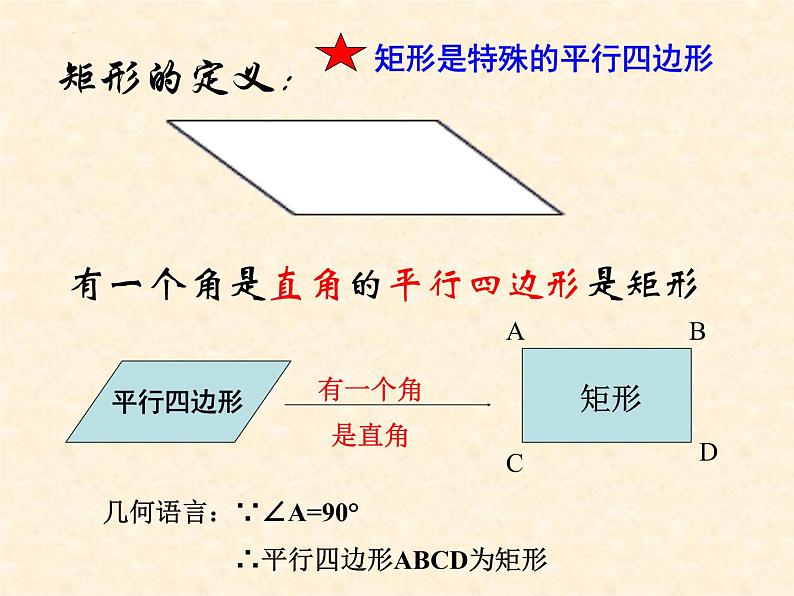
有一个角是直角的平行四边形是矩形
几何语言:∵∠A=90° ∴平行四边形ABCD为矩形
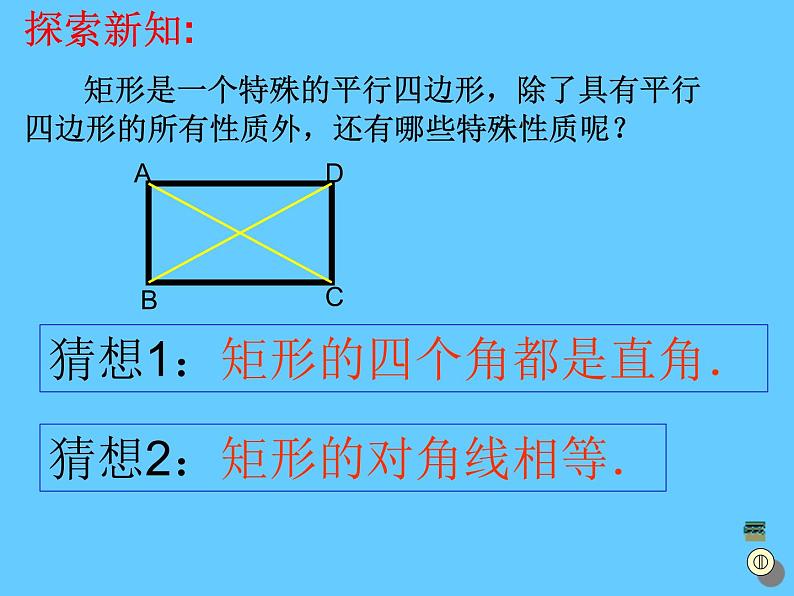
探索新知: 矩形是一个特殊的平行四边形,除了具有平行四边形的所有性质外,还有哪些特殊性质呢?
猜想1:矩形的四个角都是直角.
猜想2:矩形的对角线相等.
求证:矩形的四个角都是直角.
已知:如图,四边形ABCD是矩形
求证:∠A=∠B=∠C=∠D=90°
证明: ∵四边形ABCD是矩形
∴ ∠A=∠C ∠B = ∠D AD∥BC ∴∠A +∠B = 180°
∴ ∠A=∠B=∠C=∠D=90°即矩形的四个角都是直角
性质定理1:矩形的四个角都是直角
∵四边形ABCD为矩形
∴∠A=∠B=∠C=∠D=90°
已知:如图,四边形ABCD是矩形 求证:AC = BD
证明:∵四边形ABCD为矩形
∴∠ABC = ∠DCB = 90°
∴AC = BD 即矩形的对角线相等
求证:矩形的对角线相等
在△ABC与△DCB中
性质定理2:矩形的对角线相等
几何语言:∵四边形ABCD为矩形
矩形的四个角都是直角.
矩形的两条对角线相等.
矩形ABCD的对角线AC、BD相交于点O,图中有多少个直角三角形?有多少个等腰三角形? 有多少对全等三角形?
矩形 问题
直角三角形和等腰三角形 问题
Rt△ABC,Rt△BCD,Rt△ADB,Rt△DAB
△OAB,△OBC,△OCD,△OAD
如图,矩形ABCD的对角线AC与BD相交于点O,那么BO是Rt△ABC斜边AC的 线,它与AC有什么大小关系?由此你能得到什么结论?
由此可得推论: 直角三角形斜边上的中线等于斜边的一半
矩形是中心对称图形,又是轴对称图形
矩形是轴对称图形吗?对称轴有几条?
例1如图,在矩形ABCD中,两条对角线相交于点O,∠AOD=120°,AB=2.5,求矩形对角线的长.
∵∠AOD=120°,∴∠AOB=180°﹣∠AOD=180°﹣120°=60°,∴△AOB是等边三角形,∴OA=AB=2.5,∴AC=2OA=2×2.5=5.
1.矩形具有而平行四边形不具有的性质是( ) A、两组对边分别平行 B、对角相等 C、对角线互相平分 D、对角线相等
2.直角三角形斜边上的高与中线分别是5cm和6cm,则它的面积是 .
4.一个矩形的对角线长为2,对角线与一边的夹角是45°,则矩形的周长是 。
3.如右图,矩形ABCD的两条对角线相交于点O,它们的长度和为20cm,且AB的长为6cm,那么△ABC的周长是 .
5.如图,矩形ABCD,CE//BD交AB的延长线于点E, 判断△ACE的形状并加以证明.
∴AC=CE,∴△ACE是等腰三角形.
解:△ACE是等腰三角形,理由如下:
∵四边形ABCD是矩形,∴AC=BD,CD∥AB,即DC∥BE,
∵BD∥CE,∴四边形DCEB是平行四边形,
我收获,我成长,我快乐
1:矩形的四个角都是直角
3:矩形既是轴对称图形也是中心对称图形
直角三角形斜边上的中线等于斜边的一半
1.下列性质中,矩形不一定具有的是( )A、对角线相等 B、 四个角都相等 C、对角线垂直 D、是轴对称图形2.矩形ABCD的对角线AC、BD交于点O,AC=8cm,∠AOD=120°,则BC的长为 .3. 如图,在Rt△ABC中,CD是斜边AB的中线,CE是高.∠1=30°,则∠2= .
4.已知矩形ABCD,AB=2cm,AD=4cm,过对角线BD的中点O做BD的垂直平分线EF,分别交AD、BC于点E、F,求AE的长.
∵EF垂直平分BD∴ED=EB
设AE=xcm,则DE=EB=(4-x)cm
七、拓展提升1.如右图所示,矩形ABCD中,AE平分∠BAD交BC于E,∠CAE=15°,则下面的结论:①△ODC是等边三角形;②BC=2AB;③∠AOE=135°;④S△AOE=S△COE,其中正确结论有( )A.1个 B.2个 C.3个 D.4个
两组对边分别平行的四边形是平行四边形
平行四边形的对边平行且相等;
平行四边形的对角相等;邻角互补
平行四边形的对角线互相平分;
平行四边形是中心对称图形
有一个角是直角的平行四边形是矩形
几何语言:∵∠A=90° ∴平行四边形ABCD为矩形
探索新知: 矩形是一个特殊的平行四边形,除了具有平行四边形的所有性质外,还有哪些特殊性质呢?
猜想1:矩形的四个角都是直角.
猜想2:矩形的对角线相等.
求证:矩形的四个角都是直角.
已知:如图,四边形ABCD是矩形
求证:∠A=∠B=∠C=∠D=90°
证明: ∵四边形ABCD是矩形
∴ ∠A=∠C ∠B = ∠D AD∥BC ∴∠A +∠B = 180°
∴ ∠A=∠B=∠C=∠D=90°即矩形的四个角都是直角
性质定理1:矩形的四个角都是直角
∵四边形ABCD为矩形
∴∠A=∠B=∠C=∠D=90°
已知:如图,四边形ABCD是矩形 求证:AC = BD
证明:∵四边形ABCD为矩形
∴∠ABC = ∠DCB = 90°
∴AC = BD 即矩形的对角线相等
求证:矩形的对角线相等
在△ABC与△DCB中
性质定理2:矩形的对角线相等
几何语言:∵四边形ABCD为矩形
矩形的四个角都是直角.
矩形的两条对角线相等.
矩形ABCD的对角线AC、BD相交于点O,图中有多少个直角三角形?有多少个等腰三角形? 有多少对全等三角形?
矩形 问题
直角三角形和等腰三角形 问题
Rt△ABC,Rt△BCD,Rt△ADB,Rt△DAB
△OAB,△OBC,△OCD,△OAD
如图,矩形ABCD的对角线AC与BD相交于点O,那么BO是Rt△ABC斜边AC的 线,它与AC有什么大小关系?由此你能得到什么结论?
由此可得推论: 直角三角形斜边上的中线等于斜边的一半
矩形是中心对称图形,又是轴对称图形
矩形是轴对称图形吗?对称轴有几条?
例1如图,在矩形ABCD中,两条对角线相交于点O,∠AOD=120°,AB=2.5,求矩形对角线的长.
∵∠AOD=120°,∴∠AOB=180°﹣∠AOD=180°﹣120°=60°,∴△AOB是等边三角形,∴OA=AB=2.5,∴AC=2OA=2×2.5=5.
1.矩形具有而平行四边形不具有的性质是( ) A、两组对边分别平行 B、对角相等 C、对角线互相平分 D、对角线相等
2.直角三角形斜边上的高与中线分别是5cm和6cm,则它的面积是 .
4.一个矩形的对角线长为2,对角线与一边的夹角是45°,则矩形的周长是 。
3.如右图,矩形ABCD的两条对角线相交于点O,它们的长度和为20cm,且AB的长为6cm,那么△ABC的周长是 .
5.如图,矩形ABCD,CE//BD交AB的延长线于点E, 判断△ACE的形状并加以证明.
∴AC=CE,∴△ACE是等腰三角形.
解:△ACE是等腰三角形,理由如下:
∵四边形ABCD是矩形,∴AC=BD,CD∥AB,即DC∥BE,
∵BD∥CE,∴四边形DCEB是平行四边形,
我收获,我成长,我快乐
1:矩形的四个角都是直角
3:矩形既是轴对称图形也是中心对称图形
直角三角形斜边上的中线等于斜边的一半
1.下列性质中,矩形不一定具有的是( )A、对角线相等 B、 四个角都相等 C、对角线垂直 D、是轴对称图形2.矩形ABCD的对角线AC、BD交于点O,AC=8cm,∠AOD=120°,则BC的长为 .3. 如图,在Rt△ABC中,CD是斜边AB的中线,CE是高.∠1=30°,则∠2= .
4.已知矩形ABCD,AB=2cm,AD=4cm,过对角线BD的中点O做BD的垂直平分线EF,分别交AD、BC于点E、F,求AE的长.
∵EF垂直平分BD∴ED=EB
设AE=xcm,则DE=EB=(4-x)cm
七、拓展提升1.如右图所示,矩形ABCD中,AE平分∠BAD交BC于E,∠CAE=15°,则下面的结论:①△ODC是等边三角形;②BC=2AB;③∠AOE=135°;④S△AOE=S△COE,其中正确结论有( )A.1个 B.2个 C.3个 D.4个













