数学八年级下册9.3 平行四边形同步测试题

这是一份数学八年级下册9.3 平行四边形同步测试题，文件包含专题913中心对称图形平行四边形全章十六类必考压轴题苏科版原卷版docx、专题913中心对称图形平行四边形全章十六类必考压轴题苏科版解析版docx等2份试卷配套教学资源，其中试卷共270页， 欢迎下载使用。
必考点1
平行四边形中边的关系运用
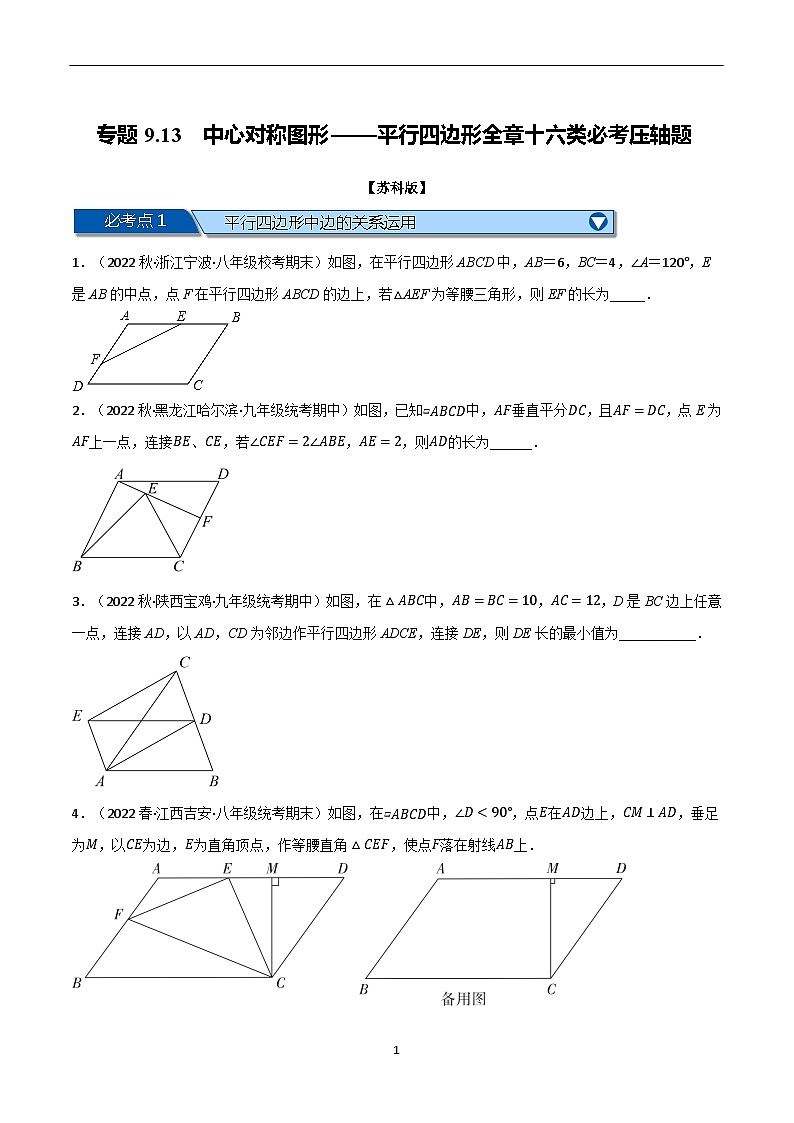
1．（2022秋·浙江宁波·八年级校考期末）如图，在平行四边形ABCD中，AB＝6，BC＝4，∠A＝120°，E是AB的中点，点F在平行四边形ABCD的边上，若△AEF为等腰三角形，则EF的长为_____．
【答案】33或3或572
【分析】△AEF为等腰三角形，分三种情况讨论，由等腰三角形的性质和30°直角三角形性质、平行四边形的性质可求解．
【详解】解：当AE=AF时，如图，过点A作AH⊥EF于H，
∵E是AB的中点，
∴AE=12AB=3，
∵AE=AF，AH⊥EF，∠A=120°，
∴∠AEF=∠AFE=30°，FH=EH，
∴AH=12AE=32，EH=3AH=332，
∴EF=2EH=33，
当AF=EF时，如图2，
过点A作AN⊥CD于N，过点F作FM⊥AB于M，
图2
∵在平行四边形ABCD中，AB=6，BC=4，∠A=120°，
∴AD=BC=4，∠ADC=60°，
∴∠DAN=30°，
∴DN=12AD=2，AN=3DN=23，
∵AB//CD，AN⊥CD，FM⊥AB，
∴AN=MF=23，
∵AF=EF，FM⊥AB，
∴AM=ME=32，
∴EF=ME2+MF2=12+94=572；
当AE=EF=3时，如图3，
图3
∴EF=3，
综上所述：EF的长为33或3或572．
【点睛】本题考查了平行四边形的性质，等腰三角形的性质，勾股定理，利用分类讨论思想解决问题是本题的关键．
2．（2022秋·黑龙江哈尔滨·九年级统考期中）如图，已知▱ABCD中，AF垂直平分DC，且AF=DC，点E为AF上一点，连接BE、CE，若∠CEF=2∠ABE，AE=2，则AD的长为______．
【答案】35
【分析】过点B作BM⊥CE于M，由平行四边形的性质得出AD=BC，AB=CD，AB∥CD，证明△BAE≌△BMEAAS，由全等三角形的性质得出AE=EM=2，AB=BM，证明Rt△AFD≌Rt△BMCHL，由全等三角形的性质得出FD=CM，设CF=FD=x，则AB=BM=2x，EF=2x−2，CE=2+x，由勾股定理列出方程可得出答案．
【详解】解：过点B作BM⊥CE于M，
∵AF垂直平分DC，
∴CF=DF，AF⊥CD，
∵四边形ABCD是平行四边形，
∴AD=BC，AB=CD，AB∥CD，
∴AB⊥AF，
∵∠BAE+∠AEM+∠BME+∠ABM=360°，
∴∠ABM+∠AEM=180°，
∵∠CEF+∠AEM=180°，
∴∠CEF=∠ABM=∠ABE+∠EBM，
又∵∠CEF=2∠ABE，
∴∠ABE=∠EBM，
∵BE=BE，∠BAE=∠BME=90°，
∴△BAE≌△BMEAAS，
∴AE=EM=2，AB=BM，
∵AB=CD=AF，
∴BM=AF，
在Rt△AFD和Rt△BMC中，
AD=BCAF=BM，
∴Rt△AFD≌Rt△BMCHL，
∴FD=CM，
设CF=FD=x，则AB=BM=2x，EF=2x−2，CE=2+x，
在Rt△CEF中，EF2+CF2=CE2，
∴2x−22+x2=2+x2，
解得x=3或x=0（舍去），
∴CM=3，BM=6，
∴BC＝CM2+BM2=32+62=35，
∴AD=35，
故答案为：35．
【点睛】本题考查了平行四边形的性质，全等三角形的判定与性质，勾股定理，熟练掌握平行四边形的性质是解题的关键．
3．（2022秋·陕西宝鸡·九年级统考期中）如图，在△ABC中，AB=BC=10，AC=12，D是BC边上任意一点，连接AD，以AD，CD为邻边作平行四边形ADCE，连接DE，则DE长的最小值为___________．
【答案】9.6
【分析】设AC,ED交于点O，过点O作OF⊥BC于点F，勾股定理求得OB，等面积法求得OF，根据垂线段最短，当点D与点F，重合时，OD最小，进而求得DE的最小值，即可求解．
【详解】设AC,ED交于点O，过点O作OF⊥BC于点F，如图所示，
在四边形ADCE中，AO=CO，EO=DO，
∵AB=BC=10，
∴BO⊥AC，
∵AC=12，
∴AO=CO=6,
在Rt△BOC中，BO=BC2−OC21=8，
∵S△OBC=12CO⋅BO=12BC⋅OF，
∴OF=4.8，
当点D与点F，重合时，OD最小，
∴ED的最小值为2OD=9.6．
故答案为：9.6．
【点睛】本题考查了平行四边形的性质，等腰三角形的性质，勾股定理，垂线段最短，掌握以上知识是解题的关键．
4．（2022春·江西吉安·八年级统考期末）如图，在▱ABCD中，∠DS2，则S3>S1；③若S3=2S1，则S4=2S2；④如果P点在对角线BD上，则S1:S4=S2:S3；⑤S1−S2=S3−S4，则P点一定在对角线BD上．
【答案】①④⑤
【分析】根据平行四边形的性质得AB=CD，AD=BC，设点P到AB，BC，CD，DA的距离分别是ℎ1，ℎ2，ℎ3，ℎ4，再根据三角形的面积公式整理判断①；然后根据三角形面积公式可判断②③；再根据两个等高的三角形面积的比等于底的比，得出S1:S4=S2:S3，判断④；最后根据已证关系式，得出S1=S2，S3=S4，判断⑤，综合即可得出答案．
【详解】解：∵四边形ABCD是平行四边形，
∴AB=CD，AD=BC．
设点P到AB，BC，CD，DA的距离分别是ℎ1，ℎ2，ℎ3，ℎ4，
则S1=12AB·ℎ1，S2=12BC·ℎ2，S3=12CD·ℎ3，S4=12AD·ℎ4．
∵12AB·ℎ1+12CD·ℎ3=12AB⋅ℎAB，12BC·ℎ2+12AD·ℎ4=12BC⋅ℎBC，
∴S平行四边形ABCD=AB⋅ℎAB=BC⋅ℎBC，
∴S2+S4=S1+S3，故①正确；
根据S4>S2只能判断ℎ4>ℎ2，不能判断ℎ3>ℎ1，即不能判断S3>S1，故②错误；
根据S3=2S1，能得出ℎ3=2ℎ1，不能得出ℎ4=2ℎ2，即不能判断S4=2S2，故③错误；
∵点P在对角线BD上，
∴S1:S4=PB:PD，S2:S3=PB:PD，
∴S1:S4=S2:S3，故④正确；
由S1−S2=S3−S4和S2+S4=S1+S3，得S1=S2，S3=S4，
∴点P一定在对角线在BD上，故⑤正确，
综上所述，正确的结论是①④⑤．
故答案为：①④⑤
【点睛】本题主要考查了平行四边形的性质、三角形的面积等，用平行四边形的面积表示出相应的两个三角形的面积的和是解本题的关键．
4．（2022秋·上海·七年级校考期末）小明在学习了中心对称图形以后，想知道平行四边形是否为中心对称图形．于是将一张平行四边形纸片平放在一张纸板上，在纸板上沿四边画出它的初始位置，并画出平行四边形纸片的对角线，用大头针钉住对角线的交点．将平行四边形纸片绕着对角线的交点旋转180°后，平行四边形纸片与初始位置的平行四边形恰好重合．通过上述操作，小明惊喜地发现平行四边形是中心对称图形，对角线的交点就是对称中心．请你利用小明所发现的平行四边形的这一特征完成下列问题：
(1)如图①，四边形ABCD是平行四边形，对角线AC、BD相交于点O．过点O的直线l与边AB、CD分别相交于点M、N，四边形AMND的面积与平行四边形ABCD的面积之比为___________；
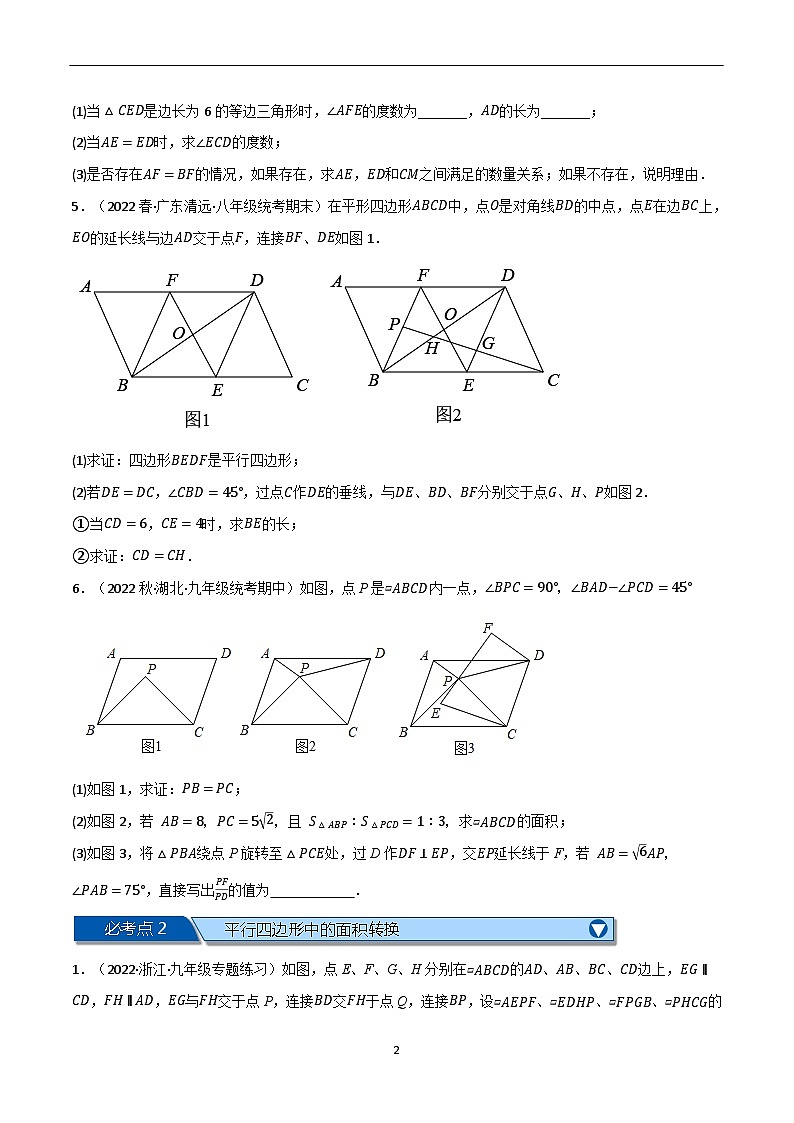
(2)如图②，这个图形是由平行四边形ABCD与平行四边形ECGF组成的，点E在边CD上，且B、C、G在同一直线上．
①请画出一条直线把这个图形分成面积相等的两个部分（不要求写出画法，但请标注字母并写出结论）；
②延长GF与边AD的延长线交于点K，延长FE与边AB交于点H．联结EB、EK、BK，如图③所示，当四边形AHED的面积为10，四边形CEFG的面积为2时，求三角形EBK的面积．
【答案】(1)1:2
(2)①图见解析，S四边形HGBM=S四边形AMND+S四边形NEFH；②三角形EBK的面积为4
【分析】（1）由四边形ABCD是平行四边形，对角线AC、BD相交于点O，得AB∥CD，OA=OC，从而得到∠MAO=∠NCO，即可证明出△MAO≌△NCO，同理可证明出△MBO≌△NDO，△COB≌△AOD，因此得到S△COB=S△AOD，S△MBO=S△NDO，S△MAO=S△NCO，又因为S四边形AMND=S△AMO+S△ADO+S△NDO，S四边形ABCD=S△AMO+S△CNO+S△MBO+S△ADO+S△NDO+S△COB，所以得到S四边形AMND=12S四边形ABCD，从而即可得到答案；
（2）①根据（1）中的结论画出图并写出相关结论即可；②由四边形ABCD是平行四边形得AB∥CD，AD∥BC，由四边形ECGF为平行四边形，得EC∥GF，EF∥CG，从而可得AK∥BG，AB∥GK，进而可得四边形ABGK为平行四边形，同理可得，四边形DEFK、四边形HBCE均为平行四边形，在根据平行四边形的面积与三角形的面积关系，即可得到三角形EBK的面积为．
【详解】（1）解：∵四边形ABCD是平行四边形，对角线AC、BD相交于点O，
∴AB∥CD，OA=OC，
∴∠MAO=∠NCO，
在△MAO和△NCO中
∠MAO=∠NCO∠AOM=∠CONAO=CO，
∴△MAO≌△NCO（AAS），
同理可得△MBO≌△NDO，△COB≌△AOD，
∴S△COB=S△AOD，S△MBO=S△NDO，S△MAO=S△NCO，
∵S四边形AMND=S△AMO+S△ADO+S△NDO，S四边形ABCD=S△AMO+S△CNO+S△MBO+S△ADO+S△NDO+S△COB，
∴S四边形AMND=12S四边形ABCD，
即四边形AMND的面积与平行四边形ABCD的面积之比为1:2，
故答案为：1:2；
（2）解：①根据（1）中的结论画出图如图所示，
平行四边形ABCD的对角线AC、BD相交于点O，平行四边形ECGF的对角线EG、CF相交于点Q，过点O、Q的直线l将图形分为面积相等的两个部分，直线l与AB相交于点M，直线l与GF相交于N，
其中S四边形MBCN=S四边形AMND，S四边形HGCN=S四边形NEFH，
∴S四边形HGBM=S四边形MBCN+S四边形HGCN=S四边形AMND+S四边形NEFH，
即S四边形HGBM=S四边形AMND+S四边形NEFH；
② ∵四边形ABCD是平行四边形，
∴AB∥CD，AD∥BC，
∵四边形ECGF为平行四边形，
∴EC∥GF，EF∥CG，
∴AK∥BG，AB∥GK，
∴四边形ABGK为平行四边形，
同理可得，四边形DEFK、四边形HBCE均为平行四边形，
∵S四边形AHED=10，S四边形CEFG=2，
∵S四边形ABGK=S四边形AHED+S四边形CEFG+S四边形BCEH+S四边形DEFK=10+2+S四边形BCEH+S四边形DEFK=12+S四边形BCEH+S四边形DEFK，
∴S△BGK=12S四边形ABGK=1212+S四边形BCEH+S四边形DEFK=6+12S四边形BCEH+12S四边形DEFK，
∵S△BCE=12S四边形BCEH，S△EFK=12S四边形DEFK，
∴S△EBK=S△BGK−S△BCE−S△EFK−S四边形CEFG=6+12S四边形BCEH+12S四边形DEFK−12S四边形BCEH−12S四边形DEFK−2=4，
∴三角形EBK的面积为4．
【点睛】本题考查了平行四边形的性质与判定的应用，熟练掌握平行四边形的性质与判定是解决问题的关键，难度较大，综合性较强．
5．（2022秋·吉林长春·八年级统考期末）定义：我们把三角形被一边中线分成的两个三角形叫做“朋友三角形”．性质：“朋友三角形”的面积相等．
例如：如图1，在△ABC中，如果AD是AB边上的中线，那么△ACD和△ABD是“朋友三角形”，则有S△ACD=S△ABD．
应用：如图2，在矩形ABCD中，点E在AD上，点F在BC上，AE=BF，AF与BE交于点O．
(1)求证：△AOE和△AOB是“朋友三角形”．
(2)如图3，在四边形ABCD中，∠ADC=90°，AD//BC，AD=DC=8，BC=12，点G在BC上，点E在AD上，DG与CE交于点F，GF=DF．
①求证：△DFE和△DFC是“朋友三角形”；
②连接AF，若△AEF和△DEF是“朋友三角形”，求四边形ABGF的面积．
(3)在△ABC中，∠B=30°，AB=8，点D在线段AB上，连接CD，△ACD和△BCD是“朋友三角形”，将△ACD沿CD所在直线翻折，得到△A′CD，若△A′CD与△ABC重合部分的面积等于△ABC面积的14，则△ABC的面积是________（请直接写出答案）．
【答案】(1)见解析
(2)①见解析；②四边形ABGF的面积为48
(3)8或83
【分析】（1）连接EF，根据四边形ABCD为矩形，可知AD∥BC，再借助AE=BF，可证明四边形ABFE为平行四边形，由平行四边形的性质“平行四边形的对角线相互平分”可知OE=OB，即AO是△ABE的中线，即可证明△AOE和△AOB是“朋友三角形”；
（2）①先证明△DFE≌△GFC，可推导EF=CF，即△DFE和△DFC是“朋友三角形”；②由△AEF和△DEF是“朋友三角形”，可知AE=DE=12AD=4，再借助∠ADC=90°，求得S△DCE=16，根据△DFE和△DFC是“朋友三角形”、△AEF和△DEF是“朋友三角形”、△DFE≌△GFC，可依次求得△AEF、△DEF、△DCF、△GFC的面积，最后由四边形ABGF的面积=S梯形ABCD−S△AEF−S△DFE−S△DFC−S△GFC求解即可；
（3）根据题意画出符合条件的两种情况：①证明四边形AD′CB是平行四边形，求出BC、A′D并推导∠ACB=90°，根据三角形面积公式求解即可；②求出高CQ、在求出△AD′C的面积，即可求出△ABC的面积．
（1）
证明：连接EF，
∵四边形ABCD为矩形，
∴AD∥BC，
∵AE=BF，
∴四边形ABFE为平行四边形，
∴OE=OB，即AO是△ABE的中线，
∴△AOE和△AOB是“朋友三角形”；
（2）
①证明：∵AD//BC，
∴∠EDF=∠CGF，
又∵GF=DF，∠DFE=∠GFC，
∴△DFE≌△GFC(ASA)，
∴EF=CF，
∴△DFE和△DFC是“朋友三角形”；
②解：∵△AEF和△DEF是“朋友三角形”，
∴AE=DE=12AD=4，
∵∠ADC=90°，
S△DCE=12DE⋅CD=12×4×8=16，
∵△DFE和△DFC是“朋友三角形”，
∴S△DFE=S△DFC=12S△DCE=8，
∵△DFE≌△GFC，
∴S△DFE=S△GFC=8，
∵△AEF和△DEF是“朋友三角形”，
S△AEF=S△DFE=8，
∴四边形ABGF的面积=S梯形ABCD−S△AEF−S△DFE−S△DFC−S△GFC
=12×(8+12)×8−8−8−8−8
=48；
（3）
分为两种情况：
①如图1所示：
∵S△ACD=S△BCD，
∴AD=BD=12AB=4，
∵沿CD折叠A和A′重合，
∴AD=A′D=12AB=12×8=4，
∵△A′CD与△ABC重合部分的面积等于△ABC面积的14，
∴S△DOC=14S△ABC=12S△BDC=12S△ADC=12S△′，
∴DO=OB，A′O=CO，
∴四边形A′DCB是平行四边形，
∴BC=A′D=4，
过B作BM⊥AC于M，
∵AB=8，∠BAC=30°，
∴BM=12AB=4=BC，
即C和M重合，
∴∠ACB=90°，由勾股定理得AC=82−42=43，
∴△ABC的面积=12×BC×AC=12×4×43=83；
②如图2所示：
∵S△ACD=S△BCD.
∴AD=BD=12AB，
∵沿CD折叠A和A′重合，
∴AD=′=12AB=12×8=4，
∵△A′CD与△ABC重合部分的面积等于△ABC面积的14，
∴S△DOC=14S△ABC=12S△BDC=12S△ADC=12S△A′DC，
∴DO=OA′，BO=CO，
∴四边形A′BDC是平行四边形，
∴A′C=BD=4，
过C作CQ⊥A′D于Q，
∵A′C=4，∠DA′C=∠BAC=30°，
∴CQ=12A′C=2，
∴S△ABC=2S△ADC=2S△′=2×12×′×CQ=2×12×4×2=8．
综上所述，△ABC的面积是8或83．
故答案为：8或83．
【点睛】本题主要考查了平行四边形的判定与性质、全等三角形的判定与性质、勾股定理、含30°角的直角三角形的性质等知识，是四边形综合题目，难度大，综合性强，解题关键是理解“朋友三角形”的概念及利用分类讨论的思想分析问题．
6．（2022秋·重庆大足·九年级统考期末）如图1，两个等腰直角三角形△ABC、△EDC的顶点C重合，其中∠ABC=∠EDC=90°，连接AE，取AE中点F，连接BF,DF．
(1)如图1，当B、C、D三个点共线时，请猜测线段BF、FD的数量关系，并证明；
(2)将△EDC绕着点C顺时针旋转一定角度至图2位置，根据“AE中点F”这个条件，想到取AC与EC的中点G、H，分别与点F相连，再连接BG,DH，最终利用△BGF≌△FHD（SAS）证明了（1）中的结论仍然成立．请你思考当△EDC绕着点C继续顺时针旋转至图3位置时，（1）中的结论是否仍然成立？若成立，请证明你的结论；若不成立，请说明理由；
(3)连接BD，在△EDC绕点C旋转一周的过程中，△BFD的面积也随之变化．若AC=52,CB=32，请直接写出△BFD面积的最大值．
【答案】(1)DF=BF，证明见解析
(2)成立，证明见解析
(3)32
【分析】（1）连接CF，由等腰直角三角形的性质证出∠ABF=∠CBF=45°，得出∠FBD=∠FDB，则可得出结论；
（2）取AC的中点M，CE的中点N，连接BM，FM，FN，DN，由三角形中位线定理证出四边形FNCM是平行四边形，得出∠FMC=∠FNC，证明△FMB≌△DNF（SAS），由全等三角形的性质得出BF=DF；
（3）当BD最大时，△BFD的面积最大，由等腰直角三角形的性质及三角形面积公式可得出答案．
【详解】（1）解：BF=DF．
连接CF，
∵△ABC和△EDC是等腰直角三角形，
∴∠ACB=∠DCE=45°，DC=DE，AB=BC，
∴∠ACE=90°，
∵F为AE的中点，
∴AF=CF=EF，
又∵DF=DF，
∴△DCF≌△DEF(SSS)，
∴∠CDF=∠EDF=45°，
同理△ABF≌△CBF(SSS)，
∴∠ABF=∠CBF=45°，
∴∠FBD=∠FDB，
∴DF=BF；
（2）解：成立，理由如下：
如图3，取AC的中点M，CE的中点N，连接BM，FM，FN，DN，
∵△ABC是等腰直角三角形，AM=MC，
∴∠MCB=∠MBC=45°，∠CMB=90°，BM=CM= 12 AC，
∵△DEC是等腰直角三角形，EN=NC，
∴∠DEN=∠DCN=45°，∠CND=90°，DN=CN= 12 CE，
∵F，N分别是AE和EC的中点，
∴FN是△AEC的中位线，
∴FN∥AC，FN= 12 AC，
∵F，M分别是AE和AC的中点，
∴FM是△AEC的中位线，
∴FM∥EC，FM= 12 EC，
∴BM= 12 AC=FN，DN= 12 EC=FM，
又∵FN∥AC，FM∥EC，
∴四边形FNCM是平行四边形，
∴∠FMC=∠FNC，
∴∠FMB+∠CMB=∠DNF+∠CND，
∴∠FMB=∠DNF，
∴△FMB≌△DNF（SAS），
∴BF=DF；
（3）解：过点F作FG⊥BD于点G，
由（2）知：△BFD是等腰直角三角形，
∴当BD最大时，△BFD的面积最大，
∵BD≤CB+CD，
∴当B、C、D共线时，BD最大=CB+CD=52+32=82，
∴S△BDF= 12 BD•GF= 12 ×82×42=32．
即△BFD面积的最大值是32．
【点睛】本题主要考查了等腰直角三角形的性质，全等三角形的判定与性质，平行四边形的判定与性质，三角形中位线定理等知识，熟练掌握旋转的性质及全等三角形的判定与性质是解题的关键．
必考点3
平行四边形中的角度转换
1．（2022春·江西新余·八年级新余四中校考期中）如图，平行四边形ABCD中，AE平分∠BAD，交BC于点E，且AB=AE，延长AB与DE的延长线交于点F．下列结论中：①△ABE是等边三角形：②△ABC≌△EAD；③AD=AF：④S△ABE=S△CDF；⑤S△ABE=S△CEF其中正确的是（ ）
A．①②③B．①④⑤C．①②⑤D．②③④
【答案】C
【分析】由AB=AE及平行四边形的性质、AE平分∠BAD，可得△ABE是等边三角形，即可判定①正确；由△ABE是等边三角形及平行四边形的性质可得△ABC≌△EAD，即可判定②正确；若点E是DF的中点，则可得AD=AF，否则AD与AF不相等，即可判定③错误；由S△ACD=S△CDF=S△ADE=S△ABC，可对④作出判断；由S△ACE=S△DCE及前一步的证明可判定⑤．
【详解】∵AB=AE
∴∠ABE=∠AEB
∵四边形ABCD是平行四边形
∴AD∥BC，AD=BC
∴∠DAE=∠AEB
∵AE平分∠BAD
∴∠DAE=∠BAE
∴∠BAE=∠AEB
∴∠BAE=∠AEB=∠ABE
∴△ABE是等边三角形
故①正确
∵△ABE是等边三角形
∴∠ABE=∠BAE=60°
∴ ∠ABE=∠DAE=60°
∵AB=AE，BC=AD
∴△ABC≌△EAD
故②正确
若点E是DF的中点，则可得AD=AF，否则AD与AF不相等
故③错误
∵四边形ABCD是平行四边形
∴AB∥CD，AD∥BC
∴S△ACD=S△CDF，S△ACD=S△ADE
∵△ABC≌△EAD
∴S△ADE=S△ABC
∴S△ACD=S△CDF=S△ADE=S△ABC
∵S△ABC=S△ABE+S△AEC>S△ABE
∴S△CDF>S△ABE
故④错误
∵AD∥BC
∴S△ACE=S△DCE
由④知，S△CDF=S△ABC
∴S△CDF−S△DCE=S△ABC−S△ACE
即S△CEF=S△ABE
故⑤正确
即正确的有①②⑤
故选：C.
【点睛】本题考查了平行四边形的性质，等边三角形的判定与性质，全等三角形的判定与性质，等底等高的两个三角形面积相等，其中平行四边形的性质是解题的关键．
2．（2022春·江苏南京·八年级统考期中）如图，在等边三角形ABC中，AB=4，P为AC上一点（与点A、C不重合），连接BP，以PA、PB为邻边作平行四边形PADB，则PD的取值范围是_______．
【答案】23≤PDCE−CB，
当C、B、E三点共线时（点E在CB的延长线上时），
BE=CE-CB，
综上所述BE≥CE-CB=5-3=2，
即BE≥2，
∴BE的最小值为2，
当BE=2时，BF2+BD2−BC2=4，
故答案为：4．
【点睛】本题考查了矩形的性质、旋转的性质、平行四边形的性质和勾股定理的应用，解决本题的关键是对以上性质的掌握是否熟练．
5．（2022春·辽宁沈阳·八年级统考期末）等边△ABC中，AB＝14．平面内有一点D，BD＝6，AD＝10， 则CD的长为_____．
【答案】219或16
【分析】分点D在△ABC的内部和点D在△ABC的外部两种情况，先利用等边三角形的性质可得BE=7,CE=73，再根据勾股定理可得BF=337，从而可得DG、CG的长，然后在Rt△CDG中，利用勾股定理即可得．
【详解】由题意，分以下两种情况：
（1）如图1，点D在△ABC的内部
过点C作CE⊥AB于点E，过点D作DF⊥AB于点F，作DG⊥CE于点G
则四边形DFEG是矩形
∴DG=EF,EG=DF
∵ △ABC是等边三角形，AB=14
∴BE=12AB=7,CE=32AB=73
设BF=x，则AF=AB−BF=14−x
在Rt△ADF中，DF2=AD2−AF2=100−(14−x)2
在Rt△BDF中，DF2=BD2−BF2=36−x2
则100−(14−x)2=36−x2
解得x=337
即BF=337
∴DG=EF=BE−BF=167,EG=DF=36−x2=1573
∴CG=CE−EG=73−1573=3473
在Rt△CDG中，CD=DG2+CG2=(167)2+(3473)2=219
（2）如图2，点D在△ABC的外部
过点C作CE⊥AB于点E，过点D作DF⊥AB于点F，作DG⊥CE，交CE延长线于点G
同理可得：CE=73,DG=EF=167,EG=DF=1573
∴CG=CE+EG=73+1573=6473
在Rt△CDG中，CD=DG2+CG2=(167)2+(6473)2=16
综上，CD的长为219或16
故答案为：219或16．
【点睛】本题考查了矩形的判定与性质、等边三角形的性质、勾股定理等知识点，依据题意，正确分两种情况讨论，并通过作辅助线，构造直角三角形是解题关键．
6．（2022秋·天津·九年级校考期末）在平面直角坐标系中，矩形OABC，O为原点，A3,0,B3,4,C0,4，将△OBC绕点B逆时针旋转，点O,C旋转后的对应点为O′,C′．
(1)如图（1），当∠CBC′=30°时，求C′的坐标；
(2)如图（2），当点O′恰好落在x轴上时，O′C′与AB交于点D．
①此时DB与DO′是否相等，说明理由；
②求点D的坐标；
(3)求△AO′C′面积的最大值．（直接写出答案即可）
【答案】(1)C′3−332,52
(2)①DB=DO′；②D3,78
(3)14
【分析】（1）如图①中，过点C′作C′H⊥BC于点H．解直角三角形求出BH，CH，可得结论；
（2）①此时DB与DO′相等，证明∠DBO′=∠DO′B即可；
②设DB=DO′=x，再利用勾股定理构建方程求出x即可；
（3）如图③中，当点C′值AB的延长线上时，△AO′C′的面积最大．
【详解】（1）如图①中，过点C′作C′H⊥BC于点H．
∵四边形OABC是矩形，B(3,4)，
∴AB=OC=4，BC=3，
在Rt△ BC′H中，∠BHC′=90°，∠HBC′=30°，
∴HC′=12BC′=32，BH=332，
∴CH=3−332，
∴C′3−332,52；
（2）①结论：DB=DO′．
理由：∵BO=BO′，BA⊥OO′，
∴∠OBA=∠ABO′，
∵AB∥OC，
∴∠ABO=∠COB=∠BO′C′，
∴∠DBO′=∠DO′B，
∴DB=DO′；
②∵BO=BO′，BA⊥OO′，
∴OA=AO′=3，
设BD=DO′=x，
在Rt△ADO′中，AD2+AO′2=O′D2，
∴(4−x)2+32=x2，
∴x=258，
∴AD=4−258=78，
∴D(3,78)．
（3）如图③中，当点C′值AB的延长线上时，此时点A到O′C′的距离最大，即△AO′C′的面积最大．
△AO′C′的面积的最大值=12×7×4=14．
【点睛】本题属于四边形综合题，考查了矩形的性质，解直角三角形，等腰三角形的判定和性质等知识，解题的关键是学会添加常用辅助线，构造直角三角形解决问题，学会利用参数构建方程解决问题．
必考点12
菱形中的全等三角形的构造
1．（2022春·山东济南·八年级统考期末）如图，菱形ABCD中，∠BAD=60°，AC与BD交于点O，E为CD延长线上一点，且CD=DE，连接BE，分别交AC，AD于点F、G，连接OG，则下列结论：
①OG=12AB；②S四边形ODGF>S△ABF；③由点A、B、D、E构成的四边形是菱形；④S△ACD=4S△BOG，其中正确的结论是（ ）
A．①②B．①②③C．①③④D．②③④
【答案】C
【分析】①由AAS证明△ABG≌△DEG，得出AG=DG，证出OG是△ABD的中位线，得出OG=12AB，①正确；
③先证明四边形ABDE是平行四边形，证出△ABD、△BCD是等边三角形，得出AB=BD=AD，因此OD=AG，得出四边形ABDE是菱形，③正确；
②连接FD，由等边三角形的性质和角平分线的性质得F到△ABD三边的距离相等，则S△BDF=S△ABF=2S△BOF=2S△DOF=S四边形ODGF，则S四边形ODGF=S△ABF，②错误；即可得出结论．
④∵连接CG，由O、G分别是AC，AD的中点，得到S△AOG=S△COG，S△ACG=S△DCG，则S△ACD＝4S△AOG，再由S△AOG＝S△BOG，得到S△ACD＝4S△BOG，故④正确；
【详解】∵四边形ABCD是菱形，
∴AB＝BC＝CD＝DA，AB∥CD，OA＝OC，OB＝OD，AC⊥BD，
∴∠BAG＝∠EDG，
∵CD＝DE，
∴AB＝DE，
在△ABG和△DEG中，
∠AGB=∠DGE∠BAG=∠EDGAB=DE，
∴△ABG≌△DEG（AAS），
∴AG＝DG，
∴OG是△ABD的中位线，
∴OG＝12AB，故①正确；
∵AB∥CE，AB＝DE，
∴四边形ABDE是平行四边形，
∵∠BCD＝∠BAD＝60°，
∴△ABD、△BCD是等边三角形，
∴AB＝BD＝AD，∠ODC＝60°，
∴平行四边形ABDE是菱形，故③正确；
∵连接CG，
∵O、G分别是AC，AD的中点，
∴S△AOG=S△COG，S△ACG=S△DCG，
∴S△ACD＝4S△AOG，
∵OG∥AB，
∴S△AOG＝S△BOG，
∴S△ACD＝4S△BOG，故④正确；
连接FD，如图：
∵△ABD是等边三角形，AO平分∠BAD，BG平分∠ABD，
∴F到△ABD三边的距离相等，
∴S△BDF＝S△ABF＝2S△BOF＝2S△DOF＝S四边形ODGF，
∴S四边形ODGF＝S△ABF，故②错误；
正确的是①③④，
故选C．
【点睛】本题考查了菱形的判定与性质、全等三角形的判定与性质、等边三角形的判定与性质、三角形中位线定理以及三角形面积等知识，综合运用以上知识是解题的关键．
2．（2022秋·浙江绍兴·八年级统考期末）如图，AB∥CD，AC平分∠BAD，BD平分∠ADC，AC和BD交于点E，F，G分别是线段AB和线段AC上的动点，且AF=CG，若DE=1，AB=2，则DF+DG的最小值为______．
【答案】22
【分析】先根据AC平分∠BAD，BD平分∠ADC，AB∥CD证明四边形ABCD是菱形．在AC上取点B'，使AB'=AB，连接FB'，作点D关于AB的对称点D'，连接D'F、DD'．作BH⊥CD于点H，作BM⊥DD'于点M，则△B'AF≌△DCG（SAS），得出B'F=DG，所以DF+DG=D'F+B'F，当B'、F、D'三点在同一直线上时，DF+DG=D'F+B'F取最小值为B'D'．再根据勾股定理求出B'D'即可．
【详解】解：连接BC，
∵AC平分∠BAD，BD平分∠ADC，AB∥CD，
∴∠DAC=∠BAC，∠ADB=∠CDB，∠AED=180°-180°÷2=90°，
∵AB∥CD，
∴∠DCA=∠BAC，
∴∠DCA=∠DAC，
∴DA=DC，
同理：DA=BA，
∴DC=AB，
∵AB∥CD，
∴四边形ABCD是平行四边形，
∵DA=DC，
∴四边形ABCD是菱形．
如图．在AC上取点B'，使AB'=AB，连接FB'，作点D关于AB的对称点D'，连接D'F、DD'．
作B'H⊥CD于点H，作B'M⊥DD'于点M．
∴DF=D'F，
∵AF=CG，∠B'AF=∠DCG，AB'=AB=CD，
∴△B'AF≌DCG（SAS），
∴B'F=DG，
∴DF+DG=D'F+B'F，
∴当B'、F、D'三点在同一直线上时，DF+DG=D'F+B'F取最小值为B'D'．
∵DE=1，AD=AB=2，
∴∠DAE=30°，∠ADE=60°，
∴AC=3AD=23，CB'=23-2，
∴B'H=12B'C=3-1，CH=3B'H=3-3，
∴DH=DC-CH=2-（3-3）=3−1，
∵四边形DHB′M是矩形
∴DM=B'H=3-1，MB′=DH=3−1,
∴D'M=DD'-DM=3AD-DM=23-（3-1）=3+1，
∴D'B'=MB′2+MD′2=(3−1)2+(3+1)2=22．
即DF+DG的最小值为22．
故答案为：22．
【点睛】本题考查了线段之和最小值问题，作辅助线推出△B'AF≌△DCG是解题的关键．
3．（2022春·黑龙江哈尔滨·八年级统考期末）在平行四边形ABCD中，∠BAD的平分线交边BC于点E，交DC的延长线于点F．
(1)如图1，求证：CE=CF；
(2)如图2，FG∥BC,FG=EC，连接DG、EG，当∠ABC=120°时，求证：∠BDG=60°；
(3)如图3，在（2）的条件下，当BE=2CE,AE=43时，求线段BD的长．
【答案】(1)见解析
(2)见解析
(3)BD=27
【分析】（1）根据角平分线的性质可得∠1=∠2，然后再运用平行四边形的性质说明∠2=∠3,∠1=∠F，进一步说明∠3=∠F，最后运用等边对等角即可证明结论；
（2）延长AB、FG交于点H，连接DH，可证得四边形AHFD是平行四边形，四边形AHFD是菱形，推出△FDH和△ADH都是等边三角形，再证明△DFG≌△DHB（SAS），得出∠FDG=∠HDB，进而证得结论；
（3）如图3，连接DE，根据平行四边形性质和角平分线性质可得∠BAE=∠AEB=180°−∠ABC2=30°，过点B作BM⊥AE于点M，可得EM=12AE=23，利用勾股定理求得AB=CD=BE=4，过点D作DN⊥BC于点N，结合勾股定理即可解答．
（1）
明：如图1：∵AF是∠BAD平分线．
∴∠1=∠2
∵ABCD是平行四边形．
∴AD∥BC,AB∥CD
∴∠2=∠3,∠1=∠F，
∴∠3=∠F，
∴CE=CF．
（2）
证明：如图2;延长AB、FG交于点H，连接DH，
∴FG∥CE，CE∥AD，
∴FH∥BC∥AD，
∵AH∥DF，
∴四边形AHFD是平行四边形，
∵∠DFA=∠FAB=∠DAF，
∴DA=DF，
∴四边形AHFD是菱形，
∴FD=FH，AD=AH，
∵∠ABC=120°，
∴∠DFH=∠DAH=60°，
∴△FDH和△ADH都是等边三角形，
∴∠DFG=∠DHB=∠FDH=60°，FD=HD，
∵四边形BCFH是平行四边形，
∴BH=CF，
∵FG=CE，CE=CF，
∴FG=BH，
在△DFG和△DHB中，
FG=BH∠GFD=∠BHDFD=HD
∴△DFG≌△DHB(SAS),
∴∠FDG=∠HDB,
∴∠BDG=∠HDB+∠HDG=∠FDG+∠HDG=∠FDH=60°．
（3）
解：如图3，连接DE，
∵四边形ABCD是平行四边形，
∴AB∥CD，AD∥BC，
∴∠DAE=∠AEB，∠DCB=180°-∠ABC=60°，
∵AE平分∠BAD，
∴∠BAE=∠DAE，
∴∠BAE=∠AEB=180°−∠ABC2=30°
过点B作BM⊥AE于点M
∴EM=12AE=23
在Rt△BME中
∵∠BEM=30°
∴BM=12BE
∵BE2−BM2=EM2
∴BE2−(12BE)2=(23)2，解得：BE=4
∵BE=2CE
∴CE=2
过点D作DN⊥BC于点N,则∠NDC=90°-∠DCB=30°
∴CN=12CD=2=CE
∴点N与点E重合
∴∠DEC=90°
∴DE2=CD2−CE2=42−22=12
∴BD=DE2+BE2=12+16=27 ．
【点睛】本题主要考查平行四边形的判定与性质、菱形的判定与性质、全等三角形的判定与性质、等边三角形的判定与性质、含30°的直角三角形性质、勾股定理等知识点，正确地作出辅助线是解答本题的关键．
4．（2022春·山东德州·八年级统考期末）如图1，在平面直角坐标系中，直线y=−34x+b分别与x轴、y轴交于点A、B，且点A的坐标为(8，0)，四边形ABCD是正方形．
(1)求b的值和点D的坐标；
(2)点M是线段AB上的一个动点（点A、B除外）．
①如图2，将△BMC沿CM折叠，点B的对应点是点E，连接ME并延长交AD边于点F，问△AMF的周长是否发生变化？若不变，求出其值；若变化，请说明理由；
②点P是x轴上一个动点，Q是坐标平面内一点，探索是否存在一个点P，使得以A、B、P、Q为顶点的四边形是菱形？若不存在，请说明理由；若存在，请直接写出点Q的坐标．
【答案】(1)b的值为6，点D的坐标为(14，8)
(2)①△AMF的周长不变，△AMF的周长为20；②存在，点Q的坐标为(0，−6)或(−10，6)或(10，6)或(254，6)
【分析】（1）将点A(8，0)代入y=−34x+b，即可求出b的值，从而即得出直线AB的解析式为y=−34x+6，进而即得出A(0，6)．过点D作DH⊥x轴于点H，由正方形的性质结合题意利用“AAS”易证△AOB≅△DHA，得出DH=OA=8，OH=OA+AH=14，即得出D(14，8)；
（2）①由折叠和正方形的性质可知BM=EM，CD=CE=4，∠CDF=∠CEF=90°，即易证△CDF≅△CEF(HL)，得出DF=EF．再由△AMF的周长=AM+ME+EF+AF=AM+BM+DF+AF=AB+AD，结合勾股定理即可求出答案；②分类讨论ⅰ当AP为菱形的对角线时，ⅱ当AQ为菱形的对角线时和ⅲ当AB为菱形的对角线时，根据菱形的性质结合图形即可求出答案．
【详解】（1）解：将点A(8，0)代入y=−34x+b，得0=−34×8+b，
解得：b=6，
∴直线AB的解析式为y=−34x+6，
当x=0，时y=6，
∴A(0，6)，
∴OB=6，OA=8．
如图，过点D作DH⊥x轴于点H，
∵四边形ABCD为正方形，
∴AB=AD，∠BAD=90°，
∴∠BAO+∠DAH=90°．
∵∠BAO+∠ABO=90°，
∴∠ABO=∠DAH．
又∵∠AOB=∠DHA=90°，
∴△AOB≅△DHA(AAS)，
∴DH=OA=8，AH=OB=6，
∴OH=OA+AH=14，
∴D(14，8)；
（2）解：①由折叠的性质可知BM=EM，BC=CE=4，∠CBM=∠CEM=90°，
∴CD=CE=4，∠CDF=∠CEF=90°，
又∵CF=CF，
∴△CDF≅△CEF(HL)
∴DF=EF．
∵△AMF的周长=AM+MF+AF，MF=ME+EF，
∴△AMF的周长=AM+ME+EF+AF=AM+BM+DF+AF=AB+AD．
∵OB=6，OA=8，
∴AB=OA2+OB2=10，
∴△AMF的周长=10+10=20，
故△AMF的周长不变，且为20；
②存在以A、B、P、Q为顶点的四边形是菱形，理由如下：
设P(t，0)，Q(x，y)．
分类讨论：ⅰ当AP为菱形的对角线时，如图菱形ABP1Q1，此时AB=BP1．
∵xA+xP=xQyB+yQ=yABP1=OB2+OP12，
即8+t=x6+y=010=62+t2，
解得：x1=16y1=−6t1=8（舍），x2=0y2=−6t2=−8；
即此时Q(0，-6)；
ⅱ当AQ为菱形的对角线时，如图菱形ABQ2P2和ABQ4P4，此时AB=AP2和AB=AP4．
同理可得：8+x=ty=610=8−t，
解得：x1=−10y1=6t1=−2，x2=10y2=6t2=18；
即此时Q(-10，6)或(10，6)；
ⅲ当AB为菱形的对角线时，如图菱形AQ3BP3，此时AP3=BP3．
同理可得8=t+xy=636+t2=8−t，
解得：x=254y=6t=74；
即此时Q(254，6)；
综上可知点Q的坐标为(0，−6)或(−10，6)或(10，6)或(254，6)时，以A、B、P、Q为顶点的四边形是菱形．
【点睛】本题考查正方形的性质，三角形全等的判定和性质，折叠的性质，勾股定理以及菱形的判定和性质等知识．正确的作出辅助线并利用数形结合的思想是解题关键．
5．（2022春·河南鹤壁·八年级鹤壁市外国语中学校考期末）如图，在平行四边形ABCD中，两条对角线相交于点O，EF经过点O且垂直于AC，分别与边AD，BC交于点F，E．
(1)求证：四边形AECF为菱形；
(2)若AD＝3，CD=2，且∠ADC＝45°，直接写出四边形AECF的面积．
【答案】(1)见解析
(2)54
【分析】（1）根据平行四边形、平行线的性质得出OA=OC，OB=OD，AD∥BC，进而得出∠FDO=∠EBO，由全等三角形的判定（角边角）得出△FDO≌△EBO，再利用全等三角形的性质得出OF=OE，最后根据菱形的判定及已知EF⊥AC即可证明．
（2）设辅助线CG⊥AD于点G，利用勾股定理得出CG的值，由（1）已知四边形AECF为菱形，根据菱形的性质设AF=t，则FG=2−t，CF=t，利用勾股定理建立等式求解得出t值，最后利用菱形的性质及三角形面积公式求解即可．
（1）
∵四边形ABCD是平行四边形，对角线AC，BD相交于点O，
∴OA=OC，OB=OD，AD∥BC．
∴∠FDO=∠EBO．
∵{∠FDO=∠EBO,OD=OB,∠DOF=∠BOE,
∴△FDO≌△EBO．
∴OF=OE．
∵EF⊥AC，且EF，AC互相平分，
∴四边形AECF为菱形．
（2）
如图，作CG⊥AD于点G，
∵AD＝3，CD=2，且∠ADC＝45°，∠CGD=∠CGF=90°，
∴∠ADC=∠GCD=45°．
∴CG=GD，△CGD是等腰直角三角形．
∵CG2+GD2=CD2，即2CG2=2，
∴CG=GD=1，AG=AD−GD=3−1=2．
∵由（1）已知四边形AECF是菱形，
∴AF=CF．
设AF=t，则FG=2−t，CF=t，
∵FG2+CG2=CF2，即(2−t)2+1=t2，
∴解得t=54．
∴AF=54．
∴S菱形AECF=2S△AFE=2×12AF⋅CG=2×12×54×1=54．
【点睛】本题考查菱形的判定与性质，平行四边形的性质，全等三角形的判定与性质，勾股定理等的理解与综合应用能力．对角线互相垂直平分的四边形是菱形．菱形四条边都相等．两角及其夹边分别相等的三角形全等．平行四边形的对边平行且相等；平行四边形的两条对角线互相平分．两全等三角形的对应边相等，对应角相等．灵活利用菱形的判定与性质，全等三角形的判定与性质，根据勾股定理建立等式关系是解本题的关键．
6．（2022春·江苏淮安·八年级统考期末）如图，平行四边形ABCD中，AB⊥AC，AC=2AB．对角线AC，BD相交于点O，将直线AC绕点O顺时针旋转β°0