初中数学苏科版八年级下册第9章 中心对称图形——平行四边形9.3 平行四边形测试题

这是一份初中数学苏科版八年级下册第9章 中心对称图形——平行四边形9.3 平行四边形测试题，文件包含重难点01平行四边形6种模型与解题方法原卷版docx、重难点01平行四边形6种模型与解题方法解析版docx等2份试卷配套教学资源，其中试卷共146页， 欢迎下载使用。

题型一：中点四边形 题型二：十字架模型
题型三：梯子模型 题型四：对角互补模型
题型五：与正方形有关三垂线 题型六：正方形与45°角的基本图
技巧方法
一、中点四边形
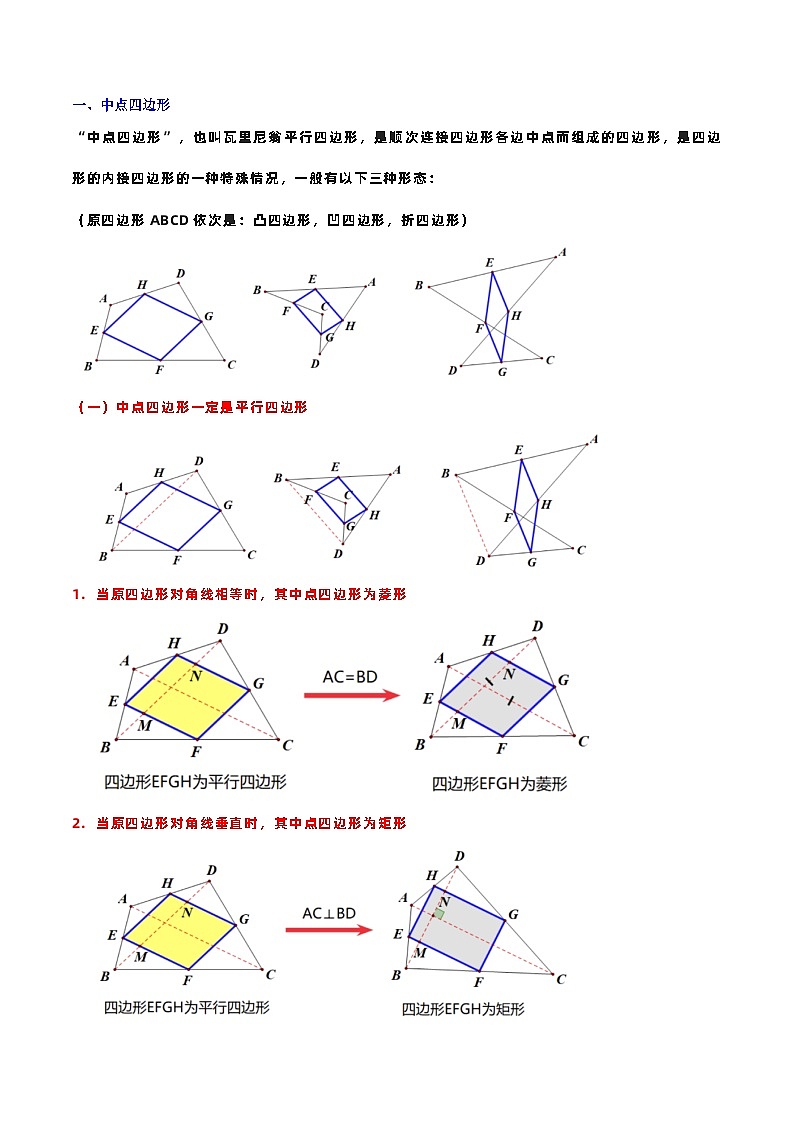
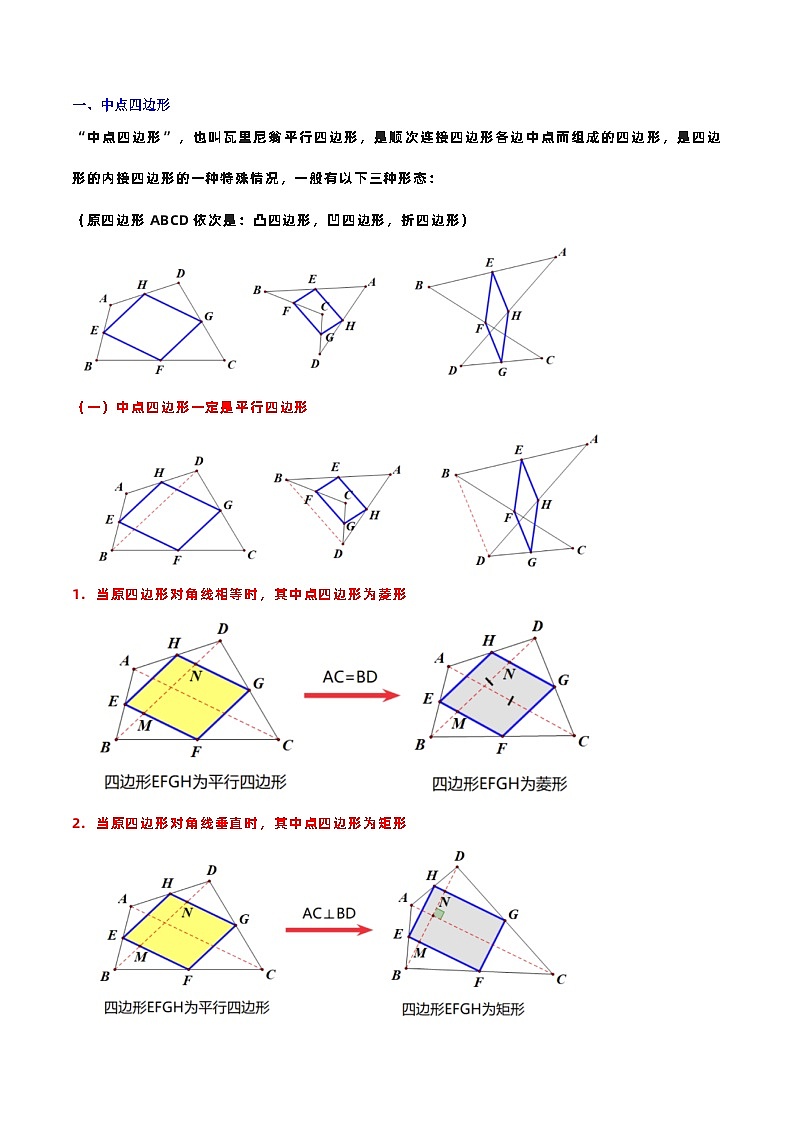
“中点四边形”，也叫瓦里尼翁平行四边形，是顺次连接四边形各边中点而组成的四边形，是四边形的内接四边形的一种特殊情况，一般有以下三种形态：
（原四边形ABCD依次是：凸四边形，凹四边形，折四边形）
（一）中点四边形一定是平行四边形
当原四边形对角线相等时，其中点四边形为菱形
当原四边形对角线垂直时，其中点四边形为矩形
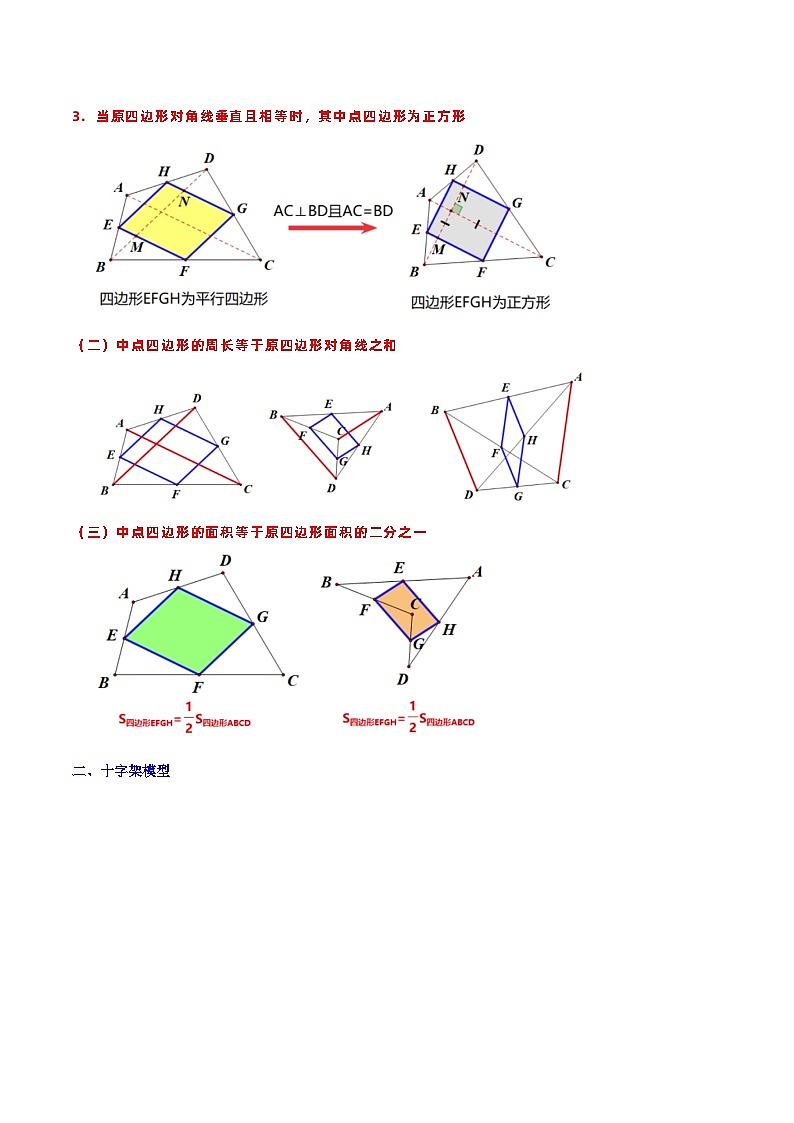
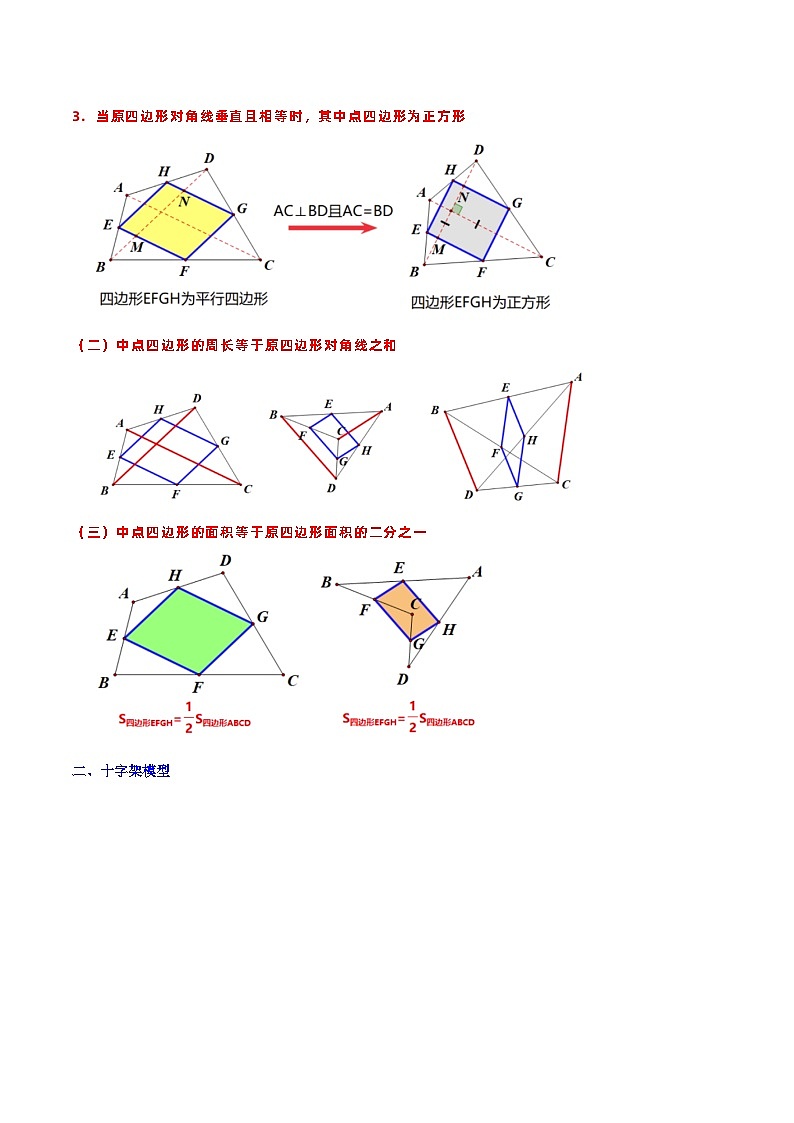
当原四边形对角线垂直且相等时，其中点四边形为正方形
（二）中点四边形的周长等于原四边形对角线之和
（三）中点四边形的面积等于原四边形面积的二分之一
二、十字架模型
三、梯子模型
梯子问题果非常重要的一类最值问题，关键点在于取梯子的中点运用斜边中线和勾股定理来解决，得到两条线段的和是所求的最大值.
例题：如图所示，一根长2.5米的木棍AB斜靠在与地面垂直的墙上,此时墙角0与木棍B端的距离为1.5米,设木棍的中点为P,若木棍A端沿墙下滑,则B端沿地面向右滑行.
(1)木棍在滑动过程中,线段OP的长度发生改变了吗?请说明理由;若不变,求OP的长.
梯子下滑的过程中P离墙角的距离都是一样的.
(2)如果木棍的底端B向外滑出0.9米,那么木棍的顶端A沿墙下滑多少米?
梯子下滑的过程中P离墙角的距离都是一样的.
取公共边中点是关键，辅助线添加构造模型
直角三角形斜边上的中线等于斜边的一半
四、对角互补模型
模型1:全等形一-90°对角互补模型
模型2:全等形--120°对角互补模型
模型 3:全等形一一任意角对角互补模型
模型4:相似形一-90°对角互补模型（后面会学到）
五、与正方形有关三垂线

六、正方形与45°角的基本图

能力拓展
题型一：中点四边形
一、单选题
1．（2022春·贵州遵义·八年级校考期中）我们把顺次连接任意一个四边形各边中点所得的四边形叫做中点四边形，下列说法正确的是
A．任意一个四边形的中点四边形是菱形
B．任意一个平行四边形的中点四边形是平行四边形
C．对角线相等的四边形的中点四边形是矩形
D．对角线垂直的四边形的中点四边形是正方形
二、填空题
2．（2021春·广西来宾·八年级统考期中）依序连接菱形各边中点所得的四边形是___________（指特殊四边形）．
3．（2021春·新疆省直辖县级单位·八年级统考期末）顺次连结对角线相等且垂直的四边形各边中点所得的四边形是___________．
4．（2022春·上海闵行·八年级上海市民办文绮中学校考阶段练习）若顺次连接四边形ABCD四边中点所得的四边形是菱形，则原四边形的对角线AC、BD所满足的条件是________．
5．（2020春·江苏常州·八年级统考期末）若顺次连接四边形ABCD四边中点形成的四边形为矩形，则四边形ABCD满足的条件为.___________
三、解答题
6．（2021春·江苏泰州·八年级高港实验学校校考阶段练习）如图1，在四边形中，如果对角线和相交并且相等，那么我们把这样的四边形称为等角线四边形．
（1）①在“平行四边形、矩形、菱形”中，______一定是等角线四边形（填写图形名称）；
②若、、、分别是等角线四边形四边、、、的中点，当对角线、还要满足______时，四边形是正方形．
（2）如图2，已知在中，，，，为平面内一点．
①若四边形是等角线四边形，且，求符合条件的等角线四边形的面积．
②设点是所在平面上的任意一点且，若四边形是等角线四边形，求出四边形面积的最大值，并说明理由．
7．（2021春·广西桂林·八年级统考期末）如图，四边形ABCD的四边中点分别为E、F、G、H，顺次连接E、F、G、H．
（1）判断四边形EFGH形状，并说明理由；
（2）若AC＝BD，判断四边形EFGH形状，并说明理由．
8．（2021春·河北石家庄·八年级统考期中）四边形ABCD中，点E、F、G、H分别为AB、BC、CD、DA边的中点，顺次连接各边中点得到的新四边形EFGH称为中点四边形．
（1）我们知道：无论四边形ABCD怎样变化，它的中点四边形EFGH都是平行四边形．特殊的：
①当对角线时，四边形ABCD的中点四边形为__________形；
②当对角线时，四边形ABCD的中点四边形是__________形．
（2）如图：四边形ABCD中，已知，且，请利用（1）中的结论，判断四边形ABCD的中点四边形EFGH的形状并进行证明．
题型二：十字架模型
一、单选题
1．（2022春·江苏无锡·八年级校考期末）如图，将边长为3的正方形ABCD纸片沿EF折叠，点C落在AB边上的点G处，点D与点H重合，CG与EF交于点P，取GH的中点Q，连接PQ，则GPQ的周长最小值是（ ）
A．B．C．D．
2．（2021秋·湖北省直辖县级单位·八年级校考期中）如图，将一边长为12的正方形纸片ABCD的顶点A折叠至DC边上的点E，使DE=5，折痕为PQ，则PQ的长为（ ）
A．12B．13C．14D．15
二、填空题
3．（2020春·湖北武汉·八年级校考阶段练习）如图，将边长为8的正方形纸片ABCD折叠，使点D落在BC边的点E处，点A落在点F处，折痕为MN，若MN＝4，则线段CN的长是____．
4．（2021·全国·八年级专题练习）如图，在正方形ABCD中，点E是BC上一点，BF⊥AE交DC于点F，若AB＝5，BE＝2，则AF＝____．
三、解答题
5．（2021春·云南曲靖·八年级统考期末）如图1，在正方形中，为上一点，连接，过点作于点，交于点．
（1）求证：；
（2）如图2，连接、，点、、、分别是、、、的中点，试判断四边形的形状，并说明理由；
（3）如图3，点、分别在正方形的边、上，把正方形沿直线翻折，使得的对应边恰好经过点，过点作于点，若，正方形的边长为3，求线段的长．
6．（2021春·江苏泰州·八年级统考期末）如图，正方形ABCD边长为4，点G在边AD上（不与点A、D重合），BG的垂直平分线分别交AB、CD于E、F两点，连接EG．
（1）当AG=1时，求EG的长；
（2）当AG的值等于 时，BE=8－2DF；
（3）过G点作GM⊥EG交CD于M
①求证：GB平分∠AGM；
②设AG=x，CM=y，试说明的值为定值．
题型三：梯子模型
一、填空题
1．（2021·全国·八年级专题练习）如图，在Rt△ABC中，∠BAC＝90°，AB＝1，AC＝4，点A在y轴上，点C在x轴上，则点A在移动过程中，BO的最大值是_____．
二、解答题
2．（2022秋·江苏南京·八年级南京市竹山中学校考阶段练习）如图，一架云梯AB长25m，斜靠在一面墙上，梯子靠墙的一端A距地面24m．
（1）这个梯子底端B离墙有多少米？
（2）如果梯子的顶端下滑的距离AD＝4m，求梯子的底部B在水平方向滑动的距离BE的长．
3．（2022秋·江苏·八年级专题练习）如图，一架25米长的梯子斜靠在一竖直的墙上，梯子底端离墙有7米．
（1）求梯子靠墙的顶端距地面有多少米？
（2）小燕说“如果梯子的顶端沿墙下滑了4米，那么梯子的底端在水平方向就滑动了4米．”她的说法正确吗？若不正确，请说明理由．
4．（2022秋·全国·八年级专题练习）如图，一个梯子斜靠在一面墙上，梯子底端为，梯子的顶端距地面的垂直距离为的长．
（1）若梯子的长度是，梯子的顶端距地面的垂直距离为．如果梯子的顶端下滑，那么梯子的底端向外滑动多少米?
（2）设，，，且，请思考，梯子在滑动的过程中，是否一定存在顶端下滑的距离与底端向外滑动的距离相等的情况?若存在，请求出这个距离；若不存在，说明理由．
5．（2021·江苏徐州·统考一模）如图，梯子斜靠在与地面垂直（垂足为O）的墙上．当梯子位于AB位置时，它与地面所成的角∠ABO＝60°，当梯子底端向右滑动0.5m（即BD＝0.5m）到达CD位置时，它与地面所成的角∠CDO＝51°18′，求梯子的长．（参考数据：sin51°18′＝0.780，cs51°18′＝0.625，tan51°18′＝1.248）
6．（2023春·全国·八年级专题练习）如图所示，一架梯子AB斜靠在墙面上，且AB的长为2.5米．
（1）若梯子底端离墙角的距离OB为1.5米，求这个梯子的顶端A距地面有多高？
（2）在（1）的条件下，如果梯子的顶端A下滑0.5米到点A'，那么梯子的底端B在水平方向滑动的距离BB'为多少米？
题型四：对角互补模型
一、单选题
1．（2021·全国·八年级专题练习）如图，为等边三角形，以为边向外作，使，再以点C为旋转中心把旋转到，则给出下列结论：①D，A，E三点共线；②平分；③；④．其中正确的有（ ）．
A．1个B．2个C．3个D．4个
二、填空题
2．（2022秋·江苏·八年级专题练习）如图，在Rt△ABC和Rt△BCD中，∠BAC＝∠BDC＝90°，BC＝8，AB＝AC，∠CBD＝30°，BD＝4，M，N分别在BD，CD上，∠MAN＝45°，则△DMN的周长为_____．
3．（2019春·江苏南京·八年级校联考期末）如图，在平面直角坐标系xOy中，A,B两点分别在x轴，y轴的正半轴上，且OA=OB，点C在第一象限，OC=3，连接BC，AC，若∠BCA=90°，则BC+AC的值为_________．
三、解答题
4．（2022秋·山西吕梁·八年级统考期末）（1）如图①，在四边形中，，，，分别是边，上的点，且．请直接写出线段，，之间的数量关系：__________；
（2）如图②，在四边形中，，，，分别是边，上的点，且，（1）中的结论是否仍然成立？请写出证明过程；
（3）在四边形中，，，，分别是边，所在直线上的点，且．请画出图形（除图②外），并直接写出线段，，之间的数量关系．
5．（2022秋·八年级课时练习）四边形是由等边和顶角为的等腰排成，将一个角顶点放在处，将角绕点旋转，该交两边分别交直线、于、，交直线于、两点．
（1）当、都在线段上时（如图1），请证明：；
（2）当点在边的延长线上时（如图2），请你写出线段，和之间的数量关系，并证明你的结论；
（3）在（1）的条件下，若，，请直接写出的长为 ．
6．（2021秋·陕西西安·八年级交大附中分校校考开学考试）问题探究
（（1）如图①，已知∠A=45°，∠ABC=30°，∠ADC=40°，则∠BCD的大小为___________；
（2）如图②，在四边形ABCD中，AB=BC，∠ABC=∠ADC=90°，对角线BD=6．求四边形ABCD的面积；小明这样来计算．延长DC，使得CE=AD，连接BE，通过证明△ABD≌△CBE，从而可以计算四边形ABCD的面积．请你将小明的方法完善．并计算四边形ABCD的面积；
问题解决
（3）如图③，四边形ABCD是正在建设的城市花园，其中AB=BC，∠ABC=60°，∠ADC=30°，DC=40米，AD=30米．请计算出对角线BD的长度．
7．（2021春·福建三明·八年级统考期中）感知：如图①，平分，，．判断与的大小关系并证明．
探究：如图②，平分，，，与的大小关系变吗？请说明理由．
应用：如图③，四边形中，，，，则与差是多少（用含的代数式表示）
8．（2020春·江西萍乡·八年级统考期末）【课题研究】旋转图形中对应线段所在直线的夹角（小于等于90°的角）与旋转角的关系．
【问题初探】线段AB绕点O顺时针旋转得到线段CD，其中点A与点C对应，点B与点D对应，旋转角的度数为α，且0°＜α＜180°．
（1）如图①，当α＝60°时，线段AB、CD所在直线夹角（锐角）为 ；
（2）如图②，当90°＜α＜180°时，直线AB与直线CD所夹锐角与旋转角α存在怎样的数量关系？请说明理由；
【形成结论】旋转图形中，当旋转角小于平角时，对应线段所在直线的夹角与旋转角 ．
【运用拓广】运用所形成的结论解决问题：
（3）如图③，四边形ABCD中，∠ABC＝60°，∠ADC＝30°，AB＝BC，CD＝3，BD＝，求AD的长．
9．（2021·全国·八年级专题练习）我们规定：一组邻边相等且对角互补的四边形叫作“完美四边形”．
（1）在①平行四边形，②菱形，③矩形，④正方形中，一定为“完美”四边形的是 （请填序号）；
（2）在“完美”四边形ABCD中，AB=AD，∠B+∠D=180°，连接AC．
①如图1，求证：AC平分∠BCD；
小明通过观察、实验，提出以下两种想法，证明AC平分∠BCD：
想法一：通过∠B+∠D=180°，可延长CB到E，使BE=CD，通过证明△AEB≌△ACD，从而可证AC平分∠BCD；
想法二：通过AB=AD，可将△ACD绕点A顺时针旋转，使AD与AB重合，得到△AEB，可证C,B,E三点在条直线上，从而可证AC平分∠BCD．
请你参考上面的想法，帮助小明证明AC平分∠BCD；
②如图2，当∠BAD=90°，用等式表示线段AC,BC,CD之间的数量关系，并证明.

题型五：与正方形有关三垂线
一、单选题
1．（2022秋·江苏·八年级专题练习）如图，四边形AFDC是正方形，和都是直角，且E，A，B三点共线，，则图中阴影部分的面积是（ ）
A．12B．10C．8D．6
二、填空题
2．（2023春·八年级课时练习）如图所示，直线a经过正方形ABCD的顶点A，分别过正方形的顶点B、D作BF⊥a于点F，DE⊥a于点E，若DE＝8，BF＝5，则EF的长为__．
三、解答题
3．（2022春·广东东莞·八年级塘厦初中校考期中）四边形ABCD为正方形，点E为线段AC上一点，连接DE，过点E作EF⊥DE，交射线BC于点F，以DE、EF为邻边作矩形DEFG，连接CG．
（1）如图，求证：矩形DEFG是正方形；
（2）若AB＝4，CE＝2，求CG的长度；
（3）当线段DE与正方形ABCD的某条边的夹角是40°时，直接写出∠EFC的度数．
4．（2021春·全国·八年级专题练习）如图，在正方形ABCD中，点E，F分别在边AB，BC上，AF与DE相交于点M，且∠BAF＝∠ADE．
（1）如图1，求证：AF⊥DE；
（2）如图2，AC与BD相交于点O，AC交DE于点G，BD交AF于点H，连接GH，试探究直线GH与AB的位置关系，并说明理由；
（3）在（1）（2）的基础上，若AF平分∠BAC，且BDE的面积为4+2，求正方形ABCD的面积．
5．（2021春·安徽安庆·八年级统考期末）如图1，点E为正方形ABCD内一点，∠AEB＝90°，将Rt△ABE绕点B按顺时针方向旋转90°（即∠EBE'＝90°），得到△CBE′（点A的对应点为点C）延长AE交CE于点F，连接DE．
（1）试判断四边形BE′FE的形状，并说明理由．
（2）如图2，若DA＝DE，请猜想线段CF于FE'的数量关系并加以证明．
（3）如图1，若AB＝，CF＝3，请直接写出DE的长．
6．（2021春·山西·八年级统考期末）综合与实践：如图1，在正方形中，连接对角线，点O是的中点，点E是线段上任意一点（不与点A，O重合），连接，．过点E作交直线于点F．
（1）试猜想线段与的数量关系，并说明理由；
（2）试猜想线段之间的数量关系，并说明理由；
（3）如图2，当E在线段上时（不与点C，O重合），交延长线于点F，保持其余条件不变，直接写出线段之间的数量关系．
7．（2021春·全国·八年级专题练习）四边形是边长为的正方形，点在边所在的直线上，连接，以为直角顶点在右侧作等腰，连接

（1）如图1，当点在点左侧，且三点共线时，______；
（2）如图2，当点在点右侧，且时，求的长：
（3）若点在边所在直线上，且，求的长．
8．（2022春·新疆省直辖县级单位·八年级校联考期末）如图，点是正方形的边上的任意一点（不与、重合），与正方形的外角的角平分线交于点．
(1)求证：．
(2)将图放在平面直角坐标系中，如图，连、，与交于点，若正方形的边长为，则四边形的面积是否随点位置的变化而变化？若不变，请求出四边形的面积．
(3)在的（2）条件下，若，求四边形的面积．
9．（2021春·全国·八年级专题练习）如图①，已知△ABC是等腰直角三角形，∠BAC＝90°，点D是BC的中点．作正方形DEFG，使点A、C分别在DG和DE上，连接AE，BG．
（1）试猜想线段BG和AE的关系（直接写出答案，不用证明）；
（2）将正方形DEFG绕点D逆时针方向旋转α （0°＜α≤60°），判断（1）中的结论是否仍然成立？请利用图②证明你的结论；
（3）若BC＝DE＝4，当α等于多少度时，AE最大？并求出此时AF的值．
六、正方形与45°角的基本图
一、填空题
1．（2021春·江苏南京·八年级校考期中）如图，在正方形ABCD中，点M、N为边BC和CD上的动点（不含端点），，下列三个结论：①当MN＝MC时，则；②2；③△MNC的周长不变；④∠AMN－∠AMB＝60°．其中正确结论的序号是________．
二、解答题
2．（2023春·江苏·八年级专题练习）如图所示，正方形中，点E，F分别为BC，CD上一点，点M为EF上一点，，M关于直线AF对称．
（1）求证：B，M关于AE对称；
（2）若的平分线交AE的延长线于G，求证：．
3．（2023春·江苏·八年级专题练习）（1）如图①，在正方形中，、分别是、上的点，且，连接，探究、、之间的数量关系，并说明理由；
（2）如图②，在四边形中，，，、分别是、上的点，且，此时（1）中的结论是否仍然成立？请说明理由．
4．（2023春·江苏·八年级专题练习）如图所示，正方形中，点E，F分别为BC，CD上一点，点M为EF上一点，D，M关于直线AF对称．连结DM并延长交AE的延长线于N，求证：．
5．（2023春·江苏·八年级专题练习）如图1，在正方形中，E是上一点，F是延长线上一点，且．
（1）求证：；
（2）在图1中，若G在上，且，则成立吗？为什么？
（3）运用（1）（2）解答中所积累的经验和知识，完成下题：
①如图2，在直角梯形中，，，，E是上一点，且，，求的长．
②如图3，在中，，，，，则的面积为____（直接写出结果，不需要写出计算过程）
6．（2023春·江苏·八年级专题练习）如图正方形的边、在坐标轴上，已知点．将正方形绕点顺时针旋转一定的角度（小于），得到正方形，交线段于点，的延长线交线段于点，连接、．
（1）求的度数．
（2）当时，求点的坐标．
（3）在（2）的条件下，直线上是否存在点，使以、、为顶点的三角形是等腰三角形？若存在，请直接写出点的坐标，若不存在，请说明理由．
7．（2023春·江苏·八年级专题练习）已知正方形，，绕点A顺时针旋转，它的两边分别交、于点M、N，于点H．
（1）如图①，当时，可以通过证明，得到与的数量关系，这个数量关系是___________；
（2）如图②，当时，（1）中发现的与的数量关系还成立吗？说明理由；
（3）如图③，已知中，，于点H，，，求的长．
8．（2023春·江苏·八年级专题练习）已知四边形ABCD是正方形，一个等腰直角三角板的一个锐角顶点与A点重合，将此三角板绕A点旋转时，两边分别交直线BC，CD于M，N．
(1)如图1，当M，N分别在边BC，CD上时，求证：BM+DN=MN
(2)如图2，当M，N分别在边BC，CD的延长线上时，请直接写出线段BM，DN，MN之间的数量关系
(3)如图3，直线AN与BC交于P点，MN=10，CN=6，MC=8，求CP的长．
9．（2021春·江苏扬州·八年级统考期末）【问题情境】
在综合实践课上，同学们以“正方形和直线的旋转”为主题分组开展数学探究活动，已知正方形，直线经过点，并绕点旋转，作点关于直线的对称点，直线交直线于点，连结、．
【操作发现】
（1）如图1，若．则 °， °．
【拓展应用】
（2）如图2，当直线在正方形的外部时
①判断的度数是否为一个定值？如果是，请求出此定值；如果不是，请说明理由．
②线段、、之间存在特殊的数量关系，请写出这一关系式，并说明理由．
10．（2023春·江苏·八年级专题练习）已知：四边形为正方形，是等腰，．
（1）如图：当绕点旋转时，若边、分别与、相交于点、，连接，试证明：．
（2）如图，当绕点旋转时，若边、分别与、的延长线相交于点、，连接．
①试写出此时三线段、、的数量关系并加以证明．
②若，，求：正方形的边长以及中边上的高．
11．（2023春·江苏·八年级专题练习）已知正方形ABCD，∠EAF＝45°，将∠EAF绕顶点A旋转，角的两边始终与直线CD交于点E，与直线BC交于点F，连接EF．
（1）如图①，当BF＝DE时，求证：△ABF≌△ADE；
（2）若∠EAF旋转到如图②的位置时，求证：∠AFB＝∠AFE；
（3）若BC＝4，当边AE经过线段BC的中点时，在AF的右侧作以AF为腰的等腰直角三角形AFP，直接写出点P到直线AB的距离．