江苏八年级下期末真题精选（压轴60题19个考点专练）-【满分全攻略】2022-2023学年八年级数学下学期核心考点+重难点讲练与测试（苏科版）

这是一份江苏八年级下期末真题精选（压轴60题19个考点专练）-【满分全攻略】2022-2023学年八年级数学下学期核心考点+重难点讲练与测试（苏科版），文件包含江苏八年级下期末真题精选压轴60题19个考点专练原卷版docx、江苏八年级下期末真题精选压轴60题19个考点专练解析版docx等2份试卷配套教学资源，其中试卷共113页， 欢迎下载使用。

1．（2022秋•市中区期末）观察下列各式：
＝1+﹣＝1
＝1+﹣＝1
＝1+﹣＝1
请你根据上面三个等式提供的信息，猜想：
（1）＝ 1
（2）请你按照上面每个等式反映的规律，写出用n（n为正整数）表示的等式： ＝1+ ；
（3）利用上述规律计算：（仿照上式写出过程）
【分析】（1）根据提供的信息，即可解答；
（2）根据规律，写出等式；
（3）根据（2）的规律，即可解答．
【解答】解：（1）＝1＝1；故答案为：1；
（2）＝1+＝1+；故答案为：＝1+；
（3）．
【点评】本题考查了二次根式的性质与化简，解决本题的关键是关键信息，找到规律．
二．分式方程的应用（共1小题）
2．（2016•哈尔滨）早晨，小明步行到离家900米的学校去上学，到学校时发现眼镜忘在家中，于是他立即按原路步行回家，拿到眼镜后立即按原路骑自行车返回学校．已知小明步行从学校到家所用的时间比他骑自行车从家到学校所用的时间多10分钟，小明骑自行车速度是步行速度的3倍．
（1）求小明步行速度（单位：米/分）是多少；
（2）下午放学后，小明骑自行车回到家，然后步行去图书馆，如果小明骑自行车和步行的速度不变，小明步行从家到图书馆的时间不超过骑自行车从学校到家时间的2倍，那么小明家与图书馆之间的路程最多是多少米？
【分析】（1）设小明步行的速度是x米/分，根据题意可得等量关系：小明步行回家的时间＝骑车返回时间+10分钟，根据等量关系列出方程即可；
（2）根据（1）中计算的速度列出不等式解答即可．
【解答】解：（1）设小明步行的速度是x米/分，由题意得：
，
解得：x＝60，
经检验：x＝60是原分式方程的解，
答：小明步行的速度是60米/分；
（2）设小明家与图书馆之间的路程是y米，根据题意可得：
，
解得：y≤600，
答：小明家与图书馆之间的路程最多是600米．
【点评】此题主要考查了分式方程的应用，关键是正确理解题意，找出题目中的等量关系，列出方程．
三．反比例函数系数k的几何意义（共7小题）
3．（2022春•邗江区期末）如图，△AOB和△ACD均为正三角形，且顶点B、D均在双曲线（x＞0）上，连接BC交AD于P，连接OP，则图中S△OBP是（ ）
A．B．3C．6D．12
【分析】先根据△AOB和△ACD均为正三角形可知∠AOB＝∠CAD＝60°，故可得出AD∥OB，所以S△ABP＝S△AOP，故S△OBP＝S△AOB，过点B作BE⊥OA于点E，由反比例函数系数k的几何意义即可得出结论．
【解答】解：如图：
∵△AOB和△ACD均为正三角形，
∴∠AOB＝∠CAD＝60°，
∴AD∥OB，
∴S△ABP＝S△AOP，
∴S△OBP＝S△AOB，
过点B作BE⊥OA于点E，则S△OBE＝S△ABE＝S△AOB，
∵点B在反比例函数y＝的图象上，
∴S△OBE＝×6＝3，
∴S△OBP＝S△AOB＝2S△OBE＝6．
故选：C．
【点评】本题考查的是反比例函数综合题，涉及到等边三角形的性质及反比例函数系数k的几何意义等知识，难度适中．
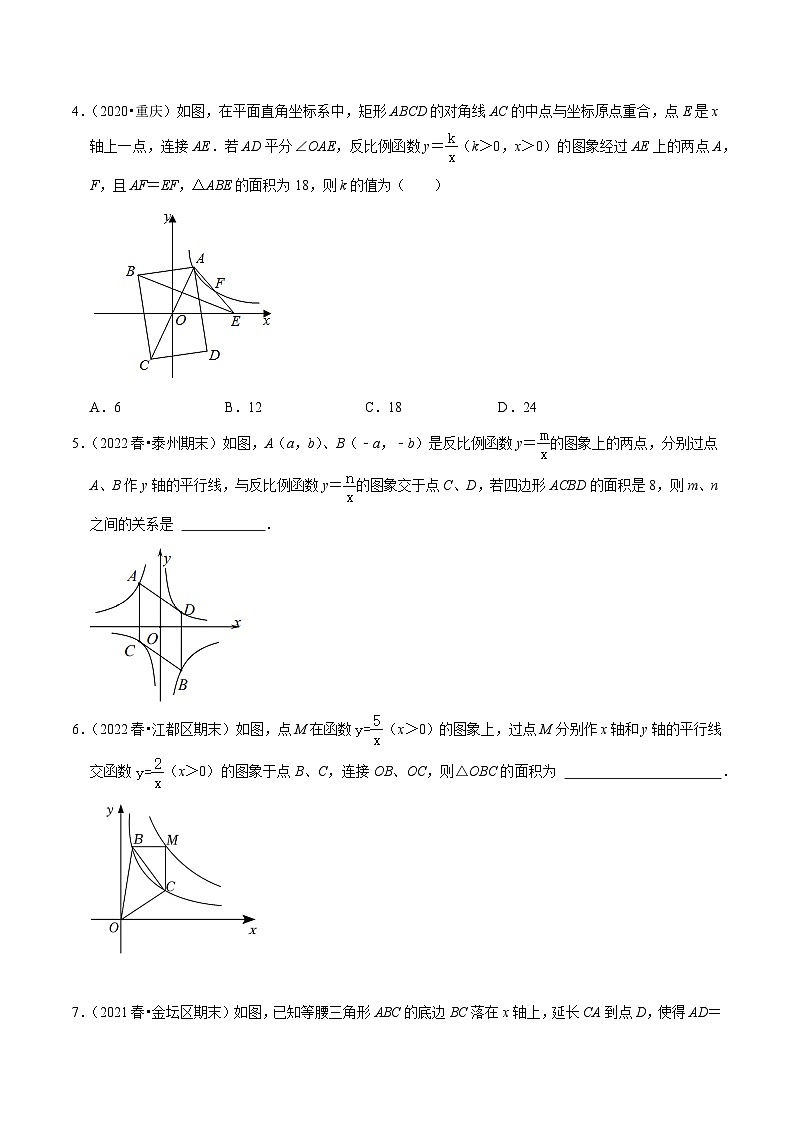
4．（2020•重庆）如图，在平面直角坐标系中，矩形ABCD的对角线AC的中点与坐标原点重合，点E是x轴上一点，连接AE．若AD平分∠OAE，反比例函数y＝（k＞0，x＞0）的图象经过AE上的两点A，F，且AF＝EF，△ABE的面积为18，则k的值为（ ）
A．6B．12C．18D．24
【分析】如图，连接BD，OF，过点A作AN⊥OE于N，过点F作FM⊥OE于M．证明BD∥AE，推出S△ABE＝S△AOE＝18，推出S△EOF＝S△AOE＝9，可得S△FME＝S△EOF＝3，由此即可解决问题．
【解答】解：如图，连接BD，OF，过点A作AN⊥OE于N，过点F作FM⊥OE于M．
∵AN∥FM，AF＝FE，
∴MN＝ME，
∴FM＝AN，
∵A，F在反比例函数的图象上，
∴S△AON＝S△FOM＝，
∴•ON•AN＝•OM•FM，
∴ON＝OM，
∴ON＝MN＝EM，
∴ME＝OE，
∴S△FME＝S△FOE，
∵AD平分∠OAE，
∴∠OAD＝∠EAD，
∵四边形ABCD是矩形，
∴OA＝OD，
∴∠OAD＝∠ODA＝∠DAE，
∴AE∥BD，
∴S△ABE＝S△AOE，
∴S△AOE＝18，
∵AF＝EF，
∴S△EOF＝S△AOE＝9，
∴S△FME＝S△EOF＝3，
∴S△FOM＝S△FOE﹣S△FME＝9﹣3＝6＝，
∴k＝12．
故选：B．
【点评】本题考查反比例函数的性质，矩形的性质，平行线的判断和性质，等高模型等知识，解题的关键是证明BD∥AE，利用等高模型解决问题，属于中考选择题中的压轴题．
5．（2022春•泰州期末）如图，A（a，b）、B（﹣a，﹣b）是反比例函数y＝的图象上的两点，分别过点A、B作y轴的平行线，与反比例函数y＝的图象交于点C、D，若四边形ACBD的面积是8，则m、n之间的关系是 n﹣m＝4 ．
【分析】连接AB，OC，根据反比例函数的性质可得点O在线段AB上，且OA＝OB，由点A（a，b）是反比例函数y＝的图象上的点，可得b＝，由AC∥y轴，可得点C的坐标为（a，），进而可得AC＝BD的长，从而可以判断四边形ACBD是平行四边形，根据平行四边形的性质可得S△AOC＝S△ACB＝S平行四边形ACBD＝2，然后根据三角形的面积公式可得AC|a|＝2，整理得：n﹣m＝4．
【解答】解：连接AB，OC，如图，
∵A（a，b）、B（﹣a，﹣b）关于原点对称，且是反比例函数y＝的图象上的两点，
∴点O在线段AB上，且OA＝OB，
∵A（a，b）是反比例函数y＝的图象上的点，
∴b＝，
∵AC∥y轴，
∴点C的坐标为（a，），
∴AC＝|﹣|，
同理可得BD＝|﹣|，
∴AC＝BD，
∴四边形ACBD是平行四边形，
∴S△AOC＝S△ACB＝S平行四边形ACBD＝2，
∴AC|a|＝2，
∴（﹣）•（﹣a）＝2，
整理得：n﹣m＝4．
故答案为：n﹣m＝4．
【点评】本题考查了反比例函数系数k的几何意义、反比例函数图象上点的坐标特征、平行四边形的判定与性质、三角形面积等知识，属于常考题型，熟练掌握反比例函数的图象和性质是解题关键．
6．（2022春•江都区期末）如图，点M在函数（x＞0）的图象上，过点M分别作x轴和y轴的平行线交函数（x＞0）的图象于点B、C，连接OB、OC，则△OBC的面积为 ． ．
【分析】设M（m，），可得C（m，），B（，），由三角形的面积公式S△OBC＝S矩形ODME﹣S△OCE﹣S△ODB﹣S△MBC可求解．
【解答】解：延长MB交y轴于点D，延长MC交x轴于点E，
设M（m，），可得C（m，），B（，），
∴D（0，），E（m，0），
∴S△OBC＝S矩形ODME﹣S△OCE﹣S△ODB﹣S△MBC
＝5﹣﹣﹣﹣
＝5﹣1﹣1﹣
＝．
故答案为：．
【点评】主要考查了反比例函数图象上各个点的坐标之间的关系，设出点M的坐标，从而得出点B和C的坐标是解决问题的关键．
7．（2021春•金坛区期末）如图，已知等腰三角形ABC的底边BC落在x轴上，延长CA到点D，使得AD＝AC，延长AB交y轴于点E，连接CE，点D落在反比例函数y＝（k≠0）的图象上．若△BCE的面积等于2，则k＝ 4 ．
【分析】连接CD，ED，BD，通过AD＝AC，AB＝AC推导出S△BED＝S△BEC＝2及DB⊥x轴，再由DB平行于y轴可得＝S△DBO＝S△DBE＝2，进而求解．
【解答】解：连接CD，ED，BD，
∵AD＝AC，
∴S△ABD＝S△ABC，S△EAD＝S△EAC，
∴S△BED＝S△BEC＝2，
∵AB＝AC，AD＝AC，
∴AD＝AB，
∴∠ABC＝∠ACB，∠ADB＝∠ABD，
∵∠ABC+∠ACB+∠ADB+∠ABD＝180°，
∴∠ABD+∠ABC＝（∠ABC+∠ACB+∠ADB+∠ABD）＝90°，
∴DB⊥OC，
∵OE∥DB，
∴＝S△DBO＝S△DBE＝2，
∴k＝4．
故答案为：4．
【点评】本题考查反比例函数与图形的结合，解题关键是熟练掌握反比例函数系数k的几何意义，通过添加辅助线求解．
8．（2022春•高邮市期末）如图，在平面直角坐标系中，△ABO的边AB平行于y轴，反比例函数的图象经过OA的中点C和点B，若△OAB的面积为6，则k＝ ﹣4 ．
【分析】延长AB交x轴于D，根据反比例函数y＝（x＞0）的图象经过点B，设B（x，），则OD＝x，根据△OAB的面积为9，列等式可表示AB的长，表示点A的坐标，根据线段中点坐标公式可得C的坐标，从而得出结论．
【解答】解：如图，延长AB交x轴于D，
∵AB∥y轴，
∴AD⊥x轴，
∵反比例函数y＝（x＜0）的图象经过OA中点C和点B，
∴设B（x，），则OD＝﹣x，
∵△OAB的面积为6，
∴AB•OD＝6，
∴AB•（﹣x）＝6，
∴AB＝﹣，
∴A（x，﹣），
∵C是OA的中点，
∴C（，﹣），
∴k＝•（﹣），
∴k＝﹣4．
故答案为：﹣4．
【点评】此题主要考查了反比例函数上点的坐标特征，线段的中点坐标公式，三角形面积公式，解本题的关键是设未知数建立方程解决问题．
9．如图，在平面直角坐标系中，C，A分别为x轴、y轴正半轴上的点，以OA，OC为边，在第一象限内作矩形OABC，且S矩形OABC＝2，将矩形OABC翻折，使点B与原点O重合，折痕为MN，点C的对应点C′落在第四象限，过M点的反比例函数y＝（k≠0）的图象恰好过MN的中点，点C′的坐标为 （，﹣） ．
【分析】利用△BQM≌△OQN（AAS），得到点Q是MN的中点，利用Rt△OHQ∽Rt△OCB得到＝＝，求出k的值，设AM＝a，则BM＝3a＝OM，求得OA＝2a，再根据反比例函数系数k的几何意义求得a，从而求得OC′＝BC＝OA＝2，ON＝BN＝OM＝，根据三角形面积求得C′G，再根据勾股定理即可求得OG，从而求得C′的坐标．
【解答】解：如图，连接OB，交MN于点Q，
∵矩形OABC翻折，使点B与原点重合，折痕为MN，
∴QB＝QO，MB＝MO，
∵AB∥CO，
∴∠ABQ＝∠NOQ，
∵∠MQB＝∠NQO，
而OQ＝BQ，
∴△BQM≌△OQN（AAS），
∴QM＝QN，即点Q是MN的中点，
过点Q作QH⊥BC于点H，则QH是△OBC的中位线，
则Rt△OHQ∽Rt△OCB，
则＝＝，
而S△OBC＝S矩形AOCB＝，
则S△OHQ＝×＝k，
解得k＝，
∵点M是反比例函数上的点，
则S△AOM＝k＝，
而S△ABO＝S矩形AOCB＝＝4S△AOM，
故AM＝AB，
设AM＝a，则BM＝3a＝OM，
则OA＝2a，
则S△AOM＝＝AM•AO＝a•2a，
解得a＝（负值已舍去），
则AB＝4AM＝2，AM＝a＝，
连接BN，作C′G⊥ON于G，
∵QO＝BQ，QM＝NQ，
∴四边形MONB是平行四边形，
∴ON＝BN＝OM，
∵OC′＝BC＝OA，
∴Rt△AOM≌Rt△CBN≌Rt△C′ON（HL），
∴S△C′ON＝S△AOM＝，ON＝OM＝，OC′＝OA＝2＝，
∴ON•C′G＝，
∴×C′G＝，
∴C′G＝，
∴OG＝，
∴C′为（，﹣），
故答案为：（，﹣）．
【点评】此题考查了翻折变换，反比例函数系数k的几何意义，反比例函数图象上点的坐标特征，三角形全等的判定与性质，坐标与图形变换﹣对称，矩形的性质，面积的计算以及勾股定理等，解决本题的关键是综合运用以上知识，难度较大．
四．反比例函数图象上点的坐标特征（共1小题）
10．（2021春•罗湖区校级期末）如图，以矩形OABC的顶点O为坐标原点建立平面直角坐标系，使点A、C分别在x轴、y轴的正半轴上，双曲线y＝（x＞0）的图象经过BC的中点D，且与AB交于点E．过OC边上一点F，把△BCF沿直线BF翻折，使点C落在点C′处（点C′在矩形OABC内部），且C′E∥BC，若点C′的坐标为（2，3），则k的值为（ ）
A．B．C．D．
【分析】首先证明点E是线段AB的中点，设BC＝BC′＝m，则EC′＝m﹣2．在Rt△BEC′中，根据BC′2＝BE2+EC′2，构建方程求出m即可解决问题；
【解答】解：连接OD、OE．设BC＝BC′＝m，则EC′＝m﹣2．
∵CD＝BD，
∴S△CDO＝＝S矩形ABCD，
∵S△AOE＝＝S△CDO＝S矩形ABCD，
∴AE＝EB，
∵C′（2，3），
∴AE＝EB＝3，
在Rt△BEC′中，∵BC′2＝BE2+EC′2，
∴m2＝32+（m﹣2）2，
∴m＝，
∴E（，3），
∵点E在y＝上，
∴k＝，
故选：D．
【点评】本题考查了反比例函数综合题，涉及待定系数法求函数解析式、翻折变换、勾股定理等知识，综合性较强，学会利用参数构建方程解决问题．
五．反比例函数与一次函数的交点问题（共6小题）
11．（2021•武威二模）已知反比例函数的图象与一次函数y2＝ax+b的图象交于点A（1，4）和点B（m，﹣2），
（1）求这两个函数的关系式；
（2）观察图象，写出使得y1＞y2成立的自变量x的取值范围．
【分析】（1）将A坐标代入反比例函数解析式中求出k的值，确定出反比例解析式，将B坐标代入反比例解析式中求出m的值，确定出B坐标，将A与B坐标代入一次函数解析式中求出a与b的值，即可确定出一次函数解析式；
（2）利用图象即可得出所求不等式的解集，即为x的范围．
【解答】解：（1）∵函数y1＝的图象过点A（1，4），即4＝，
∴k＝4，
∴反比例函数的关系式为y1＝；
又∵点B（m，﹣2）在y1＝上，
∴m＝﹣2，
∴B（﹣2，﹣2），
又∵一次函数y2＝ax+b过A、B两点，
∴依题意，得，
解得，
∴一次函数的关系式为y2＝2x+2；
（2）根据图象y1＞y2成立的自变量x的取值范围为x＜﹣2或0＜x＜1．
【点评】此题考查了一次函数与反比例函数的交点问题，涉及的知识有：待定系数法求函数解析式，利用了数形结合的思想，熟练运用待定系数法是解本题的关键．
12．（2021春•洪泽区期末）如图，一次函数y＝x﹣7与反比例函数y＝的图象交于A（1，a）和B（b，﹣1）两点．
（1）直接写出a＝ ﹣6 ，b＝ 6 ，k＝ ﹣6 ；
（2）结合图象直接写出关于x的不等式x﹣7＜的解集是 1＜x＜6或x＜0 ；
（3）点C（n，2）在反比例函数y＝的图象上，连接AC、BC，求△ABC的面积．
【分析】（1）用待定系数法即可求解；
（2）观察函数图象即可求解；
（3）由△ABC的面积＝AB×GN，即可求解．
【解答】解：（1）将点A、B的坐标分别代入一次函数表达式得：，解得，
故点A、B的坐标分别为（1，﹣6）、（6，﹣1），
将点A的坐标代入反比例函数表达式得：﹣6＝，解得k＝﹣6，
则反比例函数的表达式为y＝﹣，
故答案为：﹣6，6，﹣6；
（2）从图象看，不等式x﹣7＜的解集是：1＜x＜6或x＜0，
故答案为1＜x＜6或x＜0；
（3）将点C的坐标代入反比例函数表达式得：2＝﹣，解得n＝﹣3，
故点C（﹣3，2），
设直线AB交y轴于点H（0，﹣7），过点C作直线CG∥AB，交y轴于点G，
设直线CG的表达式为y＝x+t，
将点C的坐标代入上式得：2＝﹣3+t，解得t＝5，
故点G（0，5），
则GH＝5+7＝12，
过点G作GN⊥AB于点N，
由直线CG和AB的表达式知，两条直线和x轴坐标轴的夹角为45°，
故GN＝GH＝6，
则△ABC的面积＝AB×GN＝×6＝30．
【点评】本题考查了反比例函数与一次函数的交点，当有两个函数的时候，着重使用一次函数，体现了方程思想，综合性较强．
13．（2022春•安居区期末）如图，在平面直角坐标系中，正比例函数y＝3x与反比例函数y＝的图象交于A，B两点，点A的横坐标为2，AC⊥x轴，垂足为C，连接BC．
（1）求反比例函数的表达式；
（2）求△ABC的面积；
（3）若点P是反比例函数y＝图象上的一点，△OPC与△ABC面积相等，请直接写出点P的坐标．
【分析】（1）把A点横坐标代入正比例函数可求得A点坐标，代入反比例函数解析式可求得k，可求得反比例函数解析式；
（2）根据反比例函数的对称性得出点B的坐标，再利用三角形的面积公式解答即可；
（3）由条件可求得B、C的坐标，可先求得△ABC的面积，再结合△OPC与△ABC的面积相等求得P点坐标．
【解答】解：（1）把x＝2代入y＝3x中，得y＝2×3＝6，
∴点A坐标为（2，6），
∵点A在反比例函数y＝的图象上，
∴k＝2×6＝12，
∴反比例函数的解析式为y＝；
（2）∵AC⊥OC，
∴OC＝2，
∵A、B关于原点对称，
∴B点坐标为（﹣2，﹣6），
∴B到OC的距离为6，
∴S△ABC＝2S△ACO＝2××2×6＝12，
（3）∵S△ABC＝12，
∴S△OPC＝12，
设P点坐标为（x，），则P到OC的距离为||，
∴×||×2＝12，解得x＝1或﹣1，
∴P点坐标为（1，12）或（﹣1，﹣12）．
【点评】本题主要考查待定系数法求函数解析式及函数的交点问题，在（1）中求得A点坐标、在（2）中求得P点到OC的距离是解题的关键．
14．（2018春•宿豫区期末）如图，在平面直角坐标系中，一次函数y＝mx+2（m≠0）的图象与反比例函数y＝（k≠0）的图象交于第一、三象限内的A、B两点，与y轴交于点C，点M在x轴负半轴上，OM＝OC，且四边形OCMB是平行四边形，点A的纵坐标为4．
（1）求该反比例函数和一次函数的表达式；
（2）连接AO，求△AOB的面积；
（3）直接写出关于x的不等式mx＜﹣2的解集．
【分析】（1）先利用一次函数解析式确定C点坐标，再根据平行四边形的性质确定B点坐标，然后利用待定系数法求两个函数解析式；
（2）先确定A点坐标，然后根据三角形面积公式，利用S△AOB＝S△AOC+S△BOC进行计算；
（3）观察函数图象，写出反比例函数图象在一次函数图象上方所对应的自变量的范围即可．
【解答】解：（1）当x＝0时，y＝mx+2＝2，则C（0，2），
∴OM＝OC＝2，
∵四边形OCMB是平行四边形
∴BM∥OC，BM＝OC＝2，
∴B（﹣2，﹣2），
把B（﹣2，﹣2）代入y＝得k＝﹣2×（﹣2）＝4，
∴反比例函数解析式为y＝；
把B（﹣2，﹣2）代入y＝kx+2得﹣2k+2＝﹣2，解得k＝2，
∴一次函数解析式为y＝2x+2；
（2）当y＝4时，2x+2＝4，解得x＝1，则A（1，4），
S△AOB＝S△AOC+S△BOC＝×2×1+×2×2＝3；
（3）当x＜﹣2或0＜x＜1时，mx+2＜，
∴不等式mx＜﹣2的解集为x＜﹣2或0＜x＜1．
【点评】本题考查了反比例函数与一次函数的交点问题：求反比例函数与一次函数的交点坐标，把两个函数关系式联立成方程组求解，若方程组有解则两者有交点，方程组无解，则两者无交点．也考查了待定系数法求函数解析式和平行四边形的性质．
15．（2014•巴中）如图，在平面直角坐标系xOy中，已知四边形DOBC是矩形，且D（0，4），B（6，0）．若反比例函数y＝（x＞0）的图象经过线段OC的中点A，交DC于点E，交BC于点F．设直线EF的解析式为y＝k2x+b．
（1）求反比例函数和直线EF的解析式；
（2）求△OEF的面积；
（3）请结合图象直接写出不等式k2x+b﹣＞0的解集．
【分析】（1）先利用矩形的性质确定C点坐标（6，4），再确定A点坐标为（3，2），则根据反比例函数图象上点的坐标特征得到k1＝6，即反比例函数解析式为y＝；然后利用反比例函数解析式确定F点的坐标为（6，1），E点坐标为（，4），再利用待定系数法求直线EF的解析式；
（2）利用△OEF的面积＝S矩形BCDO﹣S△ODE﹣S△OBF﹣S△CEF进行计算；
（3）观察函数图象得到当＜x＜6时，一次函数图象都在反比例函数图象上方，即k2x+b＞．
【解答】解：（1）∵四边形DOBC是矩形，且D（0，4），B（6，0），
∴C点坐标为（6，4），
∵点A为线段OC的中点，
∴A点坐标为（3，2），
∴k1＝3×2＝6，
∴反比例函数解析式为y＝；
把x＝6代入y＝得y＝1，则F点的坐标为（6，1）；
把y＝4代入y＝得x＝，则E点坐标为（，4），
把F（6，1）、E（，4）代入y＝k2x+b得，解得，
∴直线EF的解析式为y＝﹣x+5；
（2）△OEF的面积＝S矩形BCDO﹣S△ODE﹣S△OBF﹣S△CEF
＝4×6﹣×4×﹣×6×1﹣×（6﹣）×（4﹣1）
＝；
（3）由图象得：不等式k2x+b﹣＞0的解集为＜x＜6．
【点评】本题考查了反比例函数与一次函数的交点问题：求反比例函数与一次函数的交点坐标，把两个函数关系式联立成方程组求解，若方程组有解则两者有交点，方程组无解，则两者无交点．也考查了待定系数法确定函数解析式．
16．（2018春•秦淮区期末）如图，在直角坐标系中，函数y1＝与函数y2＝x的图象交于点A、B．
（1）点A、B的坐标分别是 （2，2） 、 （﹣2，﹣2） ；
（2）在同一平面直角坐标系中，画出函数y3＝﹣的图象；
（3）垂直于y轴的直线l与函数y1、y2、y3的图象分别交于点P（x1，y1）、Q（x2，y2）、N（x3，y3），若x1＜x2＜x3，结合函数的图象，直接写出x1+x2+x3的取值范围．
【分析】本题根据图象解答，在（3）中，函数y1、y3的图象关于y轴对称，则x1+x2+x3的取值范围即为x2的取值范围．
【解答】解：（1）由图象得到点A、B坐标
故答案为：（2，2）、（﹣2，﹣2）
（2）图象如图
（3）由图象可知，若x1＜x2＜x3，
垂直于y轴的直线l在x轴与直线y＝﹣2之间
∵函数y1＝与函数y3＝﹣的图象关于y轴对称
∴x1+x3＝0
由图象﹣2＜x2＜0
∴﹣2＜x1+x2+x3＜0
【点评】本题考查了正比例函数和反比例函数图象，解答过程中要注意数形结合．
六．反比例函数的应用（共5小题）
17．（2022•青秀区校级一模）学校的自动饮水机，开机加热时每分钟上升10℃，加热到100℃，停止加热，水温开始下降．此时水温y（℃）与通电时间x（min）成反比例关系．当水温降至20℃时，饮水机再自动加热，若水温在20℃时接通电源，水温y与通电时间x之间的关系如图所示，则下列说法中正确的是（ ）
A．水温从20℃加热到100℃，需要7min
B．水温下降过程中，y与x的函数关系式是y＝
C．上午8点接通电源，可以保证当天9：30能喝到不超过40℃的水
D．在一个加热周期内水温不低于30℃的时间为min
【分析】因为开机加热时，饮水机每分钟上升10℃，所以开机加热到100℃，所用时间为＝8min，故A不合题意，利用点（8，100），可以求出反比例函数解析式，故B不符合题意，令y＝20，则x＝40，求出每40分钟，饮水机重新加热，故时间为9点30时，可以得到饮水机是第三次加热，并且第三次加热了10分钟，令x＝10，代入到反比例函数中，求出y，即可得到C不符合题意，先求出加热时间段时，水温达到30℃所用的时间，再由反比例函数，可以得到冷却时间时，水温为30℃时所对应的时间，两个时间相减，即为水温不低于30℃时的时间．
【解答】解：∵开机加热时每分钟上升10℃，
∴水温从20℃加热到100℃，所需时间为：＝8min，
故A选项不合题意；
由题可得，（8，100）在反比例函数图象上，
设反比例函数解析式为y＝，
代入点（8，100）可得，k＝800，
∴水温下降过程中，y与x的函数关系式是y＝，
故B选项不合题意；
令y＝20，则＝20，
∴x＝40，
即饮水机每经过40分钟，要重新从20℃开始加热一次，
从8点9点30分钟，所用时间为90分钟，
而水温加热到100℃，仅需要8分钟，
故当时间是9点30时，饮水机第三次加热，从20℃加热了10分钟，
令x＝10，则y＝＝80℃＞40℃，
故C选项不符合题意；
水温从20℃加热到30℃所需要时间为：min，
令y＝30，则＝30，
∴，
∴水温不低于30℃的时间为＝min，
故选：D．
【点评】本题考查了反比例函数的应用，数形结合，是解决本题的关键．
18．（2021春•邗江区期末）教室里的饮水机接通电源就进入自动程序，开机加热时每分钟上升7℃，加热到100℃，停止加热，水温开始下降，此时水温（℃）与开机后用时（min）成反比例关系．直至水温降至30℃，饮水机关机．饮水机关机后即刻自动开机，重复上述自动程序．若在水温为30℃时，接通电源后，水温y（℃）和时间（min）的关系如图，为了在上午第一节下课时（8：45）能喝到不超过50℃的水，则接通电源的时间可以是当天上午的（ ）
A．7：20B．7：30C．7：45D．8：00
【分析】先求出加热10分钟后，水温可以达到100℃，继而得到点（10，100）在如图所示的反比例函数图象上，由待定系数法求解出反比例函数解析式，进而求得当y＝30时所对应的x＝，得到每经过分钟，饮水机重新开机加热，按照此种规律，即可解决．
【解答】解：∵开机加热时每分钟上升7℃，
∴加热到100℃所需要的时间为：＝10min，
∴每次加热10min后，饮水机就会断电，开始冷却
设10分钟后，水温与开机所用时间所成的反比例函数为y＝，
∵点（10，100）在反比例函数图象上，
∴k＝1000，
∴反比例函数为，
令y＝30，则，
∴，
∴每次开机加热min后，饮水机就要重新从30℃开始加热，
如果7：20开机至8：45，经过的时间为85分钟，
85﹣＝＞10，
∴此时饮水机第三次加热，从30℃加热了分钟，
水温为y＝＝＞50℃，
故A选项不合题意，
如果7：30开机至8：45，经过的时间为75分钟，
75﹣×2＝＜10，
∴此时饮水机第三次加热了，从30℃加热了分钟，
水温为30+＝＞50℃，
故B选项不合题意，
如果7：45开机至8：45，经过的时间为60分钟，
∴此时饮水机第二次加热，从30℃加热了20分钟，
水温为y＝＝50，
故C选项符合题意，
如果8：00开机至8：45，经过的时间为45分钟，
∴此时饮水机第二次加热，从30℃加热了5分钟，
水温为y＝30+5×7＝65＞50℃，
故D选项不符合题意，
故选：C．
【点评】本题考查了反比例函数的应用，挖掘出加热时间的规律，例如本题中每经过分钟重新开机加热，是解决本题的关键．
19．（2022春•海州区校级期末）某车队要把4000吨货物运到灾区，已知每天的运输量不变．
（1）从运输开始，每天运输的货物吨数n（吨）与运输时间t（天）之间有怎样的函数表达式？
（2）因灾区道路受阻，实际每天比原计划少运20%，推迟2天完成任务，求原计划完成任务的天数．
【分析】（1）根据每天运量×天数＝总运量即可列出函数关系式；
（2）根据“实际每天比原计划少运20%，则推迟2天完成任务”列出方程求解即可．
【解答】解：（1）根据题意得：nt＝4000，
∴n＝（t＞0），
∴每天运输的货物吨数n（吨）与运输时间t（天）之间的函数表达式为n＝；
（2）设原计划x天完成，根据题意得：
（1﹣20%）＝，
解得：x＝8，
经检验：x＝8是原方程的根，
答：原计划8天完成．
【点评】本题考查了反比例函数的应用及分式方程的应用，解题的关键是找到题目中的等量关系．
20．（2021•蒸湘区校级一模）某医药研究所研制了一种新药，在试验药效时发现：成人按规定剂量服用后，检测到从第5分钟起每分钟每毫升血液中含药量增加0.2微克，第100分钟达到最高，接着开始衰退．血液中含药量y（微克）与时间x（分钟）的函数关系如图．并发现衰退时y与x成反比例函数关系．
（1）a＝ 19 ；
（2）当5≤x≤100时，y与x之间的函数关系式为 y＝0.2x﹣1 ；当x＞100时，y与x之间的函数关系式为 y＝ ；
（3）如果每毫升血液中含药量不低于10微克时是有效的，求出一次服药后的有效时间多久？
【分析】（1）利用第5分钟起每分钟每毫升血液中含药量增加0.2微克即可得到第100分钟相应的a值；
（2）分别代入直线和曲线的一般形式，利用待定系数法求得函数的解析式即可；
（3）分别令两个函数值为10求得相应的时间后相减即可得到结果．
【解答】解：（1）a＝0.2×（100﹣5）＝19；
（2）当5≤x≤100时，设y与x之间的函数关系式为y＝k1x+b
∵经过点（5，0），（100，19）
∴
解得：，
∴解析式为y＝0.2x﹣1；
当x＞100时，y与x之间的函数关系式为y＝，
∵经过点（100，19），
∴＝19
解得：k＝1900，
∴函数的解析式为y＝；
（3）令y＝0.2x﹣1＝10解得：x＝55，
令y＝＝10，解得：x＝190
∴190﹣55＝135分钟，
∴服药后能持续135分钟；
【点评】本题主要考查了反比例函数与一次函数的实际应用，根据已知点得出函数的解析式是解题关键．
21．（2021春•盱眙县期末）某蔬菜生产基地用装有恒温系统的大棚栽培一种新品，如图是某天恒温系统从开始到关闭及关闭后，大棚里温度y（℃）随时间x（h）变化的函数图象，其中AB段是恒温阶段，BC段是双曲线y＝的一部分，请根据图中信息解答下列问题：
（1）求k的值；
（2）恒温系统在一天内保持大棚内温度不低于15℃的时间有多少小时？
【分析】（1）直接将点B的坐标代入即可；
（2）观察图象可知：三段函数都有y≥15的点，而且AB段是恒温阶段，y＝20，所以计算AD和BC两段当y＝15时对应的x值，相减就是结论．
【解答】解：（1）把B（12，20）代入y＝中得：
k＝12×20＝240；
（2）如图，
设AD的解析式为：y＝mx+n．
把（0，10）、（2，20）代入y＝mx+n中得：
，
解得：，
∴AD的解析式为：y＝5x+10，
当y＝15时，15＝5x+10，x＝1．
15＝，
解得：x＝16，
16﹣1＝15．
答：恒温系统在一天内保持大棚里温度不低于15℃的时间有15小时．
【点评】本题考查了反比例函数和一次函数的性质和应用，解答此题时要先利用待定系数法确定函数的解析式，再观察图象特点，结合反比例函数和一次函数的性质作答．
七．三角形中位线定理（共1小题）
22．（2019•铁西区二模）如图，△ABC中，∠A＝60°，AC＞AB＞2，点D，E分别在边AB，AC上，且BD＝CE＝2，连接DE，点M是DE的中点，点N是BC的中点，线段MN的长为 ．
【分析】如图，作CH∥AB，连接DN，延长DN交CH于H，连接EH，作CJ⊥EH于J．首先证明CH＝EC，∠ECH＝120°，解直角三角形求出EH，利用三角形中位线定理即可解决问题．
【解答】解：如图，作CH∥AB，连接DN，延长DN交CH于H，连接EH，作CJ⊥EH于J．
∵BD∥CH，
∴∠B＝∠NCH，
∵BN＝CN，∠DNB＝∠KNC，
∵△DNB≌△HNC（ASA），
∴BD＝CH，DN＝NH，
∵BD＝EC＝2，
∴EC＝CH＝2，
∵∠A+∠ACH＝180°，∠A＝60°，
∴∠ECH＝120°，
∵CJ⊥EH，
∴EJ＝JH＝EC•cs30°＝，
∴EH＝2EJ＝2，
∵DM＝ME，DN＝NH，
∴MN＝EH＝．
故答案为．
【点评】本题考查全等三角形的判定和性质，三角形的中位线定理，解直角三角形等知识，解题的关键是学会添加常用辅助线，构造全等三角形解决问题，属于中考填空题中的压轴题．
八．平行四边形的性质（共5小题）
23．（2022春•鼓楼区期末）如图，在▱ABCD中，点D是定点，点A、C是直线l1和l2上两动点，l1∥l2，且点D到直线l1和l2的距离分别是1和4，则对角线BD长度的最小值是 5 ．
【分析】过点D作DM⊥l1于点M，延长DM交l2于点H，过点B作BN⊥l2于点N，连接MN，设CD与l1交于点E，AB与l2交于点F，证明△ADE≌△CBF（AAS），可得BN＝DM＝1，根据垂线段最短、两点之间线段最短可得，当MN⊥l1时，BD的长度取最小值，最小值为DM+BN+MH的长，进而可以解决问题．
【解答】解：如图，过点D作DM⊥l1于点M，延长DM交l2于点H，过点B作BN⊥l2于点N，连接MN，设CD与l1交于点E，AB与l2交于点F，
∵DM⊥l1，l1∥l2，
∴DM⊥l2，∠AED＝∠DCF，
∵点D是定点，且点D到直线l1和l2的距离分别是1和4，
∴DM＝1，DH＝4，
∴MH＝DH﹣DM＝4﹣1＝3，
∵四边形ABCD是平行四边形，
∴AB∥CD，AD＝BC，∠ADC＝∠CBA，
∴∠BFC＝∠DCF，
∴∠AED＝∠BFC，
在△ADE和△CBF中，
，
∴△ADE≌△CBF（AAS），
∴BN＝DM＝1，
根据垂线段最短、两点之间线段最短可得，
当MN⊥l1时，BD的长度取最小值，最小值为DM+BN+MH的长，
∴对角线BD长度的最小值是1+3+1＝5，
故答案为：5．
【点评】本题考查了平行线的性质，平行线之间的距离，解决本题的关键是掌握垂线段最短、两点之间线段最短．
24．（2022春•邗江区期末）在▱ABCD中，BC边上的高为4，AB＝5，AC＝2，则▱ABCD的周长为 12或20 ．
【分析】根据题意分别画出图形，BC边上的高在平行四边形的内部和外部，进而利用勾股定理求出即可．
【解答】解：如图1所示：
∵在▱ABCD中，BC边上的高为4，AB＝5，AC＝2，
∴EC＝＝2，AB＝CD＝5，
BE＝＝3，
∴AD＝BC＝5，
∴▱ABCD的周长等于：20，
如图2所示：
∵在▱ABCD中，BC边上的高为4，AB＝5，AC＝2，
∴EC＝＝2，AB＝CD＝5，
BE＝＝3，
∴BC＝3﹣2＝1，
∴▱ABCD的周长等于：1+1+5+5＝12，
则▱ABCD的周长等于12或20．
故答案为：12或20．
【点评】此题主要考查了平行四边形的性质以及勾股定理等知识，利用分类讨论得出是解题关键．
25．（2016•无锡）如图，已知▱OABC的顶点A、C分别在直线x＝1和x＝4上，O是坐标原点，则对角线OB长的最小值为 5 ．
【分析】过点B作BD⊥直线x＝4，交直线x＝4于点D，过点B作BE⊥x轴，交x轴于点E．则OB＝．由于四边形OABC是平行四边形，所以OA＝BC，又由平行四边形的性质可推得∠OAF＝∠BCD，则可证明△OAF≌△BCD，所以OE的长固定不变，当BE最小时，OB取得最小值，从而可求．
【解答】解：过点B作BD⊥直线x＝4，交直线x＝4于点D，过点B作BE⊥x轴，交x轴于点E，直线x＝1与OC交于点M，与x轴交于点F，直线x＝4与AB交于点N，如图：
∵四边形OABC是平行四边形，
∴∠OAB＝∠BCO，OC∥AB，OA＝BC，
∵直线x＝1与直线x＝4均垂直于x轴，
∴AM∥CN，
∴四边形ANCM是平行四边形，
∴∠MAN＝∠NCM，
∴∠OAF＝∠BCD，
∵∠OFA＝∠BDC＝90°，
∴∠FOA＝∠DBC，
在△OAF和△BCD中，
，
∴△OAF≌△BCD．
∴BD＝OF＝1，
∴OE＝4+1＝5，
∴OB＝．
由于OE的长不变，所以当BE最小时（即B点在x轴上），OB取得最小值，最小值为OB＝OE＝5．
故答案为：5．
【点评】本题考查了平行四边形的性质、坐标与图形性质、全等三角形的判定与性质；熟练掌握平行四边形的性质，证明三角形全等是解决问题的关键．
26．（2015•呼伦贝尔）如图，在平行四边形ABCD中，E、F分别为边AB、CD的中点，BD是对角线．
（1）求证：△ADE≌△CBF；
（2）若∠ADB是直角，则四边形BEDF是什么四边形？证明你的结论．
【分析】（1）由四边形ABCD是平行四边形，即可得AD＝BC，AB＝CD，∠A＝∠C，又由E、F分别为边AB、CD的中点，可证得AE＝CF，然后由SAS，即可判定△ADE≌△CBF；
（2）先证明BE与DF平行且相等，然后根据一组对边平行且相等的四边形是平行四边形，再连接EF，可以证明四边形AEFD是平行四边形，所以AD∥EF，又AD⊥BD，所以BD⊥EF，根据菱形的判定可以得到四边形是菱形．
【解答】（1）证明：∵四边形ABCD是平行四边形，
∴AD＝BC，AB＝CD，∠A＝∠C，
∵E、F分别为边AB、CD的中点，
∴AE＝AB，CF＝CD，
∴AE＝CF，
在△ADE和△CBF中，
∵
，
∴△ADE≌△CBF（SAS）；
（2）若∠ADB是直角，则四边形BEDF是菱形，理由如下：
解：由（1）可得BE＝DF，
又∵AB∥CD，
∴BE∥DF，BE＝DF，
∴四边形BEDF是平行四边形，
连接EF，在▱ABCD中，E、F分别为边AB、CD的中点，
∴DF∥AE，DF＝AE，
∴四边形AEFD是平行四边形，
∴EF∥AD，
∵∠ADB是直角，
∴AD⊥BD，
∴EF⊥BD，
又∵四边形BFDE是平行四边形，
∴四边形BFDE是菱形．
【点评】本题主要考查了平行四边形的性质，全等三角形的判定以及菱形的判定，利用好E、F是中点是解题的关键．
27．（2021春•邗江区期末）如图，在平行四边形ABCD中，∠B、∠C的平分线交于P，且分别与AD交于E、F，
（1）求证：△BPC为直角三角形；
（2）若BC＝16，CD＝3，PE＝8，求△PEF的面积．
【分析】（1）利用平行四边形的性质可得∠ABC+∠BCD＝180°，再根据角平分线的性质可得∠PBC＝∠ABC，∠BCP＝∠BCD，进而可得∠PBC+∠BCP＝90°，从而可得结论；
（2）首先证明∠ABE＝∠CBE＝∠BEA，∠DCF＝∠BCF＝∠CFD，根据等角对等边可得AB＝AE＝3，CD＝DF＝3，再计算出EF长，然后利用勾股定理计算出PF长，进而可得△PEF的面积．
【解答】（1）证明：∵四边形ABCD为平行四边形，
∴AB∥CD，
∴∠ABC+∠BCD＝180°，
∵∠B、∠C的平分线交于P，
∴∠PBC＝∠ABC，∠BCP＝∠BCD，
∴∠PBC+∠BCP＝（∠ABC+∠BCD ）＝90°，
∴∠BPC＝90°，即△BPC为直角三角形；
（2）解：∵四边形ABCD为平行四边形，
∴AD∥CB，
∴∠CBE＝∠BEA，∠BCF＝∠CFD，
∴∠ABE＝∠BEA，∠DCF＝∠CFD，
∴AB＝AE＝3，CD＝DF＝3，
∴EF＝10，
∴Rt△PEF中，PE＝8，EF＝10，
∴PF＝6，
∴△PEF的面积＝24．
【点评】此题主要考查了平行四边形的性质，以及平行线的性质，关键是掌握平行四边形两组对边平行且相等．
九．平行四边形的判定（共1小题）
28．（2020春•广宁县期末）如图，E，F是四边形ABCD对角线AC上的两点，AD∥BC，DF∥BE，AE＝CF．
求证：（1）△AFD≌△CEB；
（2）四边形ABCD是平行四边形．
【分析】（1）根据全等三角形的判定定理ASA证得△AFD≌△CEB；
（2）利用（1）中的全等三角形的对应边相等得到AD＝CB，则由“有一组对边相等且平行的四边形是平行四边形”证得结论．
【解答】证明：（1）如图，∵AD∥BC，DF∥BE，
∴∠1＝∠2，∠3＝∠4．
又AE＝CF，
∴AE+EF＝CF+EF，即AF＝CE．
在△AFD与△CEB中，
，
∴△AFD≌△CEB（ASA）；
（2）由（1）知，△AFD≌△CEB，则AD＝CB．
又∵AD∥BC，
∴四边形ABCD是平行四边形．
【点评】本题考查了全等三角形的判定与性质，平行四边形的判定．全等三角形的判定是结合全等三角形的性质证明线段和角相等的重要工具．在判定三角形全等时，关键是选择恰当的判定条件．
一十．平行四边形的判定与性质（共3小题）
29．（2022春•南京期末）如图，在▱ABCD中，AB＝6cm，AD＝10cm，点P在AD边上以每秒1cm的速度从点A向点D运动．点Q在BC边上以每秒4cm的速度从点C出发，在CB之间往返运动．两个点同时出发，当点P到达点D时停止（同时点Q也停止运动），设运动时间为t秒．当5＜t＜10时，运动时间t＝ 秒或8秒 时，以P、D、Q、B为顶点的四边形是平行四边形．
【分析】根据P的速度为每秒1cm，可得AP＝tcm，从而得到PD＝（10﹣t）cm，由四边形ABCD为平行四边形可得出PD∥BQ，结合平行四边形的判定定理可得出当PD＝BQ时以P、D、Q、B四点组成的四边形为平行四边形，当5＜t＜10时，分两种情况考虑，在每种情况中由PD＝BQ即可列出关于t的一元一次方程，解之即可得出结论．
【解答】解：∵四边形ABCD为平行四边形，
∴PD∥BQ．
若要以P、D、Q、B四点组成的四边形为平行四边形，则PD＝BQ．
当5＜t≤时，AP＝tcm，PD＝（10﹣t）cm，CQ＝（4t﹣20）cm，BQ＝（30﹣4t）cm，
∴10﹣t＝30﹣4t，
解得：t＝；
当＜t≤10时，AP＝tcm，PD＝（10﹣t）cm，BQ＝（4t﹣30）cm，
∴10﹣t＝4t﹣30，
解得：t＝8．
综上所述：当运动时间为秒或8秒时，以P、D、Q、B四点组成的四边形为平行四边形．
故答案为：秒或8秒．
【点评】本题考查了平行四边形的判定与性质以及一元一次方程的应用，弄清Q在BC上往返运动情况是解决此题的关键．
30．（2011•北京）在▱ABCD中，∠BAD的平分线交直线BC于点E，交直线DC于点F．
（1）在图1中证明CE＝CF；
（2）若∠ABC＝90°，G是EF的中点（如图2），直接写出∠BDG的度数；
（3）若∠ABC＝120°，FG∥CE，FG＝CE，分别连接DB、DG（如图3），求∠BDG的度数．
【分析】（1）根据AF平分∠BAD，可得∠BAF＝∠DAF，利用四边形ABCD是平行四边形，求证∠CEF＝∠F即可．
（2）根据∠ABC＝90°，G是EF的中点可直接求得．
（3）分别连接GB、GC，求证四边形AHFD是菱形，证明△BEG≌△DCG可得结论．
【解答】（1）证明：如图1，
∵AF平分∠BAD，
∴∠BAF＝∠DAF，
∵四边形ABCD是平行四边形，
∴AD∥BC，AB∥CD，
∴∠DAF＝∠CEF，∠BAF＝∠F，
∴∠CEF＝∠F．
∴CE＝CF．
（2）解：连接GC、BG，
∵四边形ABCD为平行四边形，∠ABC＝90°，
∴四边形ABCD为矩形，
∵AF平分∠BAD，
∴∠DAF＝∠BAF＝45°，
∵∠DCB＝90°，DF∥AB，
∴∠DFA＝45°，∠ECF＝90°
∴△ECF为等腰直角三角形，
∵G为EF中点，
∴EG＝CG＝FG，CG⊥EF，
∵△ABE为等腰直角三角形，AB＝DC，
∴BE＝DC，
∵∠CEF＝∠GCF＝45°，
∴∠BEG＝∠DCG＝135°
在△BEG与△DCG中，
∵，
∴△BEG≌△DCG，
∴BG＝DG，
∵CG⊥EF，
∴∠DGC+∠DGA＝90°，
又∵∠DGC＝∠BGA，
∴∠BGA+∠DGA＝90°，
∴△DGB为等腰直角三角形，
∴∠BDG＝45°．
（3）解：延长AB、FG交于H，连接HD．
∵AD∥GF，AB∥DF，
∴四边形AHFD为平行四边形
∵∠ABC＝120°，AF平分∠BAD
∴∠DAF＝30°，∠ADC＝120°，∠DFA＝30°
∴△DAF为等腰三角形
∴AD＝DF，
∴CE＝CF，
∴平行四边形AHFD为菱形
∴△ADH，△DHF为全等的等边三角形
∴DH＝DF，∠BHD＝∠GFD＝60°
∵FG＝CE，CE＝CF，CF＝BH，
∴BH＝GF
在△BHD与△GFD中，
∵，
∴△BHD≌△GFD，
∴∠BDH＝∠GDF
∴∠BDG＝∠BDH+∠HDG＝∠GDF+∠HDG＝60°
【点评】此题主要考查平行四边形的判定方法，全等三角形的判定与性质，等边三角形的判定与性质，菱形的判定与性质等知识点，应用时要认真领会它们之间的联系与区别，同时要根据条件合理、灵活地选择方法．同学们在解决此类问题时，可以通过以下的步骤进行思考和分析：（1）通过测量或特殊情况的提示进行猜想；（2）根据猜想的结果进行联想（如60度角可以联想到等边三角形，45度角可以联想到等腰直角三角形等）；（3）在联想的基础上根据已知条件利用几何变换（如旋转、平移、轴对称等）构造全等解决问题．
31．（2021春•溧阳市期末）如图，在△ABC中，AB＝AC＝7，BC＝5，将△ABC绕点C旋转，使得点B落在AB边上点D处，点A落在点E处，连接AE．
（1）求证：四边形ABCE是平行四边形；
（2）求△AFE的面积．
【分析】（1）证明AB∥CE，AB＝CE即可．
（2）如图，过点C作CT⊥AB于T，CK⊥DE于K，过点A作AJ⊥EF于J．证明＝，求出CT，△ACE的面积，即可解决问题．
【解答】证明：（1）∵AB＝AC，
∴∠B＝∠ACB，
∵将△ABC绕点C旋转，使得点D落在AB边上，
∴AC＝CE＝AB，∠ACB＝∠DCE，CB＝CD，
∴∠B＝∠CDB，
∴∠CDB＝∠DCE，
∴AB∥CE，
∴四边形ABCE是平行四边形．
（2）如图，过点C作CT⊥AB于T，CK⊥DE于K，过点A作AJ⊥EF于J．
∵CB＝CD＝5，CT⊥BD，
∴BT＝DT，
设BT＝x，
∵CT2＝BC2﹣BT2＝AC2﹣AT2，
∴52﹣x2＝72﹣（7﹣x）2，
∴x＝，
∴BD＝2x＝，CT＝＝＝，
∴AD＝AB﹣BD＝7﹣＝，
∵S△ADE＝•AD•CT＝•AJ•DE，
∴＝＝，
∵＝＝＝，
∵∠CDB＝∠CDE，CT⊥DB，CK⊥DE，
∴CT＝CK，
∴＝＝，
∴AF＝AC，
∴S△AEF＝S△AEC＝××7×＝．
【点评】本题考查平行四边形的判定和性质，勾股定理，三角形的面积等知识，解题的关键是求出AF：CF的值．
一十一．菱形的性质（共2小题）
32．（2021春•滨湖区期末）如图，已知菱形ABCD的面积为20，边长为5，点P、Q分别是边BC、CD上的动点，且PC＝CQ，连接PD、AQ，P、Q和C点不重合，则PD+AQ的最小值为（ ）
A．B．C．10D．
【分析】过点A作AM⊥BC于点M，延长AM到点A′，使A′M＝AM，根据菱形的性质和勾股定理可得BM＝3，以点B为原点，BC为x轴，垂直于BC方向为y轴，建立平面直角坐标系，可得B（0，0），A（3，4），C（5，0），D（8，4），A′（3，﹣4），然后证明△ABP≌△ADQ（SAS），可得AP＝AQ＝A′P，连接A′D，AP，A′P，由A′P+PD＞A′D，可得A′，P，D三点共线时，PD+A′P取最小值，所以PD+AQ的最小值＝PD+A′P的最小值＝A′D，利用勾股定理即可解决问题．
【解答】解：如图，过点A作AM⊥BC于点M，延长AM到点A′，使A′M＝AM，
∵四边形ABCD是菱形，
∴AB＝BC＝AD＝5，∠ABC＝∠ADC，
∵菱形ABCD的面积为20，边长为5，
∴AM＝4，
在Rt△ABM中，根据勾股定理得：
BM＝＝3，
以点B为原点，BC为x轴，垂直于BC方向为y轴，建立平面直角坐标系，
∴B（0，0），A（3，4），C（5，0），D（8，4），A′（3，﹣4），
∵PC＝CQ，BC＝CD，
∴BP＝DQ，
在△ABP和△ADQ中，
，
∴△ABP≌△ADQ（SAS），
∴AP＝AQ＝A′P，
连接A′D，AP，A′P，
∵A′P+PD＞A′D，
∴A′，P，D三点共线时，PD+A′P取最小值，
∴PD+AQ的最小值＝PD+A′P的最小值＝A′D＝＝．
但是当A′，P，D三点共线时，点P不在边BC上，
∵4＜＜7＜10．
故选：D．
【点评】本题考查了菱形的性质、全等三角形的判定和性质，解决本题的关键是掌握菱形的性质．
33．（2022•新市区校级三模）已知如图，在菱形ABCD中，对角线AC、BD相交于点O，DE∥AC，AE∥BD．
（1）求证：四边形AODE是矩形；
（2）若AB＝6，∠BCD＝120°，求四边形AODE的面积．
【分析】（1）先判断出四边形AODE是平行四边形，再根据菱形的对角线互相垂直可得AC⊥BD，然后根据有一个角是直角的平行四边形是矩形证明；
（2）根据两直线平行，同旁内角互补求出∠ABC＝60°，判断出△ABC是等边三角形，然后根据等边三角形的性质求出OA、OB，然后得到OD，再根据矩形的面积公式列式计算即可得解．
【解答】（1）证明：∵DE∥AC，AE∥BD，
∴四边形AODE是平行四边形，
∵在菱形ABCD中，AC⊥BD，
∴∠AOD＝90°，
∴四边形AODE是矩形；
（2）解：∵∠BCD＝120°，AB∥CD，
∴∠ABC＝180°﹣120°＝60°，
∵AB＝BC，
∴△ABC是等边三角形，
∴OA＝×6＝3，OB＝×6＝3，
∵四边形ABCD是菱形，
∴OD＝OB＝3，
∴四边形AODE的面积＝OA•OD＝3×3＝9．
【点评】本题考查了菱形的性质，矩形的判定，平行四边形的判定，主要利用了有一个角是直角的平行四边形是矩形，熟练掌握矩形，菱形与平行四边形的关系是解题的关键．
一十二．菱形的判定与性质（共1小题）
34．（2023•郧西县模拟）在Rt△ABC中，∠BAC＝90°，D是BC的中点，E是AD的中点，过点A作AF∥BC交BE的延长线于点F．
（1）证明四边形ADCF是菱形；
（2）若AC＝4，AB＝5，求菱形ADCF的面积．
【分析】（1）首先根据题意画出图形，由E是AD的中点，AF∥BC，易证得△AFE≌△DBE，即可得AF＝BD，又由在Rt△ABC中，∠BAC＝90°，D是BC的中点，可得AD＝BD＝CD＝AF，证得四边形ADCF是平行四边形，继而判定四边形ADCF是菱形；
（2）首先连接DF，易得四边形ABDF是平行四边形，即可求得DF的长，然后由菱形的面积等于其对角线积的一半，求得答案．
【解答】（1）证明：如图，∵AF∥BC，
∴∠AFE＝∠DBE，
∵E是AD的中点，AD是BC边上的中线，
∴AE＝DE，BD＝CD，
在△AFE和△DBE中，
，
∴△AFE≌△DBE（AAS）；
∴AF＝DB．
∵DB＝DC，
∴AF＝CD，
∴四边形ADCF是平行四边形，
∵∠BAC＝90°，D是BC的中点，
∴AD＝DC＝BC，
∴四边形ADCF是菱形；
（2）解：连接DF，
∵AF∥BC，AF＝BD，
∴四边形ABDF是平行四边形，
∴DF＝AB＝5，
∵四边形ADCF是菱形，
∴S＝AC•DF＝10．
【点评】此题考查了菱形的判定与性质以及全等三角形的判定与性质．注意根据题意画出图形，结合图形求解是关键．
一十三．矩形的性质（共9小题）
35．（2021春•南京期末）如图，在矩形ABCD中，E是AB的中点，动点F从点B出发，沿BC运动到点C时停止，以EF为边作▱EFGH，且点G、H分别在CD、AD上．在动点F运动的过程中，▱EFGH的面积（ ）
A．逐渐增大B．逐渐减小
C．不变D．先增大，再减小
【分析】设AB＝a，BC＝b，BE＝c，BF＝x，根据S平行四边形EFGH＝S矩形ABCD﹣2（S△BEF+S△AEH）＝（a﹣2c）x+bc，由E是AB的中点可得a﹣2c＝0，进而判断．
【解答】解：设AB＝a，BC＝b，BE＝c，BF＝x，
连接EG，
∵四边形EFGH为平行四边形，
∴EF＝HG，EF∥HG，
∴∠FEG＝∠HGE，
∵四边形ABCD为矩形，
∴AB∥CD，
∴∠BEG＝∠DGE，
∴∠BEG﹣∠FEG＝∠DGE﹣∠EGH，
∴∠BEF＝∠HGD
∵EF＝HG，∠B＝∠D，
∴Rt△BEF≌Rt△DGH（AAS），
同理Rt△AEH≌Rt△CGF，
∴S平行四边形EFGH＝S矩形ABCD﹣2（S△BEF+S△AEH）
＝ab﹣2[cx+（a﹣c）（b﹣x）]
＝ab﹣（cx+ab﹣ax﹣bc+cx）
＝ab﹣cx﹣ab+ax+bc﹣cx
＝（a﹣2c）x+bc，
∵E是AB的中点，
∴a＝2c，
∴a﹣2c＝0，
∴S平行四边形EFGH＝bc＝ab，
方法二：连接EG，
∵四边形EFGH为平行四边形，
∴EF＝HG，EF∥HG，
∴∠FEG＝∠HGE，
∵四边形ABCD为矩形，
∴AB∥CD，
∴∠BEG＝∠DGE，
∴∠BEG﹣∠FEG＝∠DGE﹣∠EGH，
∴∠BEF＝∠HGD
∵EF＝HG，∠B＝∠D，
∴Rt△BEF≌Rt△DGH（AAS），
∴DG＝BE＝CD＝AE，
∴四边形AEGD为平行四边形，
∵∠A＝90°，
∴▱AEGD为矩形，
同理四边形EBCG为矩形，
∴S平行四边形EFGH＝S△EHG+S△EFG＝EG•DG+EG•GC＝EG•DG＝EG•CD＝S矩形ABCD．
故选：C．
【点评】本题考查了矩形的性质，平行四边形的性质，解决本题的关键是掌握矩形的性质．
36．（2022春•靖江市校级期末）如图，线段AB的长为10，点D在AB上，△ACD是边长为3的等边三角形，过点D作与CD垂直的射线DP，过DP上一动点G（不与D重合）作矩形CDGH，记矩形CDGH的对角线交点为O，连接OB，则线段BO的最小值为 5 ．
【分析】连接AO，根据矩形对角线相等且互相平分得：OC＝OD，再证明△ACO≌△ADO，则∠OAB＝30°；点O一定在∠CAB的平分线上运动，根据垂线段最短得：当OB⊥AO时，OB的长最小，根据直角三角形30°角所对的直角边是斜边的一半得出结论．
【解答】解：连接AO，
∵四边形CDGH是矩形，
∴CG＝DH，OC＝CG，OD＝DH，
∴OC＝OD，
∵△ACD是等边三角形，
∴AC＝AD，∠CAD＝60°，
在△ACO和△ADO中，
，
∴△ACO≌△ADO（SSS），
∴∠OAB＝∠CAO＝30°，
∴点O一定在∠CAB的平分线上运动，
∴当OB⊥AO时，OB的长度最小，
∵∠OAB＝30°，∠AOB＝90°，
∴OB＝AB＝×10＝5，
即OB的最小值为5．
故答案为：5．
【点评】本题考查了矩形的性质、全等三角形的性质和判定、含30°角的直角三角形的性质，熟练掌握直角三角形中，30°角所对的直角边等于斜边的一半，利用了矩形对角线相等且平分的性质得对角线的一半相等，为三角形全等用铺垫；另外还利用了垂线段最短解决了求最值问题．
37．（2022•南京模拟）如图，矩形ABCD中，AB＝6，AD＝3，E为AB的中点，F为EC上一动点，P为DF中点，连接PB，则PB的最小值是 3 ．
【分析】由中位线定理可得点P的运动轨迹是线段P1P2，再由垂线段最短可得当BP⊥P1P2时，PB取得最小值，连接BP1、BP2，作BP′⊥P1P2于P′，作P2Q⊥AB于Q，则BP的最小值为BP′的长，P2Q是△EAD的中位线，由勾股定理求出BP2、BP1、CE的长，由三角形中位线定理得出P1P2的长，设P′P2＝x，则P′P1＝﹣x，由勾股定理得BP22﹣P′P22＝BP12﹣P′P12，解得x＝，即可得出结果．
【解答】解：当点F与点C重合时，点P在P1处，CP1＝DP1，
当点F与点E重合时，点P在P2处，EP2＝DP2，
∴P1P2∥CE且P1P2＝CE，
当点F在EC上除点C、E的位置处时，有DP＝FP，
由中位线定理可知：P1P∥CE且P1P＝CF，
∴点P的运动轨迹是线段P1P2，如图所示，
∴当BP⊥P1P2时，PB取得最小值，
∵四边形ABCD是矩形，
∴AD＝BC＝3，AB＝CD＝6，∠DAB＝∠BCD＝∠ABC＝90°，
∴CP1＝CD＝3，
∵E为AB的中点，
∴AE＝BE＝AB＝3，
连接BP1、BP2，作BP′⊥P1P2于P′，作P2Q⊥AB于Q，
则BP的最小值为BP′的长，P2Q是△EAD的中位线，
∴P2Q＝AD＝，QE＝AQ＝AE＝，
∴BQ＝BE+QE＝3+＝，
在Rt△BP2Q中，由勾股定理得：
BP2＝＝＝，
在Rt△CBE中，由勾股定理得：
CE＝＝＝3，
∴P1P2＝CE＝，
在Rt△BCP1中，由勾股定理得：
BP1＝＝3，
设P′P2＝x，则P′P1＝﹣x，
由勾股定理得：
BP22﹣P′P22＝BP12﹣P′P12，
即（）2﹣x2＝（3）2﹣（﹣x）2，
解得：x＝，
∴BP′2＝（）2﹣（）2＝18，
∴BP′＝3．
故答案为：3．
【点评】本题考查了矩形的性质、勾股定理、三角形中位线定理、垂线段最短等知识；熟练掌握矩形的性质和勾股定理是解题的关键．
38．（2018•邵阳模拟）如图，四边形ABCD为矩形，O为AC中点，过点O作AC的垂线分别交AD、BC于点E、F，连接AF、CE．
（1）求证：四边形AFCE是菱形．
（2）若AC＝8，EF＝6，求BF的长．
【分析】（1）由条件可先证四边形AFCE为平行四边形，再结合线段垂直平分线的性质可证得结论；
（2）由菱形的性质可求得AE＝CF＝5，设BF＝x，在Rt△ABF和Rt△ABC中，分别利用勾股定理可得到关于x的方程，可求得BF的长．
【解答】（1）证明：
∵O为AC中点，EF⊥AC，
∴EF为AC的垂直平分线，
∴EA＝EC，FA＝FC，
∴∠EAC＝∠ECA，∠FAC＝∠FCA．
∵AE∥CF，
∴∠EAC＝∠FCA，
∴∠FAC＝∠ECA，
∴AF∥CE，
∴四边形AFCE平行四边形．
又∵EA＝EC，
∴平行四边形AFCE是菱形．
（2）∵四边形AFCE是菱形，AC＝8，EF＝6，
∴OE＝3，OA＝4，
∴AE＝CF＝5，
设BF＝x，
在Rt△ABF中，AB2＝AF2﹣BF2，在Rt△ABC中，AB2＝AC2﹣BC2．
∴52﹣x2＝82﹣（x+5）2，
解得，
∴．
【点评】本题主要考查菱形的判定和性质，掌握菱形的判定方法和菱形的性质是解题的关键，在求BF的长时，注意方程思想的应用．
39．（2021春•淮安区期末）如图，在矩形ABCD中，AB＝4cm，BC＝8cm，AC的垂直平分线EF分别交AD，BC于点E，F，垂足为点O．
（1）连接AF，CE，求证：四边形AFCE为菱形；
（2）求AF的长．
【分析】（1）根据矩形的性质得出AD∥BC，求出∠AEO＝∠CFO，根据全等三角形的判定得出△AEO≌△CFO，根据全等三角形的性质得出OE＝OF，根据菱形的判定推出即可；
（2）设AF＝acm，根据菱形的性质得出AF＝CF＝acm，在Rt△ABF中，由勾股定理得出42+（8﹣a）2＝a2，求出a即可．
【解答】（1）证明：∵四边形ABCD是矩形，
∴AD∥BC，
∴∠AEO＝∠CFO，
∵AC的垂直平分线EF，
∴AO＝OC，AC⊥EF，
在△AEO和△CFO中
∵
∴△AEO≌△CFO（AAS），
∴OE＝OF，
∵O A＝OC，
∴四边形AECF是平行四边形，
∵AC⊥EF，
∴平行四边形AECF是菱形；
（2）解：设AF＝acm，
∵四边形AECF是菱形，
∴AF＝CF＝acm，
∵BC＝8cm，
∴BF＝（8﹣a）cm，
在Rt△ABF中，由勾股定理得：42+（8﹣a）2＝a2，
解得：a＝5，
即AF＝5cm．
【点评】本题考查了菱形的性质和判定，全等三角形的性质和判定，线段垂直平分线的性质，勾股定理的应用，能综合运用定理进行推理是解此题的关键，注意：对角线互相垂直的平行四边形是菱形．
40．（2019•无锡模拟）已知：如图，在平行四边形ABCD和矩形ABEF中，AC与DF相交于点G．
（1）试说明DF＝CE；
（2）若AC＝BF＝DF，求∠ACE的度数．
【分析】（1）根据平行四边形对边平行且相等可得AB＝DC，AB∥DC，矩形的对边平行且相等可得AB＝EF，AB∥EF，从而得到DC＝EF，DC∥EF，再根据一组对边平行且相等的四边形是平行四边形可得四边形DCEF是平行四边形，然后根据平行四边形对边相等证明即可；
（2）连接AE，根据矩形的对角线相等可得BF＝AE，然后求出AC＝AE＝CE，从而得到△AEC是等边三角形，再根据等边三角形的每一个角都是60°解答．
【解答】解：（1）证明：∵四边形ABCD是平行四边形，
∴AB＝DC，AB∥DC，
又∵四边形ABEF是矩形，
∴AB＝EF，AB∥EF，
∴DC＝EF，DC∥EF，
∴四边形DCEF是平行四边形，
∴DF＝CE；
（2）解：如图，连接AE，
∵四边形ABEF是矩形，
∴BF＝AE，
又∵AC＝BF＝DF，
∴AC＝AE＝CE，
∴△AEC是等边三角形，
∴∠ACE＝60°．
【点评】本题考查了矩形的性质，平行四边形判定与性质，等边三角形的判定与性质，熟记平行四边形的判定方法并准确识图是解题的关键．
41．（2011•福州）已知，矩形ABCD中，AB＝4cm，BC＝8cm，AC的垂直平分线EF分别交AD、BC于点E、F，垂足为O．
（1）如图1，连接AF、CE．求证四边形AFCE为菱形，并求AF的长；
（2）如图2，动点P、Q分别从A、C两点同时出发，沿△AFB和△CDE各边匀速运动一周．即点P自A→F→B→A停止，点Q自C→D→E→C停止．在运动过程中，
①已知点P的速度为每秒5cm，点Q的速度为每秒4cm，运动时间为t秒，当A、C、P、Q四点为顶点的四边形是平行四边形时，求t的值．
②若点P、Q的运动路程分别为a、b（单位：cm，ab≠0），已知A、C、P、Q四点为顶点的四边形是平行四边形，求a与b满足的数量关系式．
【分析】（1）先证明四边形AFCE为平行四边形，再根据对角线互相垂直平分的平行四边形是菱形作出判定；根据勾股定理即可求得AF的长；
（2）①分情况讨论可知，当P点在BF上、Q点在ED上时，才能构成平行四边形，根据平行四边形的性质列出方程求解即可；
②分三种情况讨论可知a与b满足的数量关系式．
【解答】解：（1）①∵四边形ABCD是矩形，
∴AD∥BC，
∴∠CAD＝∠ACB，∠AEF＝∠CFE，
∵EF垂直平分AC，垂足为O，
∴OA＝OC，
∴△AOE≌△COF，
∴OE＝OF，
∴四边形AFCE为平行四边形，
又∵EF⊥AC，
∴四边形AFCE为菱形，
②设菱形的边长AF＝CF＝xcm，则BF＝（8﹣x）cm，
在Rt△ABF中，AB＝4cm，
由勾股定理得42+（8﹣x）2＝x2，
解得x＝5，
∴AF＝5cm．
（2）①显然当P点在AF上时，Q点在CD上，此时A、C、P、Q四点不可能构成平行四边形；
同理P点在AB上时，Q点在DE或CE上或P在BF，Q在CD时不构成平行四边形，也不能构成平行四边形．
因此只有当P点在BF上、Q点在ED上时，才能构成平行四边形，
∴以A、C、P、Q四点为顶点的四边形是平行四边形时，PC＝QA，
∵点P的速度为每秒5cm，点Q的速度为每秒4cm，运动时间为t秒，
∴PC＝5t，QA＝CD+AD﹣4t＝12﹣4t，即QA＝12﹣4t，
∴5t＝12﹣4t，
解得，
∴以A、C、P、Q四点为顶点的四边形是平行四边形时，秒．
②由题意得，四边形APCQ是平行四边形时，点P、Q在互相平行的对应边上．
分三种情况：
i）如图1，当P点在AF上、Q点在CE上时，AP＝CQ，即a＝12﹣b，得a+b＝12；
ii）如图2，当P点在BF上、Q点在DE上时，AQ＝CP，即12﹣b＝a，得a+b＝12；
iii）如图3，当P点在AB上、Q点在CD上时，AP＝CQ，即12﹣a＝b，得a+b＝12．
综上所述，a与b满足的数量关系式是a+b＝12（ab≠0）．
【点评】本题综合性较强，考查了矩形的性质、菱形的判定与性质、勾股定理、平行四边形的判定与性质，注意分类思想的应用．
42．（2022春•工业园区期末）已知，如图，在长方形ABCD中，AB＝4，AD＝6．延长BC到点E，使CE＝3，连接DE．
（1）动点P从点B出发，以每秒1个单位的速度沿BC﹣CD﹣DA向终点A运动，设点P运动的时间为t秒，求当t为何值时，△ABP和△DCE全等？
（2）若动点P从点B出发，以每秒1个单位的速度仅沿着BE向终点E运动，连接DP．设点P运动的时间为t秒，是否存在t，使△PDE为等腰三角形？若存在，请求出t的值；否则，说明理由．
【分析】（1）若△ABP与△DCE全等，可得AP＝CE＝3或BP＝CE＝3，根据时间路程的关系可求t的值；
（2）根据题意可得：CD＝4，根据勾股定理可求DE的长；分PD＝DE，PE＝DE，PD＝PE三种情况讨论，可求t的值．
【解答】解：（1）若△ABP与△DCE全等，
∴BP＝CE或AP＝CE，
当BP＝CE＝3时，则t＝3÷1＝3，
当AP＝CE＝3时，则t＝（6+6+4﹣3）÷1＝13，
∴当t为3或13时，△ABP和△DCE全等；
（2）∵四边形ABCD是矩形，
∴AB＝CD＝4，AD＝BC＝6，CD⊥BC，
在Rt△DCE中，CE＝3，
∴DE＝＝5，
若△PDE为等腰三角形，
则PD＝DE或PE＝DE或PD＝PE，
当PD＝DE时，
∵PD＝DE，DC⊥BE，
∴PC＝CE＝3，
∵BP＝BC﹣CP＝3，
∴t＝3÷1＝3，
当PE＝DE＝5时，
∵BP＝BE﹣PE，
∴BP＝9﹣5＝4，
∴t＝4÷1＝4，
当PD＝PE时，
∴PE＝PC+CE＝3+PC，
∴PD＝3+PC，
在Rt△PDC中，DP2＝CD2+PC2．
∴（3+PC）2＝16+PC2，
∴PC＝，
∵BP＝BC﹣PC，
∴BP＝，
∴t＝÷1＝，
综上所述：当t＝3或4或时，△PDE为等腰三角形．
【点评】本题主要考查了勾股定理的应用，全等三角形和等腰三角形的判定与性质等知识，运用分类思想是解题的关键．
43．（2012•云南）如图，在矩形ABCD中，对角线BD的垂直平分线MN与AD相交于点M，与BC相交于点N，连接BM，DN．
（1）求证：四边形BMDN是菱形；
（2）若AB＝4，AD＝8，求MD的长．
【分析】（1）根据矩形性质求出AD∥BC，推出∠MDO＝∠NBO，∠DMO＝∠BNO，证△DMO≌△BNO，推出OM＝ON，得出平行四边形BMDN，推出菱形BMDN；
（2）根据菱形性质求出DM＝BM，在Rt△AMB中，根据勾股定理得出BM2＝AM2+AB2，推出x2＝x2﹣16x+64+16，求出即可．
【解答】（1）证明：∵四边形ABCD是矩形，
∴AD∥BC，∠A＝90°，
∴∠MDO＝∠NBO，∠DMO＝∠BNO，
∵在△DMO和△BNO中，
，
∴△DMO≌△BNO（AAS），
∴OM＝ON，
∵OB＝OD，
∴四边形BMDN是平行四边形，
∵MN⊥BD，
∴平行四边形BMDN是菱形．
（2）解：∵四边形BMDN是菱形，
∴MB＝MD，
设MD长为x，则MB＝DM＝x，
在Rt△AMB中，BM2＝AM2+AB2
即x2＝（8﹣x）2+42，
解得：x＝5，
所以MD长为5．
【点评】本题考查了矩形性质，平行四边形的判定，菱形的判定和性质，勾股定理等知识点的应用，对角线互相平分的四边形是平行四边形，对角线互相垂直的平行四边形是菱形．
一十四．正方形的性质（共5小题）
44．（2012•黔东南州）点P是正方形ABCD边AB上一点（不与A、B重合），连接PD并将线段PD绕点P顺时针旋转90°，得线段PE，连接BE，则∠CBE等于（ ）
A．75°B．60°C．45°D．30°
【分析】过E作AB的延长线AF的垂线，垂足为F，可得出∠F为直角，又四边形ABCD为正方形，可得出∠A为直角，进而得到一对角相等，由旋转可得∠DPE为直角，根据平角的定义得到一对角互余，在直角三角形ADP中，根据两锐角互余得到一对角互余，根据等角的余角相等可得出一对角相等，再由PD＝PE，利用AAS可得出三角形ADP与三角形PEF全等，根据确定三角形的对应边相等可得出AD＝PF，AP＝EF，再由正方形的边长相等得到AD＝AB，由AP+PB＝PB+BF，得到AP＝BF，等量代换可得出EF＝BF，即三角形BEF为等腰直角三角形，可得出∠EBF为45°，再由∠CBF为直角，即可求出∠CBE的度数．
【解答】解：过点E作EF⊥AF，交AB的延长线于点F，则∠F＝90°，
∵四边形ABCD为正方形，
∴AD＝AB，∠A＝∠ABC＝90°，
∴∠ADP+∠APD＝90°，
由旋转可得：PD＝PE，∠DPE＝90°，
∴∠APD+∠EPF＝90°，
∴∠ADP＝∠EPF，
在△APD和△FEP中，
∵，
∴△APD≌△FEP（AAS），
∴AP＝EF，AD＝PF，
又∵AD＝AB，
∴PF＝AB，即AP+PB＝PB+BF，
∴AP＝BF，
∴BF＝EF，又∠F＝90°，
∴△BEF为等腰直角三角形，
∴∠EBF＝45°，又∠CBF＝90°，
则∠CBE＝45°．
故选：C．
【点评】此题考查了正方形的性质，全等三角形的判定与性质，旋转的性质，以及等腰直角三角形的判定与性质，其中作出相应的辅助线是解本题的关键．
45．（2022春•工业园区校级期末）如图，在正方形ABCD中，AB＝4．E、F分别为边AB、BC的中点，连接AF、DE，点N、M分别为AF、DE的中点，连接MN，则MN的长度为 ．
【分析】连接AM，并延长AM交CD于点G，先通过证明△AEM≌△GDM得到DM＝EM，DG＝AE后，证明MN是△AGF的中位线，可得MN＝GF，在Rt△FCG中利用勾股定理求出GF的长，从而求出MN的长．
【解答】解：连接AM并延长AM交CD于点G，连接GF，如图所示，
∵四边形ABCD是正方形，
∴CD＝BC＝AB＝4，∠C＝90°，AB∥CD，
∴∠AEM＝∠GDM，
∵E、F分别为边AB、BC的中点，
∴AE＝AB＝2，CF＝BC＝2．
∵M为DE的中点，
∴EM＝DM，
在△EAM和△DGM中，
．
∴△EAM≌△DGM（SAS）．
∴AM＝MG，DG＝AE＝2．
∴M为AG的中点，
∵N为AF的中点，
∴MN是△AGF的中位线．
∴MN＝GF．
在Rt△FCG中，
CG＝DC﹣DG＝4﹣2＝2，
∴GF＝＝2．
∴MN＝GF＝．
故答案为：．
【点评】本题考查了正方形的性质、全等三角形的判定与性质与勾股定理的应用，难度较大，解答本题的关键是添加辅助线把MN归纳到三角形中，然后证明MN是三角形的中位线．
46．（2022春•仪征市期末）在正方形ABCD中，点E，F在对角线AC上，AC＝12．
（1）如图（1），若BE＝BF，则AE与CF相等吗？请说明理由；
（2）如图（2），若∠EBF＝45°，CF＝4，求EF的长；
（3）如图（3），若点E，F是AC的三等分点，点P在正方形ABCD的边上从点A开始按逆时针方向运动一周，直至返回点A，试求此过程中满足PE+PF为整数的点P个数．
【分析】（1）连接BD，利用正方形的性质和等腰三角形的性质和等式的性质解答即可；
（2）将△BCF绕着点B逆时针旋转90°得到△BAG，连接EG，利用旋转的性质和全等三角形的判定与性质和勾股定理解答即可；
（3）先求得点P在边AB上运动时，PE+PF为整数时的P的个数，再利用对称性即可得出结论．
【解答】解：（1）AE＝CF，理由：
连接BD，如图，
∵四边形ABCD是正方形，
∴AC⊥BD，OA＝OC．
∵BE＝BF，
∴OE＝OF，
∴OA﹣OE＝OC﹣OF．
即：AE＝BF．
（2）将△BCF绕着点B逆时针旋转90°得到△BAG，连接EG，如图，
则△BCF≌△BGA，
∴∠ABG＝∠FBC，∠GAB＝∠FCB＝45°，BG＝BF，
∴∠GAE＝∠GAB+∠BAC＝45°+45°＝90°，
∵∠ABC＝90°，∠EBF＝45°，
∴∠ABE+∠CBF＝45°，
∴∠GBA+∠ABE＝45°，
即：∠GBE＝45°，
∴∠GBE＝∠FBE＝45°．
在△GBE和△FBE中，
，
∴△GBE和△FBE（SAS），
∴GE＝EF，AG＝CF＝4．
设EF＝BG＝x，则AE＝AC﹣CF﹣EF＝8﹣x，
在Rt△AGE中，
∵AG2+AE2＝GE2，
∴42+（8﹣x）2＝x2，
解得：x＝5，
∴EF＝5；
（3）当P，A两点重合时，PE+PF＝4+8＝12，符合题意；
当点P在A，B两点之间时，
作点E关于AB的对称点E′，连接E′F交AB于点P，如图，
则此时PE+PF的值最小，
∵点E关于AB的对称点E′，
∴AE′＝AE＝4，PE′＝PE，AB⊥E′E，
∴∠E′AB＝∠EAB＝45°，
∴∠E′AE＝90°，
∴PE+PF＝PE′+PF＝E′F＝＝4＜9；
当P，B两点重合时，连接BD交AC于点O，如图，
则OE＝OA﹣AE＝2，OB＝OA＝6，
∴PE＝BE＝＝2，
同理，PF＝2，
∴PE+PF＝4＜13，不符合题意，
∴点P在AB边上运动时，4≤PE+PF≤4，则符合题意的点有8个（包括点A），
由对称性可知，在正方形的四边上符合题意的点有：7×4+2＝30．
【点评】本题主要考查了正方形的性质，等腰三角形的性质，直角三角形的性质，全等三角形的判定与性质，图形的对称与旋转的性质，熟练掌握正方形的性质是解题的关键．
47．（2022春•海门市期末）如图，正方形ABCD中，E是对角线BD上一点，连接AE，过点E作EF⊥AE，交边BC于点F．
（1）求证：EA＝EF；
（2）写出线段FC，DE的数量关系并加以证明；
（3）若AB＝4，FE＝FC，求DE的长．
【分析】（1）过点E作MN⊥AD于M，交BC于点N，由四边形ABCD为正方形，AE⊥EF，可证明△AEM≌△EFN（ASA），即可得AE＝EF．
（2）由△AEM≌△EFN，∠ADB＝45°，可得CF＝2MD，而DE＝MD，故CF＝DE；
（3）设DE＝x可得：FE2＝AE2＝AM2+ME2＝（4﹣x）2+（x）2，而CF＝DE，若FE＝FC，有（4﹣x）2+（x）2＝（x）2，可解得DE＝2﹣2．
【解答】（1）证明：过点E作MN⊥AD于M，交BC于点N，如图：
∵四边形ABCD为正方形，
∴AD∥BC，AD＝DC，∠ADB＝45°，
∵MN⊥AD，
∴MN⊥BC，
∴四边形NCDM为矩形，
∴MN＝CD，
∵∠ADB＝45°，MN⊥AD，
∴MD＝ME，
∴AM＝EN，
∵AE⊥EF，
∴∠AEM+∠FEN＝90°．
∵∠AEM+∠MAE＝90°，
∴∠FEN＝∠MAE，
∴△AEM≌△EFN（ASA），
∴AE＝EF．
（2）解：CF＝DE，理由如下：
由（1）知△AEM≌△EFN，∠ADB＝45°，
∴ME＝FN＝MD，
∵四边形NCDM为矩形，
∴CN＝MD，
∴CF＝2MD，
∵DE＝MD，
∴CF＝DE；
（3）解：设DE＝x．由（1）得：FE2＝AE2＝AM2+ME2＝（4﹣x）2+（x）2，
由（2）得CF＝DE，
∴CF＝x，
∵FE＝FC，
∴FE2＝FC2，
∴（4﹣x）2+（x）2＝（x）2，
解方程得：x1＝2﹣2，x2＝﹣2﹣2（舍去），
∴DE＝2﹣2．
【点评】本题考查正方形性质及应用，涉及全等三角形的判定与性质，勾股定理及应用等，解题的关键是作辅助线，构造三角形全等．
48．（2022春•太仓市期末）如图，在正方形ABCD中，AB＝，E为正方形ABCD内一点，DE＝AB，∠EDC＝α（0°＜α＜90°），连结CE，AE，过点D作DF⊥AE，垂足为点F，交CE的延长线于点G，连结AG．
（1）当α＝20°时，求∠DAE的度数；
（2）判断△AEG的形状，并说明理由；
（3）当GF＝1时，求CE的长．
【分析】（1）由正方形的性质，求出∠ADE＝70°，再根据三角形内角和定理求解即可即可求解．
（2）由等腰三角形的性质可得DG是AE的垂直平分线，可得AG＝GE，由四边形内角和定理，可求∠GEA＝45°，即可求解．
（3）由正方形的性质和等腰直角三角形的性质可求AC，AG的长，在Rt△ACG中，利用勾股定理可求解．
【解答】解：（1）∵四边形ABCD是正方形，
∴∠ADC＝90°，AB＝AD，
∵∠CDE＝20°，
∴∠ADE＝70°，
∵DE＝AB，
∴DA＝DE，
∴∠DAE＝∠DEA＝×（180°﹣70°）＝55°．
（2）结论：△AEG是等腰直角三角形．
理由：∵AD＝DE，DF⊥AE，
∴DG是AE的垂直平分线，
∴AG＝GE，
∴∠GAE＝∠GEA，
∵DE＝DC＝AD，
∴∠DAE＝∠DEA，∠DEC＝∠DCE，
∵∠DAE+∠DEA+∠DEC+∠DCE+∠ADC＝360°，
∴∠DEA+∠DEC＝135°，
∴∠GEA＝45°，
∴∠GAE＝∠GEA＝45°，
∴∠AGE＝90°，
∴△AEG为等腰直角三角形．
（3）如图，连接AC，
∵四边形ABCD是正方形，
∴AC＝AB＝，
∵△AEG为等腰直角三角形，GF⊥AE，
∴GF＝AF＝EF＝1，
∴AG＝GE＝，
∵AC2＝AG2+GC2，
∴10＝2+（EC+）2，
∴EC＝（负根已经舍弃）．
【点评】本题考查了正方形性质，等腰直角三角形的性质，勾股定理等知识，添加恰当辅助线构造直角三角形是解题的关键．
一十五．正方形的判定（共2小题）
49．（2022春•隆安县期末）如图，四边形ABCD是平行四边形，AE∥BD，AE与CB的延长线交于点E，DE交AB于F．
（1）求证：BC＝BE；
（2）连接CF，若∠ADF＝∠BCF且AD＝2AF，求证：四边形ABCD是正方形．
【分析】（1）根据平行四边形的性质得：AD∥BC，AD＝BC，又由平行四边形的判定得：四边形AEBD是平行四边形，又由平行四边形的对边相等可得结论；
（2）根据（1）：四边形AEBD是平行四边形，对角线互相平分可得：AF＝BF＝AB，EF＝FD，从而证明AD＝AB，即邻边相等，证明EF＝FC＝FD，得∠FDC＝∠FCD，从而∠BCD＝90°，根据有一个角是直角，邻边相等的平行四边形是正方形可得结论．
【解答】证明：（1）∵四边形ABCD是平行四边形，
∴AD∥BC，AD＝BC，
∵AE∥BD，
∴四边形AEBD是平行四边形，
∴AD＝EB，
∴BC＝BE；
（2）由（1）知：四边形AEBD是平行四边形，
∴AF＝BF＝AB，EF＝FD，
∵AD＝2AF，
∴AB＝AD，
∵AD∥EC，
∴∠ADF＝∠BCF，
∴∠FEC＝∠BCF，
∴EF＝FC＝FD，
∴∠FDC＝∠FCD，
∴∠ADF+∠FDC＝∠FCD+∠BCF，
即∠ADC＝∠BCD，
∵AD∥BC，
∴∠ADC+∠BCD＝180°，
∴∠BCD＝90°，
∴四边形ABCD是正方形．
【点评】此题考查了平行四边形的性质、正方形的判定、等腰三角形的判定与性质、平行线的性质，属于基础题，正确利用平行四边形的性质是解题关键．
50．（2008•乌鲁木齐）如图，在四边形ABCD中，点E是线段AD上的任意一点（E与A，D不重合），G，F，H分别是BE，BC，CE的中点．
（1）证明：四边形EGFH是平行四边形；
（2）在（1）的条件下，若EF⊥BC，且EF＝BC，证明：平行四边形EGFH是正方形．
【分析】通过中位线定理得出GF∥EH且GF＝EH，所以四边形EGFH是平行四边形；当添加了条件EF⊥BC，且EF＝BC后，通过对角线相等且互相垂直平分（EF⊥GH，且EF＝GH）就可证明是正方形．
【解答】证明：（1）∵G，F分别是BE，BC的中点，
∴GF∥EC且GF＝EC．
又∵H是EC的中点，EH＝EC，
∴GF∥EH且GF＝EH．
∴四边形EGFH是平行四边形．
（2）连接GH，EF．
∵G，H分别是BE，EC的中点，
∴GH∥BC且GH＝BC．
又∵EF⊥BC且EF＝BC，
又∵EF⊥BC，GH是三角形EBC的中位线，
∴GH∥BC，
∴EF⊥GH，
又∵EF＝GH．
∴平行四边形EGFH是正方形．
【点评】主要考查了平行四边形的判定和正方形的性质．正方形对角线的特点是：对角线互相垂直；对角线相等且互相平分；每条对角线平分一组对角．
一十六．正方形的判定与性质（共1小题）
51．（2022春•仪征市期末）我们知道菱形与正方形的形状有差异，可以将菱形与正方形的接近程度称为菱形的“接近度”．如图，已知菱形ABCD的边长为5，设菱形ABCD的对角线BD，AC的长分别为m，n（m≥n）．若我们将菱形的“接近度”定义为，即“接近度”＝．
（1）当菱形的“接近度”＝ 1 时，菱形就是正方形；
（2）在菱形ABCD中，∠ABC＝60°，求此菱形的“接近度”；
（3）若菱形ABCD的“接近度”是2，求此时菱形ABCD面积．
【分析】（1）根据当菱形的“接近度”等于1时，菱形ABCD的对角线BD，AC的长相等，进而得出答案；
（2）利用菱形性质可得△ABC是等边三角形，进而可以解决问题；
（3）根据当菱形的“接近度”等于2，菱形ABCD的边长为5，可得菱形对角线长，进而得出答案．
【解答】解：（1）当菱形的“接近度”＝1时，菱形的对角线相等，此时菱形就是正方形；
故答案为：1；
（2）在菱形ABCD中，∠ABC＝60°，
∴△ABC是等边三角形，
∴该菱形形ABCD的“接近度”等于；
（3）若菱形ABCD的“接近度”是2，
∵菱形ABCD的边长为5，
∴菱形ABCD的对角线BD，AC的长分别为4，2，
此时菱形ABCD面积＝4×2＝20．
【点评】此题主要考查了菱形的性质以及新定义，利用“接近度”定义求出是解题关键．
一十七．旋转的性质（共7小题）
52．（2022•苏州模拟）如图，正方形ABCD的边长为4，∠BCM＝30°，点E是直线CM上一个动点，连接BE，线段BE绕点B顺时针旋转45°得到BF，连接DF，则线段DF长度的最小值等于（ ）
A．4﹣4B．2﹣2C．2D．2
【分析】如图，连接BD，在BD上截取BG，使得BG＝BC，连接FG，过点D作DH⊥GF于点H．证明△CBE≌△GBF（SAS），推出∠BCE＝∠BGF＝30°，推出点F在直线GF上运动，当点F与H重合时，DF的值最小，作出DH即可解决问题．
【解答】解：如图，连接BD，在BD上截取BG，使得BG＝BC，连接FG，过点D作DH⊥GF于点H．
∵四边形ABCD是正方形，
∴∠CBD＝45°，CD＝CB＝4，∠DCB＝90°，
∴BD＝4，BG＝BC＝4，
∴DG＝BD﹣BG＝4﹣4，
∵∠CBG＝∠EBF＝45°，
∴∠CBE＝∠GBF，
在△CBE和△GBF中，
，
∴△CBE≌△GBF（SAS），
∴∠BCE＝∠BGF＝30°，
∴点F在直线GF上运动，当点F与H重合时，DF的值最小，
∵DH⊥FH，∠DGH＝∠BGF＝30°
∴DH＝DG＝2﹣2，
∴DF的最小值为2﹣2，
故选：B．
【点评】本题考查旋转的性质，全等三角形的判定和性质，正方形的性质等知识，解题的关键是学会添加常用辅助线，构造全等三角形解决问题，属于中考常考题型．
53．（2022•南京模拟）在长方形ABCD中，AB＝4，BC＝3，CE＝2BE，EF＝2，连接AF，将线段AF绕着点A顺时针旋转90°得到AP，则线段PE的最小值为（ ）
A．2B．﹣2C．4D．+1
【分析】连接AE，过点A作AG⊥AE，截取AG＝AE，连接PG，GE，通过SAS证明△AEF≌△AGP，得PG＝EF＝2，再利用勾股定理求出GE的长，在△GPE中，利用三边关系即可得出答案．
【解答】解：连接AE，过点A作AG⊥AE，截取AG＝AE，连接PG，GE，
∵将线段AF绕着点A顺时针旋转90°得到AP，
∴AF＝AP，∠PAF＝90°，
∴∠FAE+∠PAE＝∠PAE+∠PAG＝90°，
∴∠FAE＝∠PAG，
在△AEF和△AGP中，
，
∴△AEF≌△AGP（SAS），
∴PG＝EF＝2，
∵BC＝3，CE＝2BE，
∴BE＝1，
在Rt△ABE中，由勾股定理得：
AE＝，
∵AG＝AE，∠GAE＝90°，
∴GE＝＝，
在△GPE中，PE＞GE﹣PG，
∴PE的最小值为GE﹣PG＝﹣2，
故选：B．
【点评】本题主要考查了旋转的性质，全等三角形的判定与性质，三角形的三边关系等知识，作辅助线构造出全等三角形是解题的关键．
54．（2022•常熟市模拟）如图，在Rt△ABC中，∠ACB＝90°，∠ABC＝30°，AC＝2，点P是边AB上的一动点．△A'B'C≌△ABC，将△A'B′C绕点C按逆时针方向旋转，点E是边A'C的中点，则PE长度的最小值为 ﹣1 ．
【分析】过点C作CD⊥AB于点D，在Rt△ACD中，根据CD＝ACsin∠BAC求出CD的长，当P在AB上运动至垂足点D，△A'B'C绕点C旋转，当点C、E、D共线时DE最小，即PE最小，据此求解可得．
【解答】解：过点C作CD⊥AB于点D，如图：
∵Rt△ABC中，∠B＝30°，
∴∠BAC＝60°，
∵Rt△ACD中，AC＝2，
∴CD＝AC•sin∠BAC＝2×＝，
当点P在AB上运动到点D，△A'B'C绕点C旋转，点C、E、D共线时DE最小，即PE最小，最小值为CD﹣CE＝﹣1，
故答案为：﹣1．
【点评】本题考查的是图形的旋转、锐角三角函数的定义等知识，根据题意得出点P运动至点D、△A'B'C绕点C旋转到点C、E、D共线时，D′E最小，即PE最小是解题的关键．
55．（2022春•邗江区期末）如图，在△ABC中，∠ACB＝90°，AC＝3cm，BC＝4cm．将△ABC绕点C按逆时针方向旋转后得△DCE，直线DA、BE相交于点F．取BC的中点G，连接GF，则GF长的最大值为 4 cm．
【分析】设∠BCE＝∠ACD＝α，可得∠CBE＝∠CEB＝∠CAD＝∠CDA＝90°﹣α，根据四边形内角和可得∠BFA＝90°，取AB的中点H，连接HG、HF，则HG＝AC，HF＝AB，继而可得FG≤HG+HF，即可得到答案．
【解答】解：取AB的中点H，连接HG、HF，如图：
∵△DEC是由△ABC绕C点旋转得到，
∴CE＝CB，CD＝CA，∠BCE＝∠ACD，
设∠BCE＝∠ACD＝α，则∠CBE＝∠CEB＝∠CAD＝∠CDA＝90°﹣α，
在四边形BCDF中，∠BFA＝360°﹣∠BCD﹣∠CDA﹣∠CBE＝360°﹣（90°+α）﹣2（90°﹣α）＝90°，
在Rt△ABC中，∠ACB＝90°，BC＝4cm，AC＝3cm，
∴AB＝5cm，
Rt△ABF中，HF＝AB＝cm，
∵HG是△ABC中位线，
∴HG＝AC＝cm，
而FG≤HF+HG＝4cm，
∴当F、H、G在一条直线上时，FG最大，最大值为HF+HG＝4cm，
故答案为：4．
【点评】本题主要考查旋转的性质、直角三角形的性质及勾股定理、中位线定理，构建以FG为边的三角形，根据三角形三边关系得出FG的长度范围是解题的关键．
56．（2022•平邑县一模）在正方形ABCD中，点E在射线BC上（不与点B、C重合），连接DB，DE，将DE绕点E逆时针旋转90°得到EF，连接BF．
（1）如图1，点E在BC边上．
①依题意补全图1；
②若AB＝6，EC＝2，求BF的长；
（2）如图2，点E在BC边的延长线上，用等式表示线段BD，BE，BF之间的数量关系．
【分析】（1）①根据要求画出图形即可；
②过点F作FH⊥CB，交CB的延长线于H．证明△DCE≌△EHF（AAS），推出EC＝FH，DC＝EH，推出CE＝BH＝FH，再利用勾股定理解决问题即可；
（2）由②可得△DCE≌△EHF，推出EC＝FH，DC＝EH，推出CE＝BH＝FH，再利用等腰直角三角形的性质解决问题即可
【解答】解（1）图形如图所示．
过点F作FH⊥CB，交CB的延长线于H，
∵四边形ABCD是正方形，
∴CD＝AB＝6，∠C＝90°，
∵∠DEF＝∠C＝90°，
∴∠DEC+∠FEH＝90°，∠DEC+∠EDC＝90°，
∴∠FEH＝∠EDC，
在△DEC和△EFH中，
，
∴△DEC≌△EFH（AAS），
∴EC＝FH＝2，CD＝BC＝EH＝6，
∴HB＝EC＝2，
∴Rt△FHB中，BF＝＝＝2．
（2）结论：BF+BD＝BE．
理由：过点F作FH⊥CB，交CB于H，
∵四边形ABCD是正方形，
∴CD＝AB＝6，∠DCE＝90°，
∵∠DEF＝∠DCE＝90°，
∴∠DEC+∠FEH＝90°，∠DEC+∠EDC＝90°，
∴∠FEH＝∠EDC，
在△DEC和△EFH中，
，
∴△DEC≌△EFH（AAS），
∴EC＝FH，CD＝BC＝EH，
∴HB＝EC＝HF，
∴△DCB和△BHF都是等腰直角三角形，
∴BD＝BC＝HE，BF＝BH，
∵HE+BH＝BE，
∴BF+BD＝BE．
【点评】本题考查作图﹣旋转变换，全等三角形的判定和性质，等腰直角三角形的性质和判定等知识，解题的关键是学会添加常用辅助线，构造全等三角形解决问题．
57．（2016春•工业园区期末）如图，在△ABC中，∠BAC＝50°，将△ABC绕点A按逆时针方向旋转后得△AB1C1．当B1B∥AC时，求∠BAC1的度数．
【分析】先依据平行的性质可求得∠ABB1的度数，然后再由旋转的性质得到△AB1B为等腰三角形，∠B1AC1＝50°，再求得∠BAB1的度数，最后依据∠BAC1＝∠BAB1﹣∠C1AB1求解即可．
【解答】解：∵B1B∥AC，
∴∠ABB1＝∠BAC＝50°．
∵由旋转的性质可知：∠B1AC1＝∠BAC＝50°，AB＝AB1．
∴∠ABB1＝∠AB1B＝50°．
∴∠BAB1＝80°
∴∠BAC1＝∠BAB1﹣∠C1AB1＝80°﹣50°＝30°．
【点评】本题主要考查的是旋转的性质、平行线的判断，求得∠BAB1的度数是解题的关键．
58．（2021•厦门二模）在正方形ABCD中，将边AD绕点A逆时针旋转α（0°＜α＜90°）得到线段AE，AE与CD延长线相交于点F，过B作BG∥AF交CF于点G，连接BE．
（1）如图1，求证：∠BGC＝2∠AEB；
（2）当（45°＜α＜90°）时，依题意补全图2，用等式表示线段AH，EF，DG之间的数量关系，并证明．
【分析】（1）根据BG∥AF，得到∠GBE＝∠AEB，由AD绕点A逆时针旋转α得到线段AE，得到AE＝AB，∠ABE＝∠AEB＝∠GBE，由正方形性质得到CD∥AB，得到∠BGC＝2∠AEB；
（2）按照题意补全图形即可，在DC上取DN＝AH，连接AN交BG于M，交BE于P，连接HM，EM，利用△ADN≌△BAH、△ABP≌△MBP、△ABH≌△MBH证明A、H、M、B共圆，从而可得∠DNA＝∠GMN，GN＝GM，再证明EF＝GM，即可得到EF＝AH+DG．
【解答】解：（1）证明：∵边AD绕点A逆时针旋转α（0°＜α＜90°）得到线段AE，
∴AD＝AE，
∵正方形ABCD，
∴AB＝AD＝AE，
∴∠AEB＝∠ABE，
∵BG∥AF，
∴∠AEB＝∠GBE，
∴∠ABE＝∠AEB＝∠GBE，
∴∠ABG＝2∠AEB，
∵正方形ABCD，
∴AB∥CD，
∴∠BGC＝∠ABG，
∴∠BGC＝2∠AEB；
（2）补全图2如下：
线段AH，EF，DG之间的数量关系为：EF＝AH+DG，理由如下：
在DC上取DN＝AH，连接AN交BG于M，交BE于P，连接HM，EM，如图：
∵正方形ABCD，
∴AB＝AD，∠ADN＝∠BAH＝90°，
又DN＝AH，
∴△ADN≌△BAH（SAS），
∴∠DNA＝∠AHB，∠DAN＝∠ABH，
∵∠DNA+∠DAN＝90°，
∴∠DAN+∠AHB＝90°，
∴∠APH＝90°，
∴∠BPM＝∠BPA＝90°，
由（1）知∠ABE＝∠GBE，
且BP＝BP，
∴△ABP≌△MBP（ASA），
∴AB＝MB，
而BH＝BH，∠ABE＝∠GBE，
∴△ABH≌△MBH（SAS），
∴∠HAB＝∠HMB＝90°，
∴A、H、M、B共圆，
∴∠AHB＝∠AMB＝∠GMN，
∴∠DNA＝∠GMN，
∴GN＝GM，
∵CF∥AB，BG∥AF，
∴四边形ABGF是平行四边形，
∴BG＝AF，
∵AE＝AD＝AB＝MB，
∴EF＝GM，
∴EF＝GN，
∵GN＝DG+DN，
∴EF＝DG+AH．
【点评】本题考查正方形性质应用及全等三角形的性质和判定，难度较大，解题的关键是构造辅助线，将AH+DG转化为GN．
一十八．作图-旋转变换（共1小题）
59．（2022春•盱眙县期末）如图，在平面直角坐标系中，已知△ABC的三个顶点的坐标分别为A（﹣5，1），B（﹣2，2），C（﹣1，4），请按下列要求画图：
（1）将△ABC先向右平移4个单位长度、再向下平移1个单位长度，得到△A1B1C1，画出△A1B1C1；
（2）△A2B2C2与△ABC关于原点O成中心对称，画出△A2B2C2．
【分析】（1）根据点平移的规律得到A1（﹣1，0），B1（2，1），C1（3，3），然后描点即可；
（2）根据关于原点对称的点的坐标特征得到A2（5，﹣1），B2（2，﹣2），C2（1，﹣4），然后描点即可．
【解答】解：（1）如图：
（2）如图：
【点评】本题考查了作图﹣旋转变换：根据旋转的性质可知，对应角都相等都等于旋转角，对应线段也相等，由此可以通过作相等的角，在角的边上截取相等的线段的方法，找到对应点，顺次连接得出旋转后的图形．也考查了平移变换．
一十九．条形统计图（共1小题）
60．（2022春•盱眙县期末）我市中小学全面开展“阳光体育”活动，某校在大课间中开设了A（体操）、B（乒乓球）、C（毽球）、D（跳绳）四项活动．为了解学生最喜欢哪一项活动，随机抽取了部分学生进行调查，并将调查结果绘制成了如下两幅不完整的统计图，请根据统计图回答下列问题：
（1）这次被调查的学生共有 400 人；
（2）请将统计图2补充完整；
（3）统计图1中B项目对应的扇形的圆心角是 108 度；
（4）已知该校共有学生1000人，根据调查结果估计该校喜欢体操的学生有 100 人．
【分析】（1）由C项目的人数及其百分比可得答案；
（2）先根据D项目百分比及总人数求得D项目人数，再依据各项目人数之和等于总人数得出A项目的人数，即可补全图形；
（3）用360度乘以样本中B项目人数占总人数的比例即可得；
（4）用总人数乘以样本中A项目人数所占比例即可．
【解答】解：（1）这次被调查的学生共有160÷40%＝400（人），
故答案为：400；
（2）D项目的人数为400×20%＝80（人），
则A项目的人数为400﹣（120+160+80）＝40（人），
补全图形如下：
（3）统计图1中B项目对应的扇形的圆心角是×360°＝108°，
故答案为：108；
（4）根据调查结果估计该校喜欢体操的学生有1000×＝100（人），
故答案为：100．
【点评】本题考查的是条形统计图和扇形统计图的综合运用，读懂统计图，从不同的统计图中得到必要的信息是解决问题的关键．条形统计图能清楚地表示出每个项目的数据；扇形统计图直接反映部分占总体的百分比大小．