浙教新版2023-2024学年九年级上册数学期末复习试卷(含解析)

这是一份浙教新版2023-2024学年九年级上册数学期末复习试卷(含解析)，共18页。试卷主要包含了如果m等内容，欢迎下载使用。
1．平面内有两点P，O，⊙O的半径为5，若PO＝6，则点P与⊙O的位置关系是（ ）
A．圆内B．圆上
C．圆外D．圆上或圆外
2．如果m：n＝1：2，那么下列各式中不成立的是（ ）
A．B．C．D．
3．将二次函数y＝x2﹣4x﹣4的图象先向上平移3个单位长度，再向右平移2个单位长度得到的图象对应的二次函数的表达式为y＝x2+ax+b，则ab的值为（ ）
A．﹣22B．22C．88D．﹣88
4．在4张相同的卡片上分别写有数﹣1、﹣3、4、6，将卡片的背面朝上并洗匀，从中抽取一张，抽到的数是奇数的概率（ ）
A．B．C．D．1
5．如图，△ABC的顶点A，B，C均在⊙O上，若∠ABC+∠AOC＝90°，则∠AOC的大小是（ ）
A．70°B．60°C．45°D．30°
6．如图，△ABC中DE∥BC，在线段BC上任取一点P，连接AP交DE于点N，下列结论错误的是（ ）
A．＝B．＝C．＝D．＝
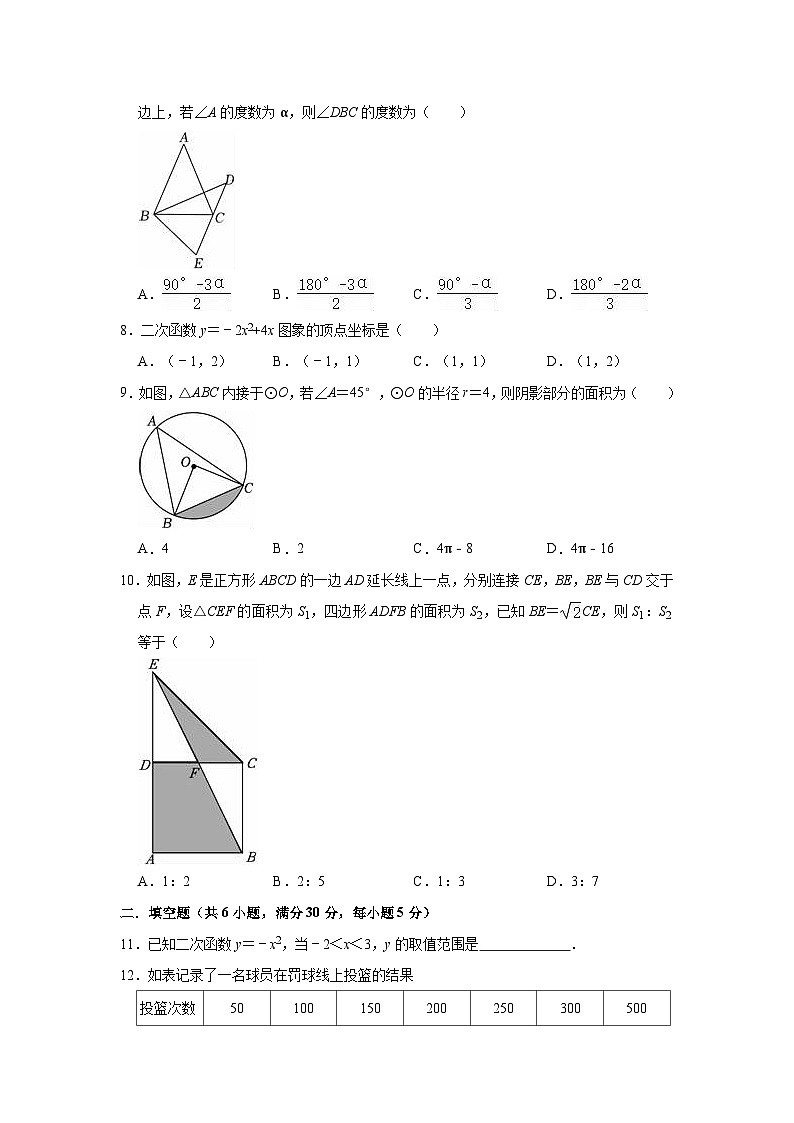
7．如图，等腰三角形ABC绕底角顶点B顺时针旋转一个角度得到三角形DBE，点C在DE边上，若∠A的度数为α，则∠DBC的度数为（ ）
A．B．C．D．
8．二次函数y＝﹣2x2+4x图象的顶点坐标是（ ）
A．（﹣1，2）B．（﹣1，1）C．（1，1）D．（1，2）
9．如图，△ABC内接于⊙O，若∠A＝45°，⊙O的半径r＝4，则阴影部分的面积为（ ）
A．4B．2C．4π﹣8D．4π﹣16
10．如图，E是正方形ABCD的一边AD延长线上一点，分别连接CE，BE，BE与CD交于点F，设△CEF的面积为S1，四边形ADFB的面积为S2，已知BE＝CE，则S1：S2等于（ ）
A．1：2B．2：5C．1：3D．3：7
二．填空题（共6小题，满分30分，每小题5分）
11．已知二次函数y＝﹣x2，当﹣2＜x＜3，y的取值范围是 ．
12．如表记录了一名球员在罚球线上投篮的结果
那么这位运动员在罚球线上投篮一次，进球的概率约为 （结果保留小数点后一位）．
13．如图1所示的铝合金窗帘轨道可以直接弯曲制作成弧形．若制作一个圆心角为160°的圆弧形窗帘轨道（如图2）需用此材料800πmm，则此圆弧所在圆的半径为 mm．
14．如图，在⊙O中，C是弦AB上一点，AC＝2，CB＝8．连接OC，过点C作DC⊥OC，与⊙O交于点D，DC的长为 ．
15．抛物线的顶点在原点，且过点（3，﹣27），则这条抛物线的解析式为 ．
16．某新建小区里安装了一架秋千，图是一个小孩荡秋千的侧面示意图，秋千的链子OA的长度为3米，秋千向两边摆动的最大角度相同，且最大角度的和∠BOC恰好为90°，则它摆至最高位置与最低位置的高度之差是 ．
三．解答题（共8小题，满分80分）
17．如图，⊙O的弦AB、CD的延长线相交于点P，且PA＝PC．求证：＝．
18．某游戏有个摸球的环节，现有四个分别标有数字4，﹣2，﹣3，5的小球，它们除数字外其余全部相同，现将它们放入一个不透明的布袋中，搅匀后从袋中随机地摸取一个不放回，将该小球上的数字记为a，再随机地摸取一个，将小球上的数字记为b．
（1）请你用列表法或树状图法写出（a，b）所有可能的结果；
（2）求所选出的a，b能使坐标点（a，b）落在第四象限的概率．
19．如图，在△ABC中，∠C＝90°，AC＝12cm，BC＝16cm，D、E分别是AC、AB的中点，连接DE．点P从点D出发，沿DE方向匀速运动，速度为2cm/s；同时，点Q从点B出发，沿BA方向匀速运动，速度为4cm/s，当点P停止运动时，点Q也停止运动．连接PQ，设运动时间为t（0＜t＜4）s．解答下列问题：
（1）当t为何值时，以点E、P、Q为顶点的三角形与△ADE相似？
（2）当t为何值时，△EPQ为等腰三角形？
20．如图，在每个边长都为1的正方形组成的网格中，小正方形的顶点叫做格点．线段AB的端点A、B均在格点上．
（1）线段AB的长等于 ．
（2）将线段AB逆时针旋转90°得到线段BC，在图中画出BC，并连接AC．
（3）在线段AB上确定一点D，连接CD，使得△BCD和△ACD的面积比为4：3．
要求：以上作图只用无刻度的直尺画图，保留作图痕迹，不写画法．
21．如图，在平面直角坐标系中，已知抛物线y＝x2+bx+c与直线AB相交于A，B两点，其中A（﹣3，﹣4），B（0，﹣1）．
（1）求该抛物线的函数表达式．
（2）点P为直线AB下方抛物线上的任意一点，连接PA，PB，求△PAB面积的最大值．
（3）在二次函数的对称轴上找一点C，使得△ABC是等腰三角形，求满足条件的点C的坐标．
22．如图，△ABC内接于⊙O（AC＞BC），AB是⊙O的直径，E，C，D是⊙O上的点，，连结ED分别交AC，AB于点F，G．
（1）求证：△EFA∽△BCA．
（2）若BC＝5，BG＝4，求AE的长．
23．某超市准备销售一种儿童玩具，进货价格为每件40元，并且每件的售价不低于进货价．经过市场调查，每月的销售量y（件）与每件的售价x（元）之间满足如图所示的函数关系．
（1）求每月的销售量y（件）与每件的售价x（元）之间的函数关系式；（不必写出自变量的取值范围）
（2）物价部门规定，该儿童玩具每件的利润不允许高于进货价的60%．设销售这种儿童玩具每月的总利润为w（元），那么每件售价定为多少元可获得最大利润？最大利润是多少？
24．在菱形ABCD中，∠ABC＝60°，点P是对角线BD上一动点，将线段CP绕点C顺时针旋转120°到CQ，连接DQ．
（1）如图1，求证：△BCP≌△DCQ；
（2）如图2，连接QP并延长，分别交AB、CD于点M、N．
①求证：PM＝QN；
②若MN的最小值为2，直接写出菱形ABCD的面积为 ．
参考答案与试题解析
一．选择题（共10小题，满分40分，每小题4分）
1．解：∵⊙O的半径为5，若PO＝6，
∴6＞5，
∴点P与⊙O的位置关系是点P在⊙O外，
故选：C．
2．解：∵m：n＝1：2，
∴＝，
A．当m＝2，b＝4时，＝＝，故此选项错误；
B，，故本选项正确；
C，＝＝＝2，故本选项正确；
D，，故本选项正确；
故选：A．
3．解：∵y＝x2﹣4x﹣4＝（x﹣2）2﹣8，
∴将抛物线y＝（x﹣2）2﹣8先向上平移3个单位长度，再向右平移2个单位长度得到：y＝（x﹣2﹣2）2﹣8+3，即y＝x2﹣8x+11，
∴a＝﹣8，b＝11，
故ab＝﹣8×11＝﹣88．
故选：D．
4．解：∵共有4张相同的卡片，分别写有数﹣1、﹣3、4、6，其中奇数有﹣1、﹣3，共有2个，
∴从中抽取一张，抽到的数是奇数的概率是＝．
故选：B．
5．解：∵∠ABC＝∠AOC，
而∠ABC+∠AOC＝90°，
∴∠AOC+∠AOC＝90°，
∴∠AOC＝60°．
故选：B．
6．解：∵DE∥BC，
在线段BC上任取一点P，连接AP交DE于点N，
∴＝，
＝，
∵＝，＝，
∴＝．
∴选项A、B、C都正确，
因为＝，
所以D选项错误．
故选：D．
7．解：∵AB＝AC，∠A＝α，
∴∠ABC＝∠ACB＝，
由旋转性质知BC＝BE，∠DBE＝∠E＝∠ABC＝∠ACB＝，
∴∠BCE＝∠E＝，
∴∠CBE＝180°﹣∠BCE﹣∠E＝α，
∴∠DBC＝∠DBE﹣∠CBE＝﹣α＝，
故选：B．
8．解：∵y＝﹣2x2+4x＝﹣2（x﹣1）2+2，
∴顶点坐标为（1，2），
故选：D．
9．解：∵∠A＝45°，
∴∠BOC＝2∠A＝90°，
∵⊙O的半径r＝4，
∴阴影部分的面积＝扇形BOC的面积﹣△BOC的面积
＝﹣OB•OC
＝4π﹣×4×4
＝4π﹣8，
故选：C．
10．解：设AB＝a，DE＝x，
∵四边形ABCD是正方形，
∴AB＝BC＝CD＝AD＝a，CD∥AB，
∴∠CDE＝∠A＝90°，AE＝a+x，
∴BE2＝AB2+AE2＝a2+（a+x）2，CE2＝CD2+DE2＝a2+x2，
∵BE＝CE，
∴BE2＝2CE2，
∴a2+（a+x）2＝2（a2+x2），
解关于x的方程得x＝2a或x＝0（不符合题意，舍去），
∴DE＝2a，
∵DF∥AB，
∴△DFE∽△ABE，
∴＝＝＝，
∴DF＝a，CF＝a﹣a＝a，
∴S1＝S△CEF＝×a×2a＝a2，S2＝S四边形ADFB＝a（a+a）＝a2，
∴S1：S2＝a2： a2＝2：5，
故选：B．
二．填空题（共6小题，满分30分，每小题5分）
11．解：∵二次函数y＝﹣x2中a＝﹣1＜0，
∴抛物线开口向下，有最大值为0，抛物线的对称轴为y轴，
当﹣2＜x＜3时，对应图象在对称轴的两侧，
当x＝﹣2时，y＝﹣4，
当x＝3时，y＝﹣9
∴当﹣2＜x＜3，y的取值范围是﹣9＜y≤0，
故答案为﹣9＜y≤0．
12．解：根据题意得：
＝0.56，＝0.6，＝0.52，＝0.492，≈0.507，＝0.502，
由上数据可得，进球的概率约为0.5；
故答案为：0.5．
13．解：设此圆弧所在圆的半径为R mm，
由弧长公式得：＝800π，
解得：R＝900，
即此圆弧所在圆的半径为900mm，
故答案为：900．
14．解：延长DC交⊙O于点E．
∵OC⊥DE，
∴DC＝CE，
连接AD、BE，则∠ADE＝∠ABE，
∵∠ACD＝∠ECB，
∴△ADC∽△EBC，
∴＝，
∵AC•CB＝DC•CE，
∴DC2＝2×8＝16，
∵DC＞0，
∴DC＝4，
故答案为4．
15．解：∵抛物线的顶点在原点，
∴设抛物线的表达式：y＝ax2，
∵抛物线过点（3，﹣27），
∴9a＝﹣27，
∴a＝﹣3，
∴y＝﹣3x2，
故答案为：y＝﹣3x2．
16．解：连接BC交OA于点M．
∵OB＝OC，∠AOB＝∠AOC，
∴OA⊥BC，
∴BM＝MC，
∴OM＝BC，
∵∠BOC＝90°，OB＝OC＝3，
∴BC＝＝3，
∴OM＝，
∴AM＝OA﹣OM＝3﹣，
故答案为：（3﹣）米．
三．解答题（共8小题，满分80分）
17．证明：连接AC、OA、OB、OC、OD，如图所示，
∵PA＝PC，
∴∠PAC＝∠PCA，
∵∠PAC＝∠BOC，∠PCA＝∠AOD，
∴∠BOC＝∠AOD，
∴＝，
∴﹣＝﹣，即＝．
18．解：（1）列表如下：
由图表知，共有12种等可能的结果数；
（2）共有12种等可能的结果数，其中点（a，b）落在第四象限的有（4，﹣3）（5，﹣3）（4，﹣2）（5，﹣2），共4种情况，
则所选出的a，b能使坐标点（a，b）落在第四象限的概率是＝．
19．解：（1）如图1中，
在Rt△ABC中，AC＝12cm，BC＝16cm，
∴AB＝＝20cm．
∵D、E分别是AC、AB的中点．
AD＝DC＝6cm，AE＝EB＝10cm，DE∥BC且
DE＝BC＝8cm，
①PQ⊥AB时，
∵∠PQB＝∠ADE＝90°，∠AED＝∠PEQ，
∴△PQE∽△ADE，
∴，由题意得：PE＝8﹣2t，QE＝4t﹣10，
即，
解得t＝；
②如图2中，当PQ⊥DE时，△PQE∽△DAE，
∴，
∴，
∴t＝，
∴当t为s或s时，以点E、P、Q为顶点的三角形与△ADE相似．
（2）如图3中，当点Q在线段BE上时，由EP＝EQ，可得8﹣2t＝10﹣4t，t＝1．
如图4中，当点Q在线段AE上时，由EQ＝EP，可得8﹣2t＝4t﹣10，解得t＝3．
如图5中，当点Q在线段AE上时，由EQ＝QP，可得（8﹣2t）：（4t﹣10）＝4：5，解得t＝．
如图6中，当点Q在线段AE上时，由PQ＝EP，可得（4t﹣10）：（8﹣2t）＝4：5，解得t＝．
综上所述，t＝1或3或或秒时，△PQE是等腰三角形．
20．解：（1）线段AB的长＝＝，
故答案为；
（2）如图，线段BC即为所求；
（3）如图，点D即为所求．
取点E，F，连接AE，BF使得AE＝3，BF＝4，
连接EF与AB交于点D，
∵AE∥BF，
∴△BDF∽△ADE，
∴＝＝，
∴×BD•BC：×AD•BC＝4：3，
∴△BCD和△ACD的面积比为4：3．
21．解：（1）将A（﹣3，﹣4），B（0，﹣1）代入y＝x2+bx+c，
得，
解得，
∴y＝x2+4x﹣1；
（2）设直线AB的解析式为y＝kx+b，
则，
解得，
∴y＝x﹣1，
设P（a，a2+4a﹣1），则Q（a，a﹣1），
∴PQ＝﹣a2﹣3a，
∴S△PAB＝×3×（﹣a2﹣3a）＝﹣（a+）2+，
∴当a＝﹣时，△PAB的面积有最大值；
（3）设点C（﹣2，y），
∵A（0，﹣1），B（﹣3，﹣4），
∴AB2＝32+32＝18，BC2＝22+（y+1）2，AC2＝12+（y+4）2，
①当AB＝BC时，
∴22+（y+1）2＝18，
解得，
∴；
②当AB＝AC时，
∴12+（y+4）2＝18，
解得，
∴；
③当BC＝AC时，
∴22+（y+1）2＝12+（y+4）2，
解得y＝﹣2，
∴C（﹣2，﹣2）；
综上所述：C点坐标为或或（﹣2，﹣2）．
22．（1）证明：∵，
∴∠EAC＝∠BAC，∠E＝∠CBA，
∴△EFA∽△BCA．
（2）解：∵AB为⊙O直径，
∴∠ACB＝90°．
∵△EFA∽△BCA．
∴∠EFA＝∠C＝90°，．
又∵∠CAE＝∠CAB，AF＝AF，
∴△AEF≌△AFG（ASA），
∴AE＝AG，EF＝FG．
∵∠AEG＝∠ABD，∠AGE＝∠BGD，
∴△AEG∽△DBG，
∴，
设EF＝FG＝2x．AE＝AG＝5x，
∴AB＝5x+4，
∴，
∴x＝，
∴．
23．解：（1）由图象可知每月销售y（件）与售价x（元）之间为一次函数关系，设其函数关系式为y＝kx+b（k≠0），
将（50，600），（70，400）代入，得：
，
解得：，
∴每月销售y（件）与售价x（元）的函数关系式为y＝﹣10x+1100；
（2）由题意得：
w＝y（x﹣40）＝（﹣10x+1100）（x﹣40）
＝﹣10x2+1500x﹣44000
＝﹣10（x﹣75）2+12250，
∵﹣10＜0，
∴当x≤75时，w随x的增大而增大，
∵该玩具每件的售价不低于进货价且每件利润不允许高于进货价的60%，
∴40≤x≤40（1+60%），
解得40≤x≤64，
∴当x＝64时，w取得最大值，此时w＝11040，
答：每件售价定为64元可获得最大利润，最大利润是11040元．
24．（1）证明：四边形ABCD是菱形，
∴BC＝DC，AB∥CD，
∴∠PBM＝∠PBC＝∠ABC＝30°，∠ABC+∠BCD＝180°，
∴∠BCD＝180°﹣∠ABC＝120°，
由旋转的性质得：PC＝QC，∠PCQ＝120°，
∴∠BCD＝∠PCQ，
∴∠BCP＝∠DCQ，
在△BCP和△DCQ中，，
∴△BCP≌△DCQ（SAS）；
（2）①证明：由（1）得：△BCP≌△DCQ，
∴BP＝DQ，
∠QDC＝∠PBC＝∠PBM＝30°．
在CD上取点E，使QE＝QN，如图2所示：
则∠QEN＝∠QNE，
∴∠QED＝∠QNC＝∠PMB，
在△PBM和△QDE中，，
∴△PBM≌△QDE （AAS），
∴PM＝QE＝QN．
②解：由①知PM＝QN，
∴MN＝PQ＝PC，
∴当PC⊥BD时，PC最小，此时MN最小，
则PC＝2，BC＝2PC＝4，
∴菱形ABCD的面积＝2S△ABC＝2××42＝8；
故答案为：8．
投篮次数n
50
100
150
200
250
300
500
进球次数m
28
60
78
104
123
152
251
﹣3
﹣2
4
5
﹣3
（﹣3，﹣2）
（﹣3，4）
（﹣3，5）
﹣2
（﹣2，﹣3）
（﹣2，4）
（﹣2，5）
4
（4，﹣3）
（4，﹣2）
（4，5）
5
（5，﹣3）
（5，﹣2）
（5，4）