第1章 平行线 单元小结 浙教版七年级数学下册课件

这是一份第1章 平行线 单元小结 浙教版七年级数学下册课件，共37页。
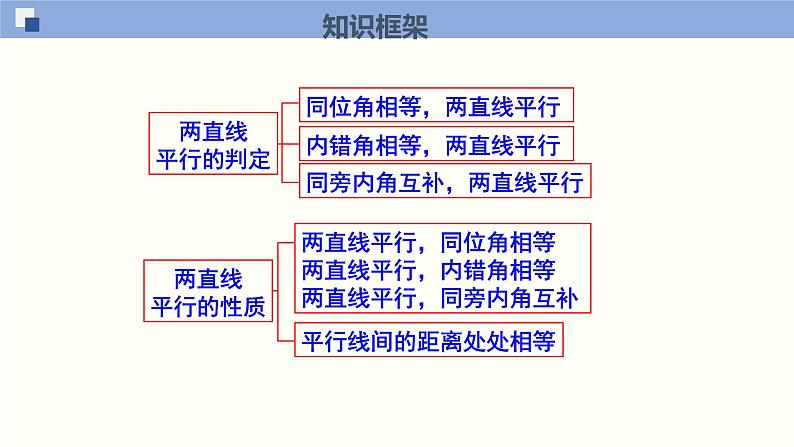
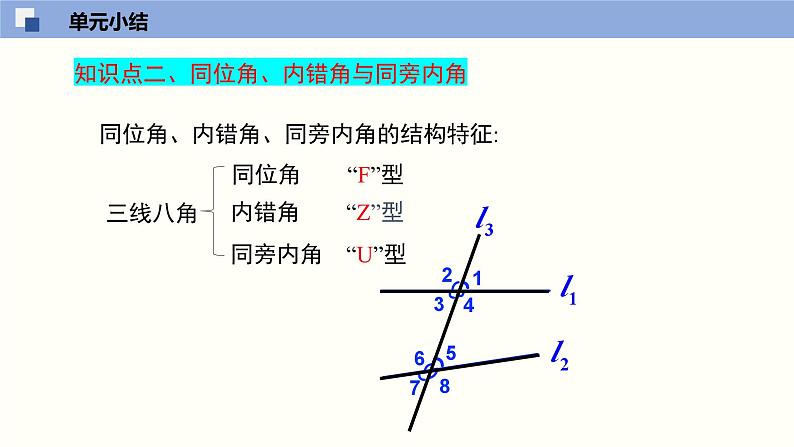
单元小结数学（浙教版）七年级 下册第1章 平行线知识框架两直线平行的判定同位角相等，两直线平行同旁内角互补，两直线平行两直线平行的性质两直线平行，同位角相等两直线平行，内错角相等两直线平行，同旁内角互补平行线间的距离处处相等内错角相等，两直线平行单元小结知识点一 平行线的相关概念概念：在同一平面内，永不相交的两条直线叫做平行线；平行线的定义包括三个基本特征：一是在同一平面内；二是两条直线；三是不相交。 在同一平面内，两条直线的位置关系只有两种：平行和相交。 单元小结平行公理：经过直线外一点，有且只有一条直线平行于这条直线.平行公理的推论：如果两条直线和第三条直线平行，那么这两条直线平行.单元小结知识点二、同位角、内错角与同旁内角同位角、内错角、同旁内角的结构特征:同位角 “F”型内错角 “Z”型同旁内角 “U”型三线八角单元小结知识点三、平行线的判定与性质1.在同一平面内，_______的两条直线叫作平行线.3.平行于同一条直线的两条直线_______.2.经过直线外一点，________一条直线与已知直线平行.4.平行线的判定与性质：两直线平行 同位角相等内错角相等同旁内角互补平行线的判定平行线的性质不相交有且只有平行单元小结知识点四、 平移的相关概念1.平移的概念：在平面内，将一个图形沿某个方向移动一定的距离，这样的图形运动称为平移.2.平移的性质：(1)平移前后的图形的形状和大小完全相同;(2)对应线段平行且相等.单元小结【例1】在平面内，下列四个说法中，正确的是（　　）A．经过一点有且只有一条线段与已知直线垂直B．经过一点有且只有一条线段与已知直线平行C．经过一点有且只有一条直线与已知直线垂直D．经过一点有且只有一条直线与已知直线平行【详解】解：A．经过一点有且只有一条直线与已知直线垂直，不是线段，故本选项错误；B．经过直线外一点有且只有一条直线与已知直线平行，既要求经过直线外一点，要是直线，故本选项错误；C．经过一点有且只有一条直线与已知直线垂直，故本选项正确；D．经过直线外一点有且只有一条直线与已知直线平行，故本选项错误；故选：C．单元小结针对训练1．平行公理：经过直线外一点，有且只有_____条直线与已知直线平行．平行公理的推论（平行线的传递性）：如果两条直线都与第三条直线平行，那么这两条直线互相_____．几何语言表示：∵a∥c ， c∥b（已知）∴_____∥_____（如果两条直线都和第三条直线平行，那么这两条直线也互相平行）【答案】     一     平行     a     b单元小结【例2】如图，直线a，b被直线c所截，下列说法不正确的是（    ）A．∠1与∠2是内错角 B．∠3与∠4是同旁内角C．∠2与∠5是同位角 D．∠2与∠4是内错角单元小结【答案】A【分析】根据同旁内角、同位角、内错角的定义逐项分析即可解答．【详解】A、∠1与∠2是对顶角，故原说法错误，符合题意；B、∠3与∠4是同旁内角，故原说法正确，不符合题意；C、∠2与∠5是同位角，故原说法正确，不符合题意；D、∠2与∠4是内错角，故原说法正确，不符合题意．故答案为A．单元小结针对训练2．如图，有下列判断：①∠A与∠1是同位角；②∠A与∠B是同旁内角；③∠4与∠C是内错角；④∠2与∠3是对顶角．其中正确的是______（填序号）．单元小结【答案】①②④【分析】根据同位角、同旁内角、内错角、对顶角的定义判断即可．【详解】解：①由同位角的概念得出，∠A与∠1是同位角，正确；②由同旁内角的概念得出，∠A与∠B是同旁内角，正确；③由同旁内角的概念得出，∠4与∠C是同旁内角，错误；④由对顶角的概念得出，∠2与∠3是对顶角，正确．故正确的是①②④．故答案为：①②④．单元小结【例3】如图，现有条件：①∠B+∠BCD=180°；②∠1=∠2；③∠3=∠4；④∠D=∠5．能判断的条件有（   ）A．①② B．②③ C．①③ D．②④单元小结【详解】①∵∠B+∠BCD=180°∴AB∥CD②∵∠1=∠2∴AD∥BC③∵∠3=∠4∴AB∥CD④∵∠D=∠5∴AD∥BC∴能得到AB∥CD的条件是①③．故选C．单元小结针对训练3．如图，直线α、b被直线c所截，∠2=65°，当∠1=______°时，α∥b．【详解】解：如图，若要α∥b，则∠1+∠3=180°， ∵∠2=65°，∴∠3=180°-65°=115°， ∴∠1=∠3=115°．故答案为：115．单元小结【例1】下列说法正确的是（    ）A．过一点有且只有一条直线与已知直线平行B．垂直于同一条直线的两条直线互相平行C．从直线外一点到这条直线的垂线段，叫做这点到这条直线的距离D．在平面内过一点有且只有一条直线与已知直线垂直单元小结【详解】解：A、过直线外一点，有且只有一条直线与已知直线平行，故此选项错误；B、在同一平面内，垂直于同一条直线的两条直线互相平行，故此选项错误；C、从直线外一点到这条直线的垂线段长，叫做这点到这条直线的距离，故此选项错误；D、在平面内过一点有且只有一条直线与已知直线垂直，故此选项正确．故选：D．单元小结针对训练4．已知直线α、b、c在同一平面内，如果α⊥c，b⊥c，那么直线α、b的位置关系是________．【详解】如图，∵α⊥c，∴∠1=90°， ∵b⊥c∴∠2=90°∴∠1=∠2∴α∥b故答案为：平行．单元小结【例5】如图，已知AB∥CD∥EF，∠1=60°，∠3=20°，则∠2的度数是（    ）A．105° B．120° C．135° D．140°单元小结【详解】解：∵AB∥EF，∠1=60°，∴∠AEF=∠1=60°，∵∠3=20°，∴∠CEF=60°-20°=40°，∵CD∥EF，∴∠2+∠CEF=180°∴∠2=180°-40°=140°．故选D．单元小结针对训练5．如图，已知AB∥CD，点M，N分别在直线AB、CD上，∠MEN=90°，∠CNE=∠ENF，则∠α与∠β的数量关系________．单元小结 单元小结【例6】如图，将△ABC沿水平方向向右平移到△DEF的位置（A与D、B与E，C与F分别是对应点）．已知点A，D之间的距离为2，BC=2BE，则BF的长为（    ）A．6 B．5 C．4 D．3单元小结【详解】解：∵△ABC沿水平方向向右平移到△DEF，点A，D之间的距离为2，∴BE=CF=2，∵BC=2BE=4，∴BF=BC+CF=6，故选：A．单元小结针对训练6．如图，△ABC沿BC方向平移得到△DEF．若BF=13，EF=9，则EC的长是 _____．【详解】解：∵△ABC沿BC方向平移得到△DEF，∴BC=EF=9，∵BF=13，∴BE=4，∴EC=5．故答案为：5单元小结1．如图，将△ABC沿直线AB的方向向右平移后到达△BDE的位置．(1)若AD=6cm，则平移的距离=___________cm．(2)若∠CAB=50°，∠BDE=100°，求∠CBE的度数．单元小结【详解】（1）解：∵将△ABC沿直线AB的方向向右平移后到达△BDE的位置．∴△ABC≌△BDE，∴AB=BD，∵AD=6cm，∴AB=BD=3cm则平移的距离为3cm，故答案为：3．（2）由（1）知，△ABC≌△BDE∴∠DBE=∠CAB=50°，∠ABC=∠DBE=100°，∴∠CBE=180°-∠ABC-∠DBE=30°．单元小结2．把下面的证明过程补充完整：已知：如图，∠1+∠2=180°，∠C=∠D，求证：∠A=∠F．证明：∵∠1+∠2=180°（已知），∴BD∥CE（______），∴∠C=∠ABD（______），∵∠C=∠D（已知），∴______（等量代换），∴AC∥DF（______），∴∠A=∠F（______）．单元小结【详解】证明：∵∠1+∠2=180°（已知），∴BD∥CE（同旁内角互补，两直线平行），∴∠C=∠ABD（两直线平行，同位角相等），∵∠C=∠D（已知），∴∠ABD=∠D（等量代换），∴AC∥DF（内错角相等，两直线平行），∴∠A=∠F（两直线平行，内错角相等）．故答案为：同旁内角互补，两直线平行；两直线平行，同位角相等；；内错角相等，两直线平行；两直线平行，内错角相等．单元小结3．如图，在△ABC中，CG⊥AB，垂足为 G，点 F 在BC上，EF⊥AB，垂足为 E．(1)GC与EF平行吗？为什么？(2)如果∠1=∠2，且∠3=60°，求∠ACB的度数．单元小结【详解】（1）解：GC∥EF，理由如下：∵CG⊥AB，EF⊥AB，∴GC∥EF；（2）解：∵GC∥EF，∴∠GCB=∠2，∵∠1=∠2，∴∠1=∠GCB，∴GD∥BC，∴∠ACB=180°-∠3=120°．单元小结4．已知 AM∥CN，点B在直线AM、CN之间，∠ABC=88°．(1)如图1，请直接写出∠A和∠C之间的数量关系：_________．(2)如图2，∠A和∠C满足怎样的数量关系？请说明理由．(3)如图3，AE平分∠MAB，CH平分∠NCB，AE与CH交于点G，则∠AGH的度数为_________．单元小结【详解】（1）解：过点B作BE∥AM，如图，∴∠A=∠ABE．∵BE∥AM，AM∥CN，∴BE∥AM∥CN．∴∠C=∠CBE．∵∠ABC=88°．∴∠A+∠C=88°故答案为：88°；单元小结（2）解：∠A和∠C满足：∠C-∠A=92°．理由：过点B作BE∥AM，如图，∴∠A=∠ABE∵BE∥AM，AM∥CN，∴BE∥AM∥CN．∴∠C+∠CBE=180°．∴∠CBE=180°-∠C．∵∠ABC=88°．∴∠ABE+∠CBE=88°．∴∠A+180°-∠C=88°．∴∠C-∠A=92°；单元小结 谢 谢~