北师大版八年级下册2 平行四边形的判定教案配套课件ppt

这是一份北师大版八年级下册2 平行四边形的判定教案配套课件ppt，共23页。PPT课件主要包含了复习回顾，对角线，推进新课，归纳小结，随堂练习，课堂小结等内容，欢迎下载使用。

1.什么是平行四边形？
两组对边分别平行的四边形叫做平行四边形.
2.我们学习了平行四边形的哪些性质？
平行四边形的两组对边分别相等；
平行四边形的两组对角分别相等；
∵四边形ABCD是平行四边形 ∴AB=CD，AD=BC .
∵四边形ABCD是平行四边形 ∴∠A=∠C，∠D=∠B .
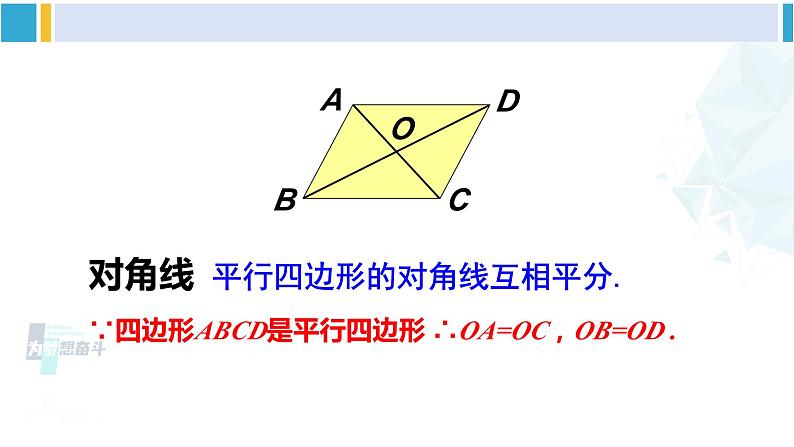
平行四边形的对角线互相平分.
∵四边形ABCD是平行四边形 ∴OA=OC，OB=OD .
我们已经学习了平行四边形的这些性质，那么它们的逆命题各是什么呢？
两组对角分别相等的四边形是平行四边形；
对角线互相平分的四边形是平行四边形.
两组对边分别相等的四边形是平行四边形；
我们得到的这些逆命题都成立吗？我们一起探讨一下吧！
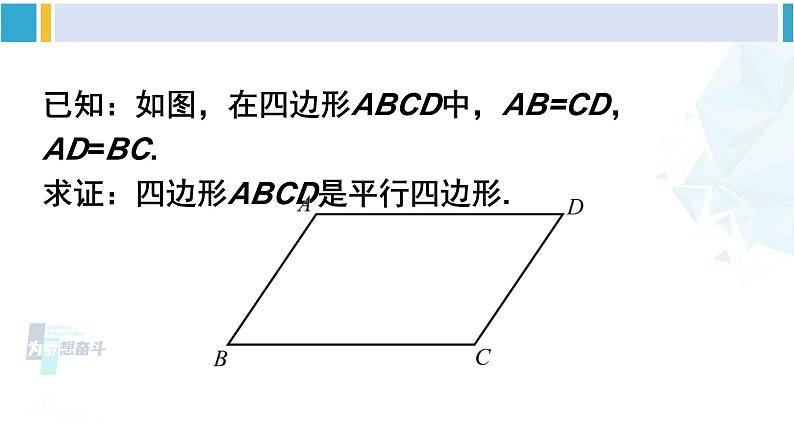
已知：如图，在四边形ABCD中，AB=CD，AD=BC.求证：四边形ABCD是平行四边形.
证明：如图，连接BD，在△ABD和△CDB中∵ AB=CD，AD=BC，BD=DB，∴△ABD≌ △CDB.∴∠1=∠2，∠3=∠4.∴AB∥CD，AD∥CB.∴四边形ABCD是平行四边形（平行四边形的定义）.
定理 两组对边分别相等的四边形是平行四边形.
已知：如图，在四边形ABCD中，AB=CD，AB∥CD.求证：四边形ABCD是平行四边形.
证明：如图，连接AC.∵ AB∥CD，∴∠BAC = ∠DCA.又∵AB = CD，AC = CA，∴△ABC≌△CDA，∴BC = DA.∴四边形ABCD是平行四边形（两组对边分别相等的四边形是平行四边形）.
定理 一组对边平行且相等的四边形是平行四边形.
两组对边分别平行的四边形是平行四边形；
AD∥BC AB∥DC
四边形ABCD是平行四边形
AD = BC AB = DC
一组对边平行且相等的四边形是平行四边形；
AD∥BC AD = BC
证明：∵ 四边形ABCD是平行四边形，∴AD = CB（平行四边形的对边相等）， AD∥CB（平行四边形的定义）.∵E，F 分别是AD和CB的中点，∴ED= AD，FB= CB.∴ED = FB，ED∥FB.∴四边形BFDE是平行四边形（一组对边平行且相等的四边形是平行四边形）.
1. 如图，线段AD是线段BC经过平移得到的，分别连接AB，CD，四边形ABCD是平行四边形吗？请说明理由.
2. 如图，AC=BD，AB=CD=EF，CE=DF.图中有哪些互相平行的线段？请说明理由.
1.已知:在平行四边形ABCD中，点 E，F，G，H分别是AB，BC，CD，DA的中点.则下图中有几个平行四边形？
解：9个，分别是四边形ABFH，DCFH，AEGD，BEGC，ABCD，AEOH，DGOH，BEOF，CGOF.
2.已知：在四边形ABCD中，AB∥CD，要使四边形ABCD为平行四边形，需添加一个条件是什么？
解：AD∥BC或AB=CD
3. □ ABCD的对角线相交于点O，点E、F、G、H分别是OA、OB、OC、OD的中点。四边形EFGH是平行四边形吗？为什么？
答：四边形EFGH是平行四边形.理由是：∵四边形ABCD是平行四边形，∴AB∥CD，AB=CD.又∵点E,F,G,H分别是OA,OB,OC,OD的中点，∴EF=1/2AB，EF∥AB. GH=1/2CD，GH∥CD.∴EF∥GH，EF=GH.∴四边形EFGH是平行四边形.
平行四边形的判定方法：