北师大版九年级数学下册 第一章 直角三角形的边角关系 第一课时 方向角问题（课件）

这是一份北师大版九年级数学下册 第一章 直角三角形的边角关系 第一课时 方向角问题（课件），共14页。
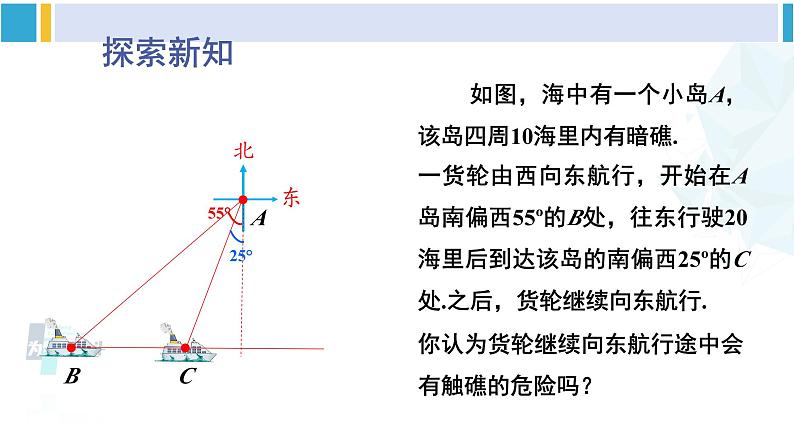
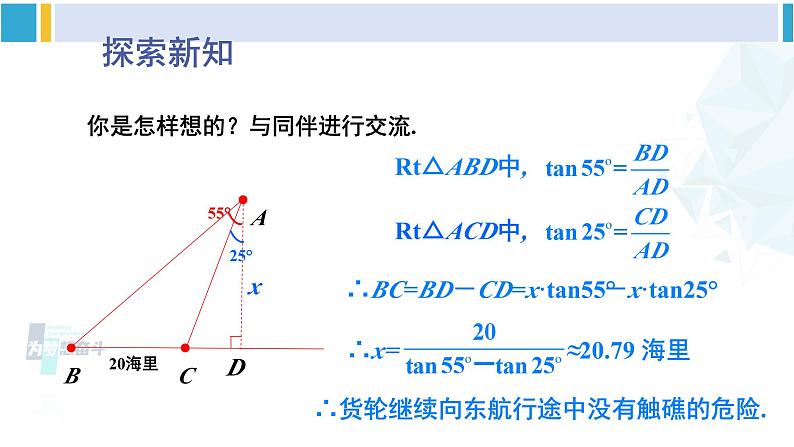
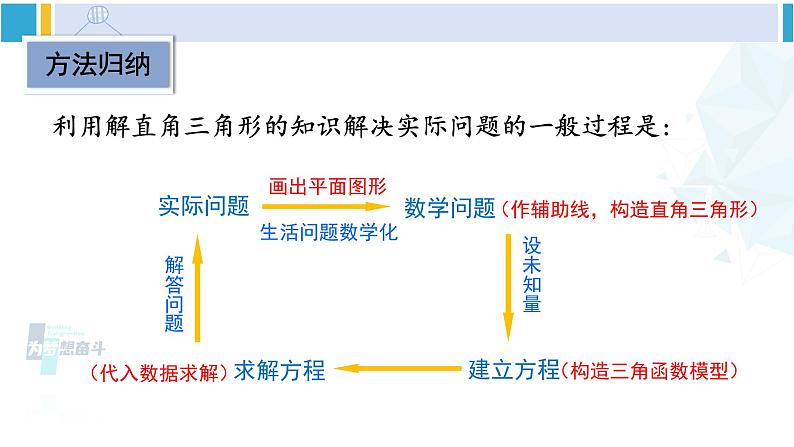
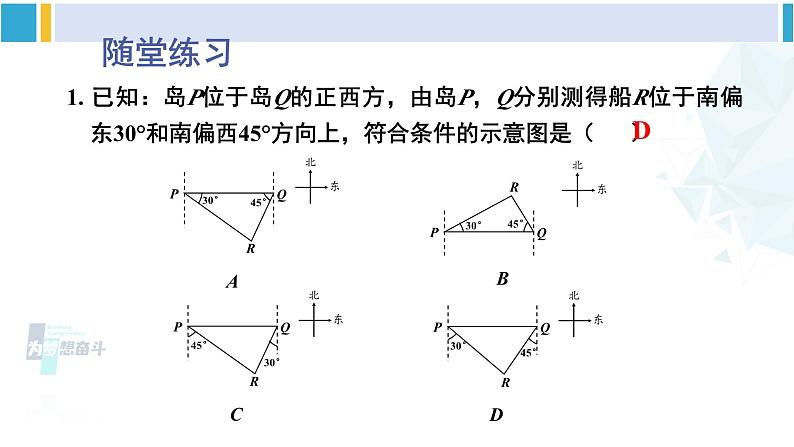
北师版·九年级下册5 三角函数的应用第1课时 方向角问题情景导入探索新知ABC25° 如图，海中有一个小岛A，该岛四周10海里内有暗礁.一货轮由西向东航行，开始在A岛南偏西55º的B处，往东行驶20海里后到达该岛的南偏西25º的C处.之后，货轮继续向东航行.你认为货轮继续向东航行途中会有触礁的危险吗？ 55°探索新知AB55°C25°你是怎样想的？与同伴进行交流.20海里D解: 过A点作BC的垂线AD，则AD的长即为货轮距离小岛的最短距离.若AD＞10海里，则货轮安全；反之则有触礁的危险.设AD=x.x探索新知AB55°C25°你是怎样想的？与同伴进行交流.20海里Dx Rt△ABD中, Rt△ACD中, ∴BC=BD－CD=x·tan55°－x·tan25° ∴x= ≈20.79 海里∴货轮继续向东航行途中没有触礁的危险.利用解直角三角形的知识解决实际问题的一般过程是: 实际问题画出平面图形生活问题数学化 数学问题（作辅助线，构造直角三角形）设未知量 建立方程（构造三角函数模型）（代入数据求解） 求解方程解答问题随堂练习1. 已知：岛P位于岛Q的正西方，由岛P，Q分别测得船R位于南偏东30°和南偏西45°方向上，符合条件的示意图是（ ）D2. 如图，一艘海轮位于灯塔P的北偏东55°方向，距离灯塔2海里的点A处.如果海轮沿正南方向航行到灯塔的正东方向，那么海轮航行的距离AB的长是（ ）A.2海里 B.2sin55°海里C.2cos55°海里 D.2tan55°海里PAB北55°2海里55°C3. 如图，C，D分别是某一湖的南、北两端A和B的正东方向的两个村庄，CD=6km，且D位于C的北偏东30°的方向上，则AB=_____ km .6km30°E4. [贺州中考]如图，在A处的正东方向有一港口B.某巡逻艇从A处沿着北偏东60°方向巡逻，到达C处时接到命令，立刻在C处沿东南方向以20n mile/h的速度行驶3h到达港口B.求A，B间的距离.（ ，结果精确到0.1 n mile ）北东ABC60°D解：如图所示，过点C作CD⊥AB，垂足为D，则∠ACD=60°，∠BCD=45°.在Rt△BCD中，4. [贺州中考]如图，在A处的正东方向有一港口B.某巡逻艇从A处沿着北偏东60°方向巡逻，到达C处时接到命令，立刻在C处沿东南方向以20n mile/h的速度行驶3h到达港口B.求A，B间的距离.（ ，结果精确到0.1 n mile ）北东AB60°D在Rt△ACD中，即A，B间的距离约为114.7n mile.C5. 如图，某同学在河东岸点A处测得河对岸边的一点C在A的北偏西31°的方向上，沿河岸向北前进21m到达B处，测得C在B的北偏西45°的方向上.请你根据以上数据，帮助该同学计算出这条河的宽度.（结果精确到0.1m.参考数据: sin 31°≈0.52，cos 31°≈ 0.86，tan31°≈ 0.60）31°21m45°D解：如图所示，过点C作CD⊥AB，垂足为D.设CD=x m.∵∠CBD=45°，∴CD=BD=x m.在Rt△ACD中，解得x=31.5故这条河的宽度约为31.5 m.课堂小结利用解直角三角形的知识解决实际问题的一般过程是:课后练习习题1.64