北师大版九年级数学下册 第三章 圆 3 垂径定理（课件）

这是一份北师大版九年级数学下册 第三章 圆 3 垂径定理（课件），共27页。
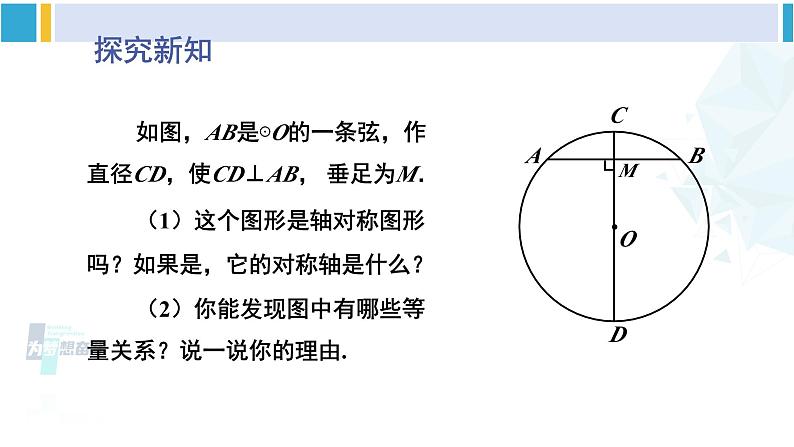
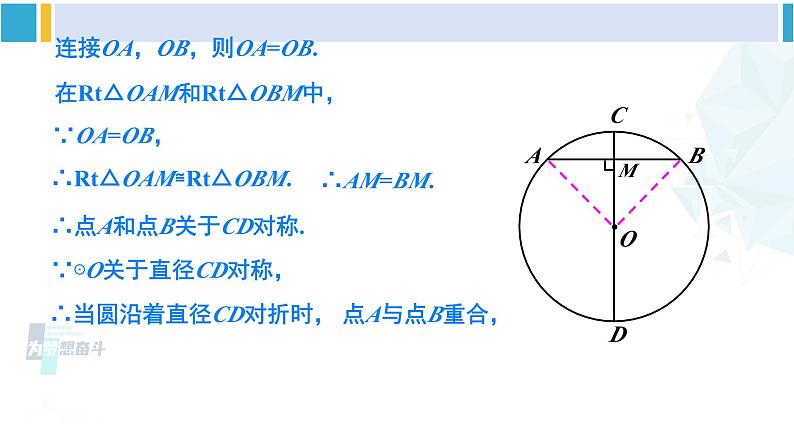
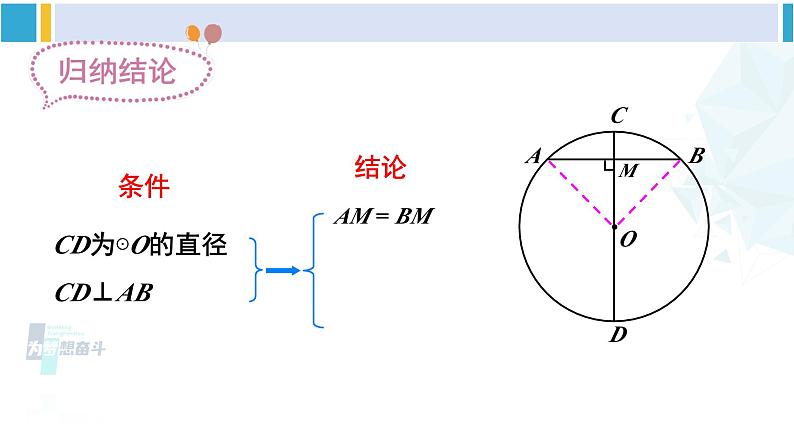
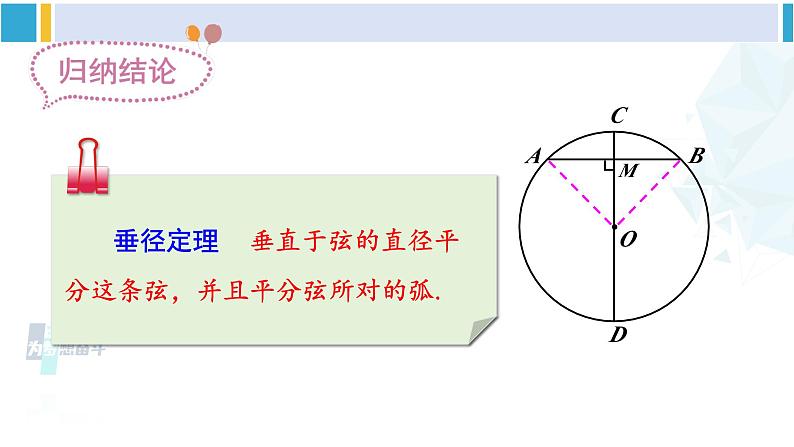
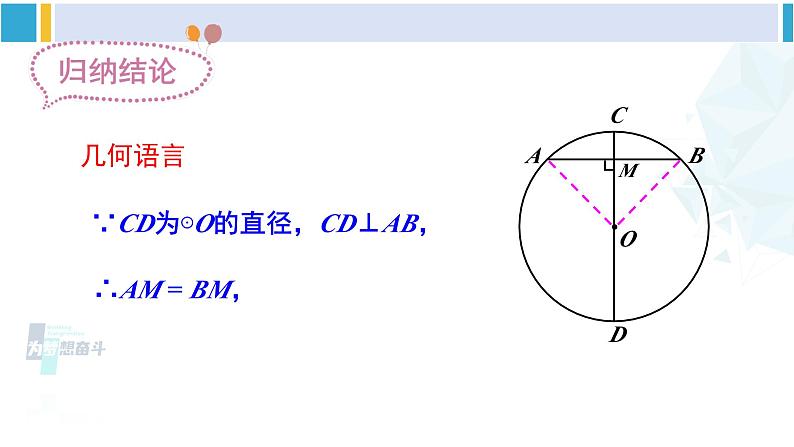
北师版·九年级下册3 垂径定理新课导入你知道赵州桥吗？它是1300多年前我国隋代建造的石拱桥，是我国古代人民勤劳与智慧的结晶．它的主桥是圆弧形，它的跨度（弧所对的弦的长）为37.4m，拱高（弧的中点到弦的距离）为7.2m，你能求出赵州桥主桥拱的半径吗？37.4m7.2m探究新知如图，AB是⊙O的一条弦，作直径CD，使CD⊥AB， 垂足为M．（1）这个图形是轴对称图形吗？如果是，它的对称轴是什么？（2）你能发现图中有哪些等量关系？说一说你的理由.连接OA，OB，则OA=OB.在Rt△OAM和Rt△OBM中，∵OA=OB，∴Rt△OAM≌Rt△OBM.∴AM=BM.∴点A和点B关于CD对称.∵⊙O关于直径CD对称，∴当圆沿着直径CD对折时， 点A与点B重合，垂径定理 垂直于弦的直径平分这条弦，并且平分弦所对的弧.几何语言∵CD为⊙O的直径，CD⊥AB， 判断下列图形，能否使用垂径定理？定理中的两个条件缺一不可——直径（半径），垂直于弦如图，AB 是⊙O 的弦（不是直径），作一条平分 AB 的直径 CD，交 AB 于点 M ．（1）这个图形是轴对称图形吗？如果是，它的对称轴是什么？（2）你能发现图中有哪些等量关系？说一说你的理由.CD⊥ABAM = BM理由是：连接OA，OB，则OA=OB.在△OAM和△OBM中，∵ OA=OB，AM=BM.∴ △OAM≌△OBM.∴ ∠AMO=∠BMO.∴ CD⊥AB∵ ⊙O关于直径CD对称，∴ 当圆沿着直径CD对折时，点A与点B重合， 平分弦 的直径垂直于弦，并且平分弦所对的弧．（不是直径）垂径定理的逆定理几何语言∵CD为⊙O的直径， AM = BM，还有如下正确结论：根据垂径定理与推论可知对于一个圆和一条直线来说，如果具备（1）过圆心；（2）垂直于弦；（3）平分弦；（4）平分弦所对的优弧；（5）平分弦所对的劣弧.上述五个条件中的任何两个条件都可以推出其他三个结论.解：连接 OC .设弯路的半径为 R m，则 OF =（R – 90）m .∵ OE⊥CD ，∴ 在Rt△OCF 中，根据勾股定理， 得 OC2 = CF2 + OF2，即R2 = 3002 +（R – 90）2.解这个方程，得 R = 545.所以，这段弯路的半径为 545 m.随堂练习D垂径定理 垂直于弦的直径平分这条弦，并且平分弦所对的弧.勾股定理123. 赵州桥主桥拱的跨度（弧所对的弦的长）为37.4m，拱高（弧的中点到弦的距离）为7.2m，你能求出赵州桥主桥拱的半径吗？再逛赵州石拱桥解：如图，OD = OC – DC = R – 7.2 .在 Rt△AOD 中，由勾股定理，得OA2 = AD2 + OD2 ，即 R2 = 18.72 +（R – 7.2）2解得 R ≈ 27.9（m）.答：赵州桥的主桥拱半径约为27.9m.AB = 37.4，CD = 7.24.如图所示，OC 交 AB 于点 D，AD = DB，AB = 6cm，CD = 1cm，求⊙O 的半径长.解：设圆的半径为 R，则OB = OC = R，∵ AD = DB，∴ OC⊥AB，根据勾股定理，得32+（R – 1）2 = R2，解得 R = 5 cm.即⊙O 的半径长为 5 cm.5. 如果圆的两条弦互相平行，那么这两条弦所夹的弧相等吗？为什么？ 圆心在平行弦外圆心在其中一条弦上圆心在平行弦内MN课堂小结课后作业习题3.31、2、3、4