2023年陕西省西安市未央区小升初数学试卷

这是一份2023年陕西省西安市未央区小升初数学试卷，共18页。试卷主要包含了认真读题，正确填空，仔细推敲，认真辨析，反复比较，慎重选择，一丝不苟，细心计算，按要求完成下面各题，灵活运用知识，解决下列问题等内容，欢迎下载使用。

1．（3分）某市新规划一条快速路，计划投资985069000元，横线上的数读作 ，改写成用“万”作单位的数是 万元，省略亿位后面的尾数约是 亿元。
2．（2分）24的因数有 个，10和12的最小公倍数是 。
3．（3分）在横线里填上合适的数。
3000平方米＝ 公顷
6.03平方米＝ 平方米 平方分米
4．（4分）＝＝7÷ ＝ %＝ （填小数）
5．（2分）一辆汽车时行驶20千米，这辆汽车行驶的路程和所用时间的比是 ，比值是 。
6．（2分）如图，每个小方格的面积是1cm。
（1）点C的位置用数对表示是 ；
（2）三角形的面积是 平方厘米。
7．（1分）昆虫爱好者发现某地蟋蟀叫的次数与气温之间有如下近似关系：t＝7h﹣21（t表示蟋蟀每分钟叫的次数，h表示当时的气温（℃））。根据这个式子，当蟋蟀每分钟叫189次时，当时气温达到 ℃。
8．（1分）单独完成一项工作，甲要4天，乙要5天，甲的工作效率比乙高 %。
9．（1分）一个圆锥形状的铅锤，底面半径是2厘米，高9厘米，把它没入盛满水的大烧杯里，将有 毫升的水溢出烧杯。
10．（2分）在如表中，当x与y成正比例时，“？”处应填 ；当x与y成反比例时，“？”处应填 。
11．（1分）将一个分数的分母减去2得．如果将它的分母加上1，则得，这个分数是 ．
12．（2分）用黑白两种颜色的正六边形地砖按图所示的方式排成若干个图案，第4个图案中有白色地砖 块，第n个图案中白色地砖 块。
二、仔细推敲，认真辨析。（对的画“√”，错的画“×”）（5分）
13．（1分）0是正数和负数的分界点。
14．（1分）王叔叔加工了103个零件，经严格检验，有100个合格，合格率是100%。
15．（1分）（a、b均不为0），则a＞b。
16．（1分）一个不透明的袋子里有2个红球和2个蓝球，每次摸出1个球后再放回，第一次摸出红球，所以第二次摸出蓝球的可能性大。
17．（1分）如果两个圆柱的侧面积相等，那么它们的体积也相等．
三、反复比较，慎重选择。（将正确答案的序号填在括号里）
18．（2分）奇奇想绘制统计图表示11月份各项家庭支出占总支出的百分比，他应选择（ ）
A．条形统计图B．扇形统计图
C．折线统计图D．复式折线统计图
19．（2分）在14×12的竖式中，箭头所指的这一步表示（ ）
A．10个14的和B．12个14的和
C．1个14D．无法确定
20．（2分）一幅图的比例尺是如果A、B两地相距300km，那么画在这幅图上应是（ ）cm。
A．25B．7.5C．75D．2.5
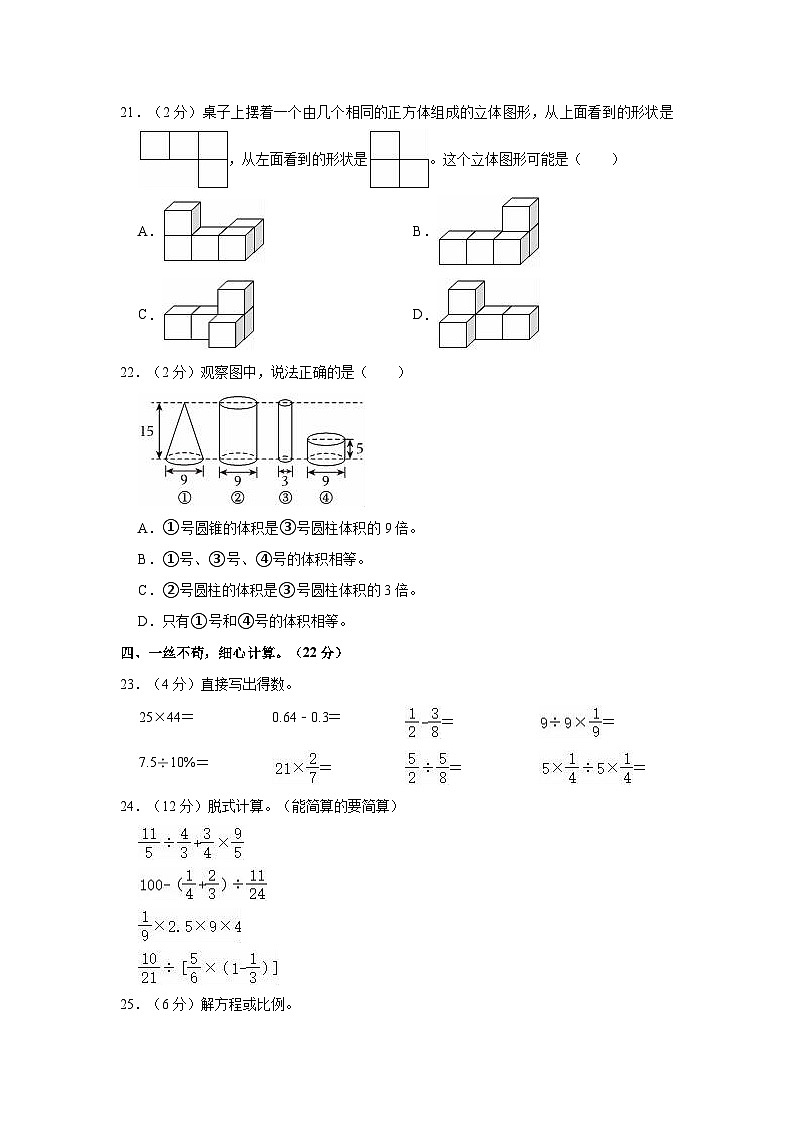
21．（2分）桌子上摆着一个由几个相同的正方体组成的立体图形，从上面看到的形状是，从左面看到的形状是。这个立体图形可能是（ ）
A．B．
C．D．
22．（2分）观察图中，说法正确的是（ ）
A．①号圆锥的体积是③号圆柱体积的9倍。
B．①号、③号、④号的体积相等。
C．②号圆柱的体积是③号圆柱体积的3倍。
D．只有①号和④号的体积相等。
四、一丝不苟，细心计算。（22分）
23．（4分）直接写出得数。
24．（12分）脱式计算。（能简算的要简算）
25．（6分）解方程或比例。
1.2x+2x＝4.8
五、按要求完成下面各题。（14分）
26．（4分）在方格纸上按要求画图。
（1）画出图形①向右平移5格后的图形。
（2）画出图形②绕点O顺时针旋转90°后的图形。
27．（3分）（1）学校在中心广场北偏西60°方向600m处，这幅图的比例尺是 。
（2）书店在中心广场南偏东50°方向900m处，请在图中用“•”标出书店的位置。
28．（7分）大数据与行业融合是产业发展的重要方向。某服装公司通过大数据得知A、B两款品牌服装2018～2022年“六一”期间的销售情况，并制作了如图所示统计图。
（1）A、B两款品牌服装 年“六一”期间销售额相同， 年销售额相差最大。
（2）2019年“六一”期间，B款品牌服装比A款品牌服装销售额少 %。
（3）按照图中趋势，2023年“六一”期间B款品牌服装的销售额大约会是 万元，我这样想： 。
（4）如果你是销售顾问，请根据图中数据，对A款品牌服装提出建议。
六、灵活运用知识，解决下列问题。（25分）
29．（5分）某方便面的广告语这样说：“赠量25%，加量不加价．”一袋方便面现在的重量是120克，你知道赠量前是多少克吗？
30．（5分）红叶服装厂生产一批校服，第一周生产了全部的，第二周生产了900件，这时已经生产的占全部的，这批校服共有多少件？
31．（5分）一颗人造地球卫星，在空中绕地球6周需要10.6小时，照这样的速度，运行15周需要多少小时？（列比例解答）
32．（5分）实验小学组织同学们开展“航天梦”主题绘画比赛。其中四、五、六年级共有180人参加这次绘画比赛，四年级参加的人数占三个年级总人数的，五年级和六年级参赛的人数比是2：3，六年级参加绘画比赛的有多少人？
33．（5分）下面是一个零件的示意图（单位：厘米），它是由一个长方体从前往后挖掉（挖通）一个底面直径为10厘米的圆柱体得到的，求这个零件的体积。（π取3.14）
2023年陕西省西安市未央区小升初数学试卷
参考答案与试题解析
一、认真读题，正确填空。（每空1分，共24分）
1．【分析】根据整数的读法：从高位到低位，一级一级地读，每一级末尾的0都不读出来，其它数位连续几个0都只读一个零，即可读出此数；把不是整万的数改成以“万”为单位的数时，就是把整数的小数点向左移动四位点上小数点，然后在后面加上“万”字；省略“亿”后面的尾数就是四舍五入到亿位，即把亿位后面的千万位上的数进行四舍五入，再在数的后面写上“亿”字。
【解答】解：985069000 读作；九亿八千五百零六万九千；
985069000＝98506.9万；
985069000≈10亿。
故答案为：九亿八千五百零六万九千，98506.9，10。
【点评】本题主要考查整数的读法、改写和求近似数，注意改写和求近似数时要带计数单位。
2．【分析】找配对，24＝1×24＝2×12＝3×8＝4×6，据此写出答案；
先把10和12分解质因数，再把它们一切公有的质因数和其中几个数公有的质因数以及每个数的独有的质因数全部连乘起来，所得的积就是它们的最小公倍数。
【解答】解：24＝1×24＝2×12＝3×8＝4×6
24的因数有：1、2、3、4、6、8、12、24共有8个；
10＝2×5
12＝2×2×3
10和12的最小公倍数是2×5×2×3＝60。
故答案为：8；60。
【点评】本题考查的是找一个数的因数和求几个数的最小公倍数，关键是找一个数的因数可以用找配对即哪两个因数相乘得这个数；两个数的公有质因数与每个数独有质因数的连乘积是最小公倍数，数字大的可以用短除法解答。
3．【分析】根据1公顷＝10000平方米，1平方米＝100平方分米，解答此题即可。
【解答】解：3000平方米＝0.3公顷
6.03平方米＝6平方米3平方分米
故答案为：0.3；6；3。
【点评】熟练掌握面积单位的换算，是解答此题的关键。
4．【分析】根据分数的基本性质，分数的分子和分母同时乘或除以相同的数（0除外），分数大小不变，转化成需要的分数；分数的分子作为被除数，分母作为除数，根据商不变的性质，被除数和除数同时乘或除以相同的数（0除外），商不变；用分子除以分母转化成小数；最后由小数转化成百分数，将小数乘100，得到12.5，然后在后面加上百分号，即12.5%。
【解答】解：＝＝
＝1÷8＝（1×7）÷（8×7）＝7÷56
＝0.125＝12.5%
则＝＝7÷56＝12.5%＝0.125。
故答案为：5，56，12.5，0.125。
【点评】此题考查了小数、分数和百分数之间的关系及其转化，要求学生能够掌握。
5．【分析】先求出这辆汽车行驶的路程和所用时间的比，然后化成最简整数比；再用前项除以后项，求出比值即可。
【解答】解：20：
＝（20×2）：（×2）
＝40：1
40÷1＝40
答：这辆汽车行驶的路程和所用时间的比是40：1，比值是40。
故答案为：40：1；40。
【点评】解答本题需熟练掌握比的意义、化简比及求比值的方法，灵活解答。
6．【分析】（1）C点在第4列，第2行；
（2）根据三角形面积公式可得。
【解答】解：根据分析可得，（1）点C的位置用数对表示是 （4，2）；
（2）2×3÷2＝3（厘米2）
故答案为：（4，2），3。
【点评】本题考查了学生对用数对表示位置的方法的掌握，及三角形面积公式的灵活应用。
7．【分析】将t＝189代入关系式t＝7h﹣21，解关于h的方程即可。
【解答】解：将t＝189代入关系式t＝7h﹣21，得：
189＝7h﹣21
7h﹣21+21＝189+21
7h＝210
7h÷7＝210÷7
h＝30
答：当蟋蟀每分钟叫189次时，当时气温达到30℃。
故答案为：30。
【点评】此题主要考查了含有字母的算式的求值问题，采用代入法即可。
8．【分析】把这件工作看作单位“1”，首先根据“工作效率＝工作量÷工作时间”，分别求出甲、乙的工作效率，再根据求一个数比另一个数少百分之几的计算方法，求出甲的工作效率比乙的工作效率高的部分，再除以乙的工作效率即可。
【解答】解：1÷4＝
1÷5＝
（﹣）÷
＝÷
＝25%
答：甲的工作效率比乙高25%。
故答案为：25。
【点评】此题考查的目的是理解掌握工作量、工作效率、工作时间三者之间的关系以及百分数应用题相关的应用。
9．【分析】根据题意可知：溢出水的体积等于圆锥铅锥的体积，根据圆锥的体积公式：V＝Sh，把数据代入公式解答。
【解答】解：×3.14×22×9
＝12.56×9
＝37.68（立方厘米）
37.68立方厘米＝37.68毫升
答：将有37.68毫升的水溢出烧杯。
故答案为：37.68。
【点评】此题主要考查圆锥体积公式的灵活运用。
10．【分析】根据正、反比例的意义列关于“？”的方程：正比例关系可以用式子表示为：＝k（一定），所以＝，据此求出如果表中的x与y成正比例，那么表中的括号应填的数；然后根据反比例关系可以用式子表示为：xy＝m（一定），所以12x＝9×6，据此求出如果表中的x与y成反比例，那么表中的括号应填多少即可。
【解答】解：若x与y成正比例关系，则：
＝
9x＝6×12
9x＝72
9x÷9＝72÷9
x＝8
若x与y成反比例关系，则：
12x＝9×6
12x＝54
12x÷12＝54÷12
x＝4.5
答：当x与y成正比例时，“？”处应填8；当x与y成反比例时，“？”处应填4.5。
故答案为：8，4.5。
【点评】本题考查了利用正、反比例解决问题。若两种相关联的量成正比例，则其比值一定；若两种相关联的量成反比例，则其乘积一定。
11．【分析】根据题意可知：两次都是改变分数的分母，没有改变分数的分子，这样运算的结果就出现了两次，即一次是，另一次是；现将这两个分数通分，可分别得和，但不符合分子相等的题意，所以可以把化成与分子相同的分数为；进而设原来的分母是x，那么就有x﹣2＝15，x+1＝18，解答x＝17，所以原来的分数就是．
【解答】解：＝，＝，不符合分子相等的题意
把化成与分子相同的分数，即＝
设原分母为x，由题意得
x﹣2＝15或x+1＝18，解得x＝17
所以原分数是．
故答案为：．
【点评】解决此题关键是根据题意，先求出原来分数分子的数值，进而求得分母的数值．
12．【分析】第1个图案中有白色地砖6块，即4×1+2；
第2个图案中有白色地砖10块，即4×2+2；
第3个图案中有白色地砖14块，即4×3+2；
……
第n个图案中有白色地砖的块数为：4n+2。
【解答】解：由分析可知，第n个图案中有白色地砖的块数为：（4n+2）块。
当n＝4时，
4×4+2
＝16+2
＝18（块）
答：第4个图案中有白色地砖18块，第n个图案中白色地砖（4n+2）块。
故答案为：18，（4n+2）。
【点评】本题主要考查数与形结合的规律，发现每多1个图形就多4块白色地砖是解本题的关键。
二、仔细推敲，认真辨析。（对的画“√”，错的画“×”）（5分）
13．【分析】0既不正数，也不是负数，它是正数与负数的分界点。
【解答】解：0是正数和负数的分界点，这种说法是正确的。
故答案为：√。
【点评】这道题考查的是正负数的知识，要知道“0是正数和负数的分界点”。
14．【分析】明确合格率，合格率指的是合格零件数是生产零件总数的百分之几，根据公式：合格率＝×100%。
【解答】解：
所以本题说法错误。
故答案为：×
【点评】本题考查合格率的计算。运用合格率＝×100%进行解答即可。
15．【分析】假设×a＝×b＝1，分别求出a、b的值，然后比较即可解答。
【解答】解：假设×a＝×b＝1。
×a＝1
a＝1÷
a＝
×b＝1
b＝1÷
b＝
＞，所以a＞b。
则（a、b均不为0），则a＞b。故原说法正确。
故答案为：√。
【点评】此题考查了分数大小的比较，要求学生掌握。
16．【分析】每次摸出1个球后再放回，第二次摸的时候，袋子里也是有2个红球和2个蓝球，摸到红球、蓝球的可能性一样大。
【解答】解：第二次，摸到红球、蓝球的可能性一样大。
故答案为：×。
【点评】本题的关键是知道怎样判断可能性的大小，与红球、蓝球的数量有关，与上一次的结果没有关系。
17．【分析】圆柱的体积＝底面积×高，圆柱的侧面积＝底面周长×高，因为它们的侧面面积相等，但底面半径和高不一定相等，所以体积也不一定相等，据此即可解答．
【解答】解：因为圆柱的体积＝底面积×高，圆柱的侧面积＝底面周长×高，
因为它们的侧面面积相等，仅仅说明底面周长和高的积相等，但底面半径和高不一定相等，
所以体积也不一定相等，
故答案为：×．
【点评】解答此题的主要依据是：圆柱的侧面积以及体积的计算方法．
三、反复比较，慎重选择。（将正确答案的序号填在括号里）
18．【分析】条形统计图能很容易看出数量的多少；折线统计图不仅容易看出数量的多少，而且能反映数量的增减变化情况；扇形统计图能反映部分与整体的关系；由此根据情况选择即可。
【解答】解：奇奇想绘制统计图表示11月份各项家庭支出占总支出的百分比，他应选择扇形统计图。
故选：B。
【点评】此题应根据条形统计图、折线统计图、扇形统计图各自的特点进行解答。
19．【分析】“14”即140，是由14和10相乘所得，表示10个14的和是140。
【解答】解：14×10＝140
箭头所指的这一步表示10个14的和。
故选：A。
【点评】本题主要考查了两位数乘两位数乘法的竖式计算方法，明确各步的意义是解答本题的关键。
20．【分析】根据线段比例尺的意义，可知表示图上1厘米代表实际距离40千米，用（300÷40）即可求得图上距离。
【解答】解：300÷40＝7.5（厘米）
答：画在这幅图上应是7.5cm。
故选：B。
【点评】本题主要考查线段比例尺的意义，结合题意分析解答即可。
21．【分析】根据观察物体的方法，分别分析各个选项中的图形从上面和左面看到的形状，结合题意解答即可。
【解答】解：从上面看到的形状是，从左面看到的形状是。
故选：C。
【点评】本题是考查从不同方向观察物体和几何图形，培养学生的观察能力和空间想象能力。
22．【分析】因为等底等高的用的体积是圆锥体积的3倍，所以当圆柱与圆锥的体积相等，底面积也相等时，圆柱的高是圆锥高的。据此解答即可。
【解答】解：15×＝5
所以只有①号和④号的体积相等。
故选：D。
【点评】此题考查的目的是理解掌握等底等高的圆柱与圆锥体积之间的关系及应用。
四、一丝不苟，细心计算。（22分）
23．【分析】根据整数、小数、分数、百分数加减乘除法以及四则混合运算的顺序，直接进行口算即可。
【解答】解：
【点评】本题考查了简单的计算，计算时要细心，注意平时积累经验，提高计算的水平。
24．【分析】第一题先把除法转化成乘法，再根据乘法分配律简算；第二题先算小括号里的加法，再算小括号外的除法，最后算小括号外的减法；第三题根据乘法交换律和结合律简算；第四题先算小括号里的减法，再算中括号里的乘法，最后算中括号外的除法。
【解答】解：÷+×
＝×+×
＝（+）×
＝4×
＝3
100﹣（+）÷
＝100﹣÷
＝100﹣2
＝98
×2.5×9×4
＝（×9）×（2.5×4）
＝1×10
＝10
÷[×（1﹣）]
＝÷[×]
＝÷
＝
【点评】此题主要考查分数、小数的四则混合运算的运算顺序和应用运算定律进行简便计算。
25．【分析】（1）先把方程左边化简为3.2x，两边再同时除以3.2；
（2）先把方程左边化简为0.25x，两边再同时除以0.25；
（3）根据比例的基本性质，先把比例化为方程，两边再同时乘3。
【解答】解：（1）1.2x+2x＝4.8
3.2x＝4.8
3.2x÷3.2＝4.8÷3.2
x＝1.5
（2）x﹣75%x＝
0.25x＝
0.25x÷0.25＝÷0.25
x＝
（3）
x＝
3×x＝
x＝
【点评】熟练掌握等式的基本性质和比例的基本性质是解题的关键。
五、按要求完成下面各题。（14分）
26．【分析】（1）根据平移的特征，把图形①的四个顶点分别向右平移5格，再首尾连接各点即可；
（2）把图形②与O点相连的两边分别绕点O沿顺时针方向旋转90°后，再把对角线绕点O沿顺时针方向旋转90°后连线即可。
【解答】解：由分析可得，。
【点评】此题重点考查平移与旋转的应用，作图时要选取关键点解决问题。
27．【分析】（1）用图上距离和实际距离的比化成前项是1的比，即是比例尺；
（2）先实际距离除以比例尺，求出图上距离，再根据给的角度和方向画图。
【解答】解：（1）2cm：600m＝2：60000＝1：30000
所以这幅图的比例尺是1：30000；
（2）900m＝90000cm
90000×＝3（cm）
。
故答案为：1：30000。
【点评】此题主要考查依据方向（角度）和距离判定物体位置的方法以及比例尺的意义，关机键是根据图上距离和实际距离求出比例尺，再根据比例尺和实际距离，求出图上距离，结合所给的角度和方向，画图确定位置。
28．【分析】（1）从统计表上可得，2020年两个品牌的销售额相同为45万元，在2022年两个品牌销售额相差最大，相差40万元。
（2）先算出两个品牌在2019销售额相差多少，再除以A的销售额即可得出答案。
（3）本题为开放性题目，言之有理即可，答案不唯一。
（4）本题为开放性题目，言之有理即可，答案不唯一。
【解答】解：（1）A、B两款品牌服装2020年“六一”期间销售额相同，2022年销售额相差最大。
（2）（50﹣30）÷50×100%
＝20÷50×100%
＝0.4×100%
＝40%
答：B款品牌服装比A款品牌服装销售额少40%。
（3）按照图中趋势，2023年B款品牌服装的销售额大约会是80万元，我这样想：从统计表上的，B款的每年增长10万元左右，所以我预计2023年B款品牌服装的销售额大约会是80万元。（答案不唯一）
（4）对A款品牌服装提出建议可对市场进行调研，分析销售额下降的原因，并进行改进。（答案不唯一）
故答案为：2020，2022；40；80，从统计表上的，B款的每年增长10万元左右，所以我预计2023年B款品牌服装的销售额大约会是80万元。（答案不唯一）。
【点评】本题考查学生对复式折线统计图的掌握和运用。
六、灵活运用知识，解决下列问题。（25分）
29．【分析】把赠量前的质量看作单位“1”，120就相当于单位“1”的（1+25%），求单位“1”用除法计算，列式为：120÷（1+25%），据此解答．
【解答】解：120÷（1+25%），
＝120÷，
＝96（克）；
答：赠量前是96克．
【点评】此题是较简单的分数除法应用题，关键是找到数量对应的分率，然后再根据“已知一个数的几分之几是多少，求这个数用除法”列式解答．
30．【分析】把这批校服的总件数看作单位“1”，则第二周生产的件数占总件数的（﹣），已知第二周生产了900件，用900除以第二周生产的件数占总件数的分率，即可求出这批校服共有多少件。
【解答】解：900÷（﹣）
＝900÷
＝3000（件）
答：这批校服共有3000件。
【点评】解答本题的关键是求出第二周生产的件数占总件数的分率。
31．【分析】照这样的速度是指运行一周需要的时间是一定的。因为总时间÷周数＝运行一周需要的时间（一定），所以总时间和周数成正比例关系，据此列比例解答。
【解答】解：设运行15周要用x小时。
10.6：6＝x：15
6x＝10.6×15
6x＝159
x＝26.5
答：运行15周要用26.5小时。
【点评】解答此题的关键是：先判断题中的两种相关联的量成什么比例，并找准对应量。
32．【分析】根据题意，因为四年级参加的人数占三个年级总人数的，那么五六年级占三个年级总数的（1﹣），利用总人数乘此分率即可求出五六年级的总人数，再按2：3进行比例分配即可。
【解答】解：180×（1﹣）
＝180×
＝150（人）
2+3＝5
答：六年级参加绘画比赛的有90人。
【点评】解答此题的关键是求出五六年级的总人数再进行比例分配。
33．【分析】通过观察图形可知，这个零件的体积等于长方体的体积减去圆柱的体积，根据长方体的体积公式：V＝abh，圆柱的体积公式：V＝πr2h，把数据代入公式解答。
【解答】解：30×5×20﹣3.14×（10÷2）2×5
＝150×20﹣3.14×25×5
＝3000﹣392.5
＝2607.5（立方厘米）
答：这个零件的体积是2607.5立方厘米。
【点评】此题主要考查长方体的体积公式、圆柱的体积公式的灵活运用，关键是熟记公式。
x
6
？
y
9
12
25×44＝
0.64﹣0.3＝
＝
＝
7.5÷10%＝
＝
＝
＝
25×44＝1100
0.64﹣0.3＝0.34
＝
＝
7.5÷10%＝75
＝6
＝4
＝