北师大版七年级下册第一章 整式的乘除6 完全平方公式课前预习课件ppt

这是一份北师大版七年级下册第一章 整式的乘除6 完全平方公式课前预习课件ppt，共18页。PPT课件主要包含了教学目标，新课导入，情景导入，你发现了什么，p2+2p+1，m2+4m+4，p2-2p+1，m2-4m+4，a2+2ab+b2，a2-2ab+b2等内容，欢迎下载使用。
1.理解并掌握完全平方公式的推导过程、结构特点、几何解释.（重点）2.运用完全平方公式进行计算.（难点）
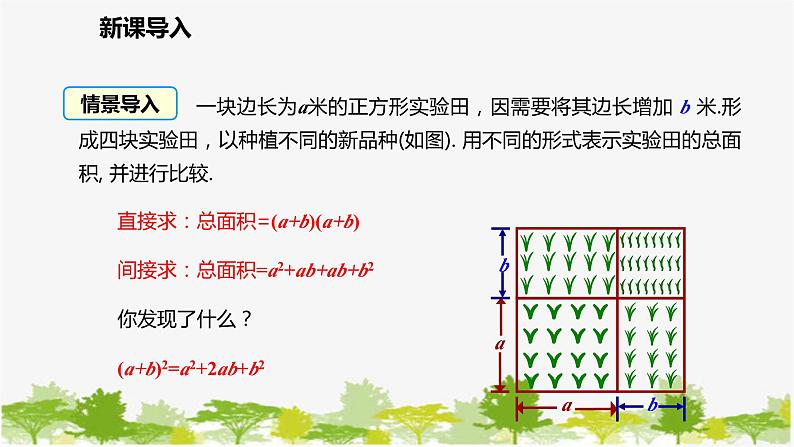
一块边长为a米的正方形实验田，因需要将其边长增加 b 米.形成四块实验田，以种植不同的新品种(如图). 用不同的形式表示实验田的总面积, 并进行比较.
直接求：总面积=(a+b)(a+b)
间接求：总面积=a2+ab+ab+b2
(a+b)2=a2+2ab+b2
问题1 计算下列多项式的积，你能发现什么规律？
（1） (p+1)2=(p+1)(p+1)= ；
（2） (m+2)2=(m+2)(m+2)= ；
（3） (p-1)2=(p-1)(p-1)= ；
（4） (m-2)2=(m-2)(m-2)= .
问题2 根据你发现的规律，你能写出下列式子的答案吗？
(a+b)2= .
(a-b)2= .
也就是说，两个数的和（或差）的平方，等于它们的平方和，加上（或减去）它们的积的2倍.这两个公式叫做（乘法的）完全平方公式.
简记为：“首平方，尾平方，积的2倍放中央”
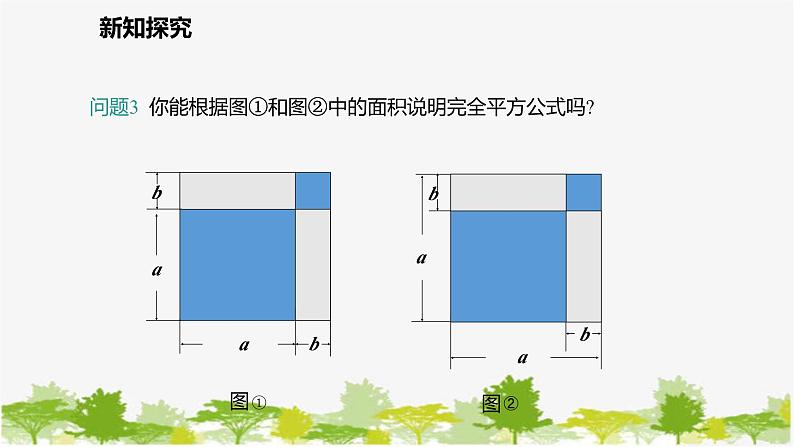
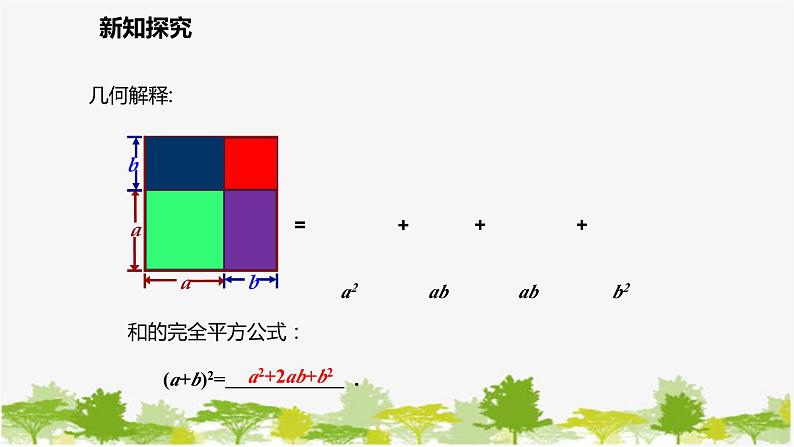
问题3 你能根据图①和图②中的面积说明完全平方公式吗?
(a+b)2= a2+2ab+b2.
(a-b)2= a2-2ab+b2.
问题4 观察下面两个完全平方式，比一比，回答下列问题：
1.说一说积的次数和项数.
2.两个完全平方式的积有相同的项吗？与a,b有什么关系？
3.两个完全平方式的积中不同的是哪一项？与 a,b有什么关系？它的符号与什么有关？
4.公式中的字母a，b可以表示数，单项式和多项式.
2.积中两项为两数的平方和；
3.另一项是两数积的2倍，且与两数中间的符号相同；
想一想：下面各式的计算是否正确？如果不正确,应当怎样改正？
(1)(x+y)2=x2 +y2；
(2)(x -y)2 =x2 -y2；
(3) (-x +y)2 =x2+2xy +y2；
(4) (2x+y)2 =4x2 +2xy +y2.
(x +y)2 =x2+2xy +y2
(x -y)2 =x2 -2xy +y2
(-x +y)2 =x2 -2xy +y2
(2x +y)2 =4x2+4xy +y2
运用完全平方公式计算：
解: (4m+n)2=
(1)(4m+n)2；
(a + b)2= a2 + 2ab + b2
(a - b)2 = a2 - 2 ab + b2
1. 利用完全平方公式计算：(1)(5－a)2； (2)(－3m－4n)2； (3)(－3a＋b)2.
(3)(－3a＋b)2＝9a2－6ab＋b2.
解：(1)(5－a)2＝25－10a＋a2.
(2)(－3m－4n)2＝9m2＋24mn＋16n2.
2. 利用平方差公式计算：
(1) ( x + 2y )( x – 2y) =______ ; (2) (– x+y)(– x – y)=______ ;(3) (mn – 3)(mn +3)= ______ ;(4) (– 2x+y)(2x+y)= ______ .
(a±b)2= a2 ±2ab+b2
2.下列计算结果为2ab－a2－b2的是( ) A．(a－b)2 B．(－a－b)2 C．－(a＋b)2 D．－(a－b)2
1.运用乘法公式计算(a-2)2的结果是（　　） A．a2-4a+4 B．a2-2a+4 C．a2-4 D．a2-4a-4